Multiresolution local smoothness detection in non-uniformly sampled multivariate signals

Inspired by edge detection based on the decay behavior of wavelet coefficients, we introduce a (near) linear-time algorithm for detecting the local regularity in non-uniformly sampled multivariate signals. Our approach quantifies regularity within the framework of microlocal spaces introduced by Jaffard. The central tool in our analysis is the fast samplet transform, a distributional wavelet transform tailored to scattered data. We establish a connection between the decay of samplet coefficients and the pointwise regularity of multivariate signals. As a by product, we derive decay estimates for functions belonging to classical H\"older spaces and Sobolev-Slobodeckij spaces. While traditional wavelets are effective for regularity detection in low-dimensional structured data, samplets demonstrate robust performance even for higher dimensional and scattered data. To illustrate our theoretical findings, we present extensive numerical studies detecting local regularity of one-, two- and three-dimensional signals, ranging from non-uniformly sampled time series over image segmentation to edge detection in point clouds.

Construction of generalized samplets in Banach spaces

Recently, samplets have been introduced as localized discrete signed measures which are tailored to an underlying data set. Samplets exhibit vanishing moments, i.e., their measure integrals vanish for all polynomials up to a certain degree, which allows for feature detection and data compression. In the present article, we extend the different construction steps of samplets to functionals in Banach spaces more general than point evaluations. To obtain stable representations, we assume that these functionals form frames with square-summable coefficients or even Riesz bases with square-summable coefficients. In either case, the corresponding analysis operator is injective and we obtain samplet bases with the desired properties by means of constructing an isometry of the analysis operator's image. Making the assumption that the dual of the Banach space under consideration is imbedded into the space of compactly supported distributions, the multilevel hierarchy for the generalized samplet construction is obtained by spectral clustering of a similarity graph for the functionals' supports. Based on this multilevel hierarchy, generalized samplets exhibit vanishing moments with respect to a given set of primitives within the Banach space. We derive an abstract localization result for the generalized samplet coefficients with respect to the samplets' support sizes and the approximability of the Banach space elements by the chosen primitives. Finally, we present three examples showcasing the generalized samplet framework.

On Quasi-Localized Dual Pairs in Reproducing Kernel Hilbert Spaces

In scattered data approximation, the span of a finite number of translates of a chosen radial basis function is used as approximation space and the basis of translates is used for representing the approximate. However, this natural choice is by no means mandatory and different choices, like, for example, the Lagrange basis, are possible and might offer additional features. In this article, we discuss different alternatives together with their canonical duals. We study a localized version of the Lagrange basis, localized orthogonal bases, such as the Newton basis, and multiresolution versions thereof, constructed by means of samplets. We argue that the choice of orthogonal bases is particularly useful as they lead to symmetric preconditioners. All bases under consideration are compared numerically to illustrate their feasibility for scattered data approximation. We provide benchmark experiments in two spatial dimensions and consider the reconstruction of an implicit surface as a relevant application from computer graphics.

Observation-specific explanations through scattered data approximation

This work introduces the definition of observation-specific explanations to assign a score to each data point proportional to its importance in the definition of the prediction process. Such explanations involve the identification of the most influential observations for the black-box model of interest. The proposed method involves estimating these explanations by constructing a surrogate model through scattered data approximation utilizing the orthogonal matching pursuit algorithm. The proposed approach is validated on both simulated and real-world datasets.

Fast Empirical Scenarios

We seek to extract a small number of representative scenarios from large and high-dimensional panel data that are consistent with sample moments. Among two novel algorithms, the first identifies scenarios that have not been observed before, and comes with a scenario-based representation of covariance matrices. The second proposal picks important data points from states of the world that have already realized, and are consistent with higher-order sample moment information. Both algorithms are efficient to compute, and lend themselves to consistent scenario-based modeling and high-dimensional numerical integration. Extensive numerical benchmarking studies and an application in portfolio optimization favor the proposed algorithms.

Samplet basis pursuit

We consider kernel-based learning in samplet coordinates with l1-regularization. The application of an l1-regularization term enforces sparsity of the coefficients with respect to the samplet basis. Therefore, we call this approach samplet basis pursuit. Samplets are wavelet-type signed measures, which are tailored to scattered data. They provide similar properties as wavelets in terms of localization, multiresolution analysis, and data compression. The class of signals that can sparsely be represented in a samplet basis is considerably larger than the class of signals which exhibit a sparse representation in the single-scale basis. In particular, every signal that can be represented by the superposition of only a few features of the canonical feature map is also sparse in samplet coordinates. We propose the efficient solution of the problem under consideration by combining soft-shrinkage with the semi-smooth Newton method and compare the approach to the fast iterative shrinkage thresholding algorithm. We present numerical benchmarks as well as applications to surface reconstruction from noisy data and to the reconstruction of temperature data using a dictionary of multiple kernels.

Anisotropic multiresolution analyses for deepfake detection

Generative Adversarial Networks (GANs) have paved the path towards entirely new media generation capabilities at the forefront of image, video, and audio synthesis. However, they can also be misused and abused to fabricate elaborate lies, capable of stirring up the public debate. The threat posed by GANs has sparked the need to discern between genuine content and fabricated one. Previous studies have tackled this task by using classical machine learning techniques, such as k-nearest neighbours and eigenfaces, which unfortunately did not prove very effective. Subsequent methods have focused on leveraging on frequency decompositions, i.e., discrete cosine transform, wavelets, and wavelet packets, to preprocess the input features for classifiers. However, existing approaches only rely on isotropic transformations. We argue that, since GANs primarily utilize isotropic convolutions to generate their output, they leave clear traces, their fingerprint, in the coefficient distribution on sub-bands extracted by anisotropic transformations. We employ the fully separable wavelet transform and multiwavelets to obtain the anisotropic features to feed to standard CNN classifiers. Lastly, we find the fully separable transform capable of improving the state-of-the-art.

Adaptive joint distribution learning

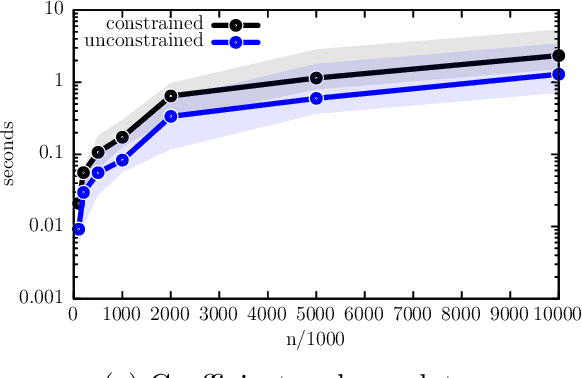
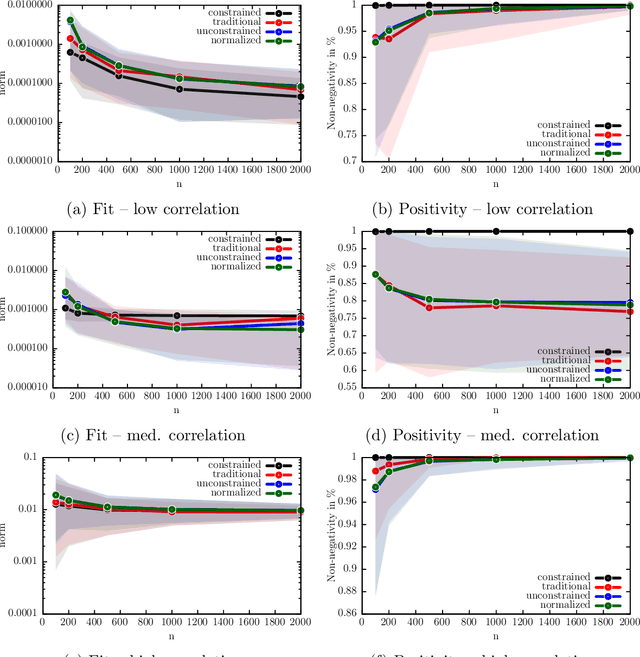
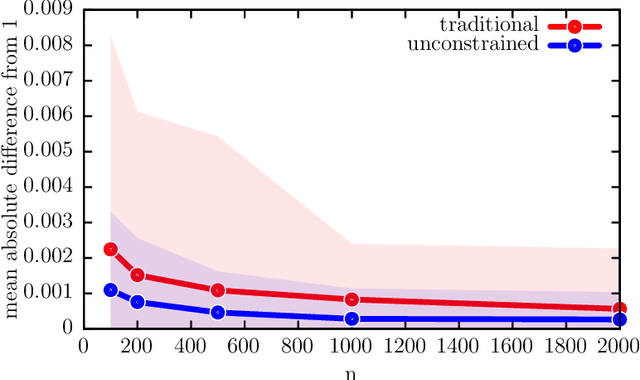
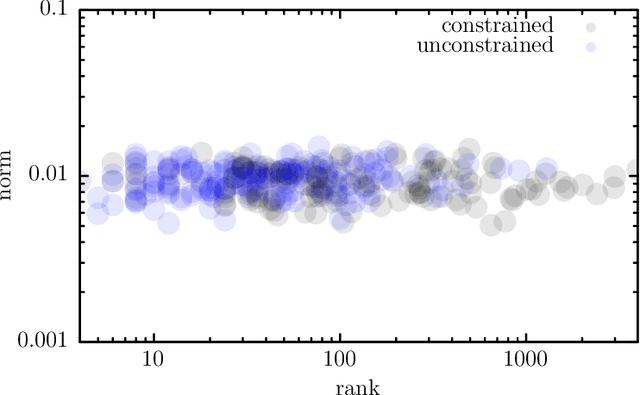
We develop a new framework for embedding (joint) probability distributions in tensor product reproducing kernel Hilbert spaces (RKHS). This framework accommodates a low-dimensional, positive, and normalized model of a Radon-Nikodym derivative, estimated from sample sizes of up to several million data points, alleviating the inherent limitations of RKHS modeling. Well-defined normalized and positive conditional distributions are natural by-products to our approach. The embedding is fast to compute and naturally accommodates learning problems ranging from prediction to classification. The theoretical findings are supplemented by favorable numerical results.

Samplets: A new paradigm for data compression

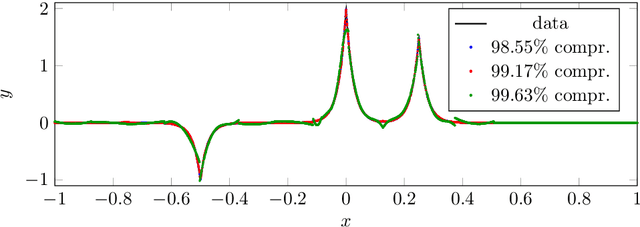
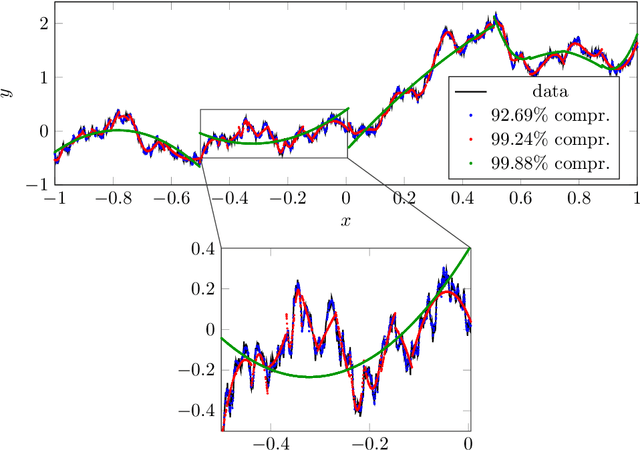
In this article, we introduce the concept of samplets by transferring the construction of Tausch-White wavelets to the realm of data. This way we obtain a multilevel representation of discrete data which directly enables data compression, detection of singularities and adaptivity. Applying samplets to represent kernel matrices, as they arise in kernel based learning or Gaussian process regression, we end up with quasi-sparse matrices. By thresholding small entries, these matrices are compressible to O(N log N) relevant entries, where N is the number of data points. This feature allows for the use of fill-in reducing reorderings to obtain a sparse factorization of the compressed matrices. Besides the comprehensive introduction to samplets and their properties, we present extensive numerical studies to benchmark the approach. Our results demonstrate that samplets mark a considerable step in the direction of making large data sets accessible for analysis.