Adaptive joint distribution learning

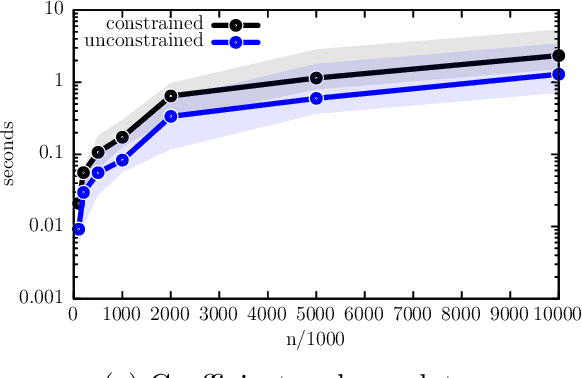
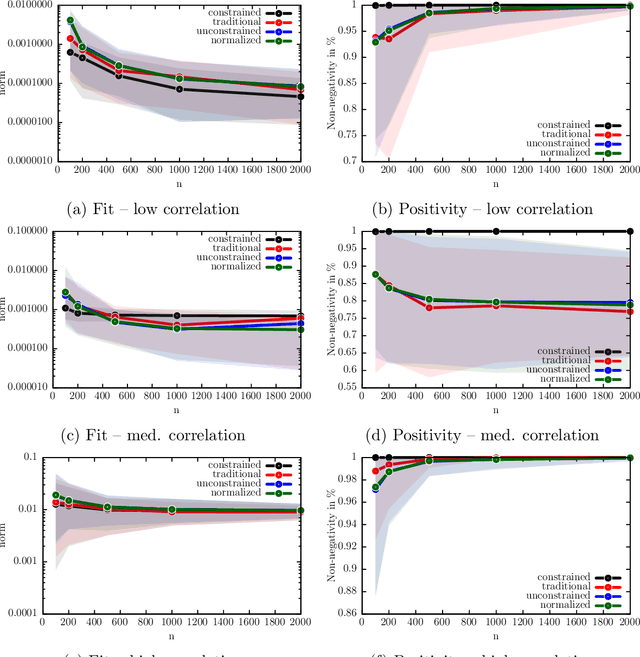
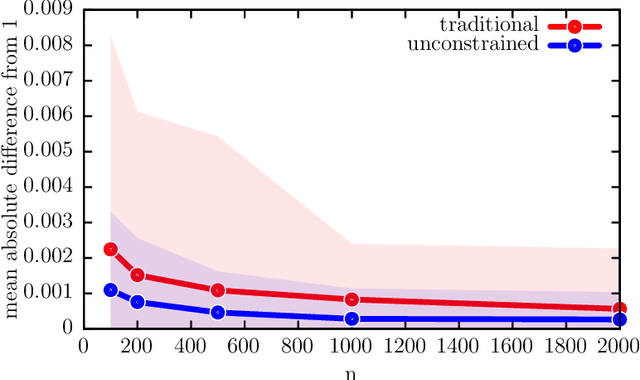
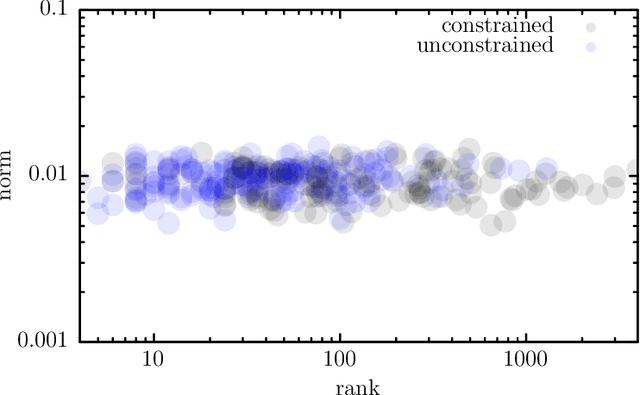
We develop a new framework for embedding (joint) probability distributions in tensor product reproducing kernel Hilbert spaces (RKHS). This framework accommodates a low-dimensional, positive, and normalized model of a Radon-Nikodym derivative, estimated from sample sizes of up to several million data points, alleviating the inherent limitations of RKHS modeling. Well-defined normalized and positive conditional distributions are natural by-products to our approach. The embedding is fast to compute and naturally accommodates learning problems ranging from prediction to classification. The theoretical findings are supplemented by favorable numerical results.