Joint Estimation of Conditional Mean and Covariance for Unbalanced Panels

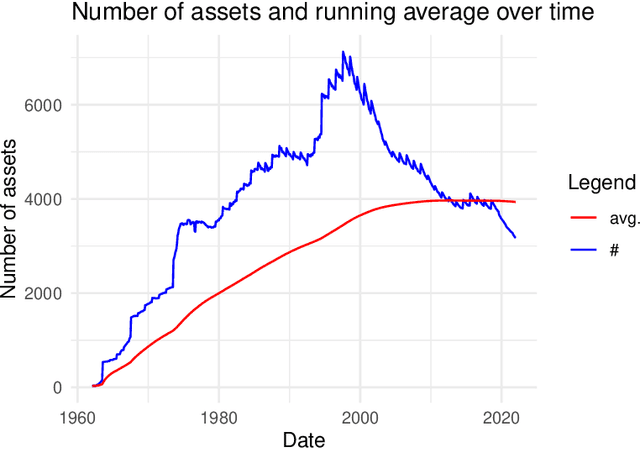
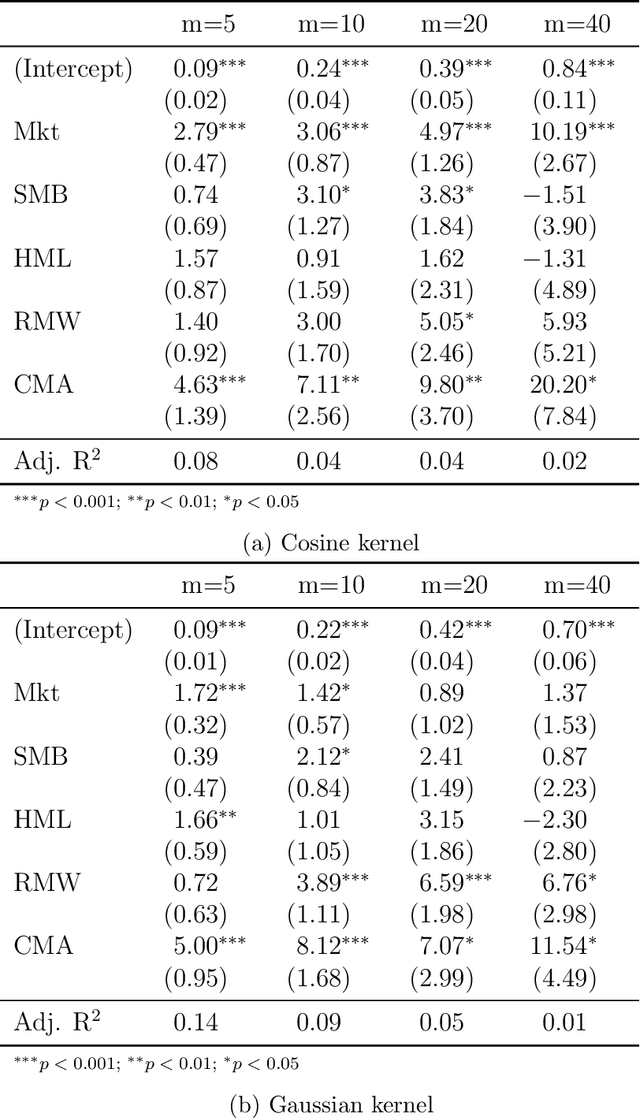
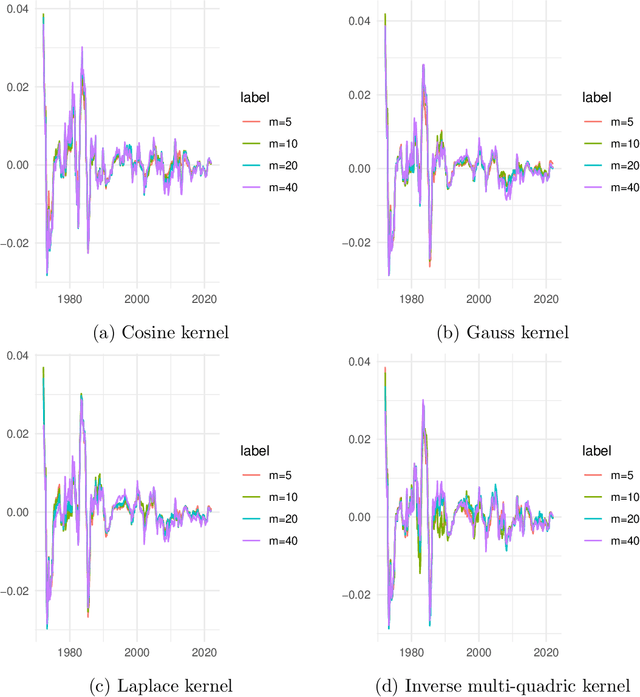
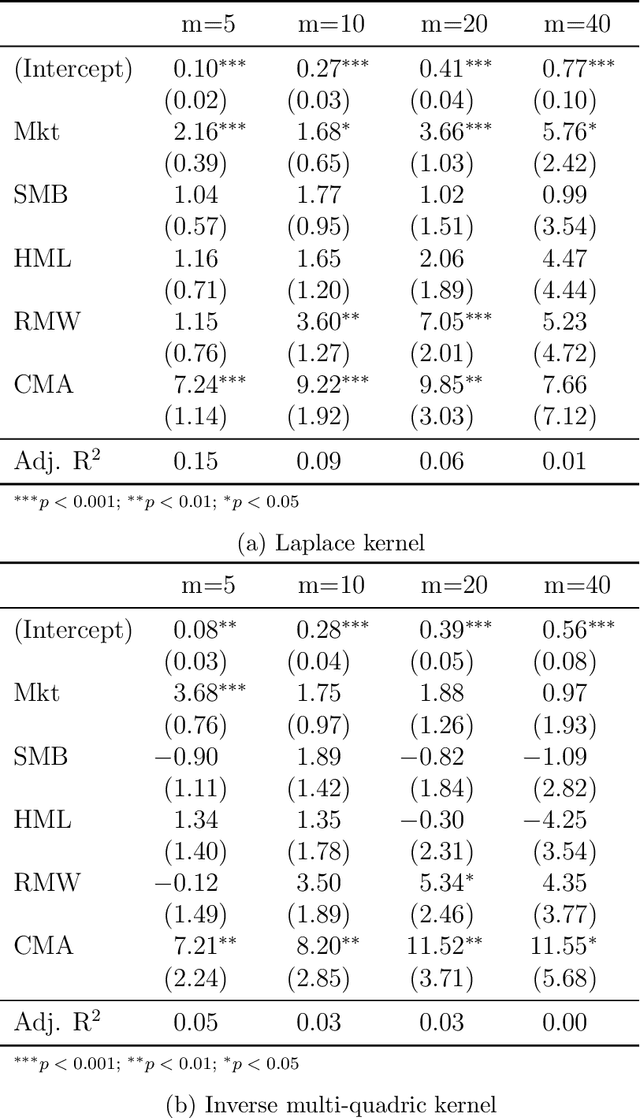
We propose a novel nonparametric kernel-based estimator of cross-sectional conditional mean and covariance matrices for large unbalanced panels. We show its consistency and provide finite-sample guarantees. In an empirical application, we estimate conditional mean and covariance matrices for a large unbalanced panel of monthly stock excess returns given macroeconomic and firm-specific covariates from 1962 to 2021.The estimator performs well with respect to statistical measures. It is informative for empirical asset pricing, generating conditional mean-variance efficient portfolios with substantial out-of-sample Sharpe ratios far beyond equal-weighted benchmarks.

Adaptive joint distribution learning

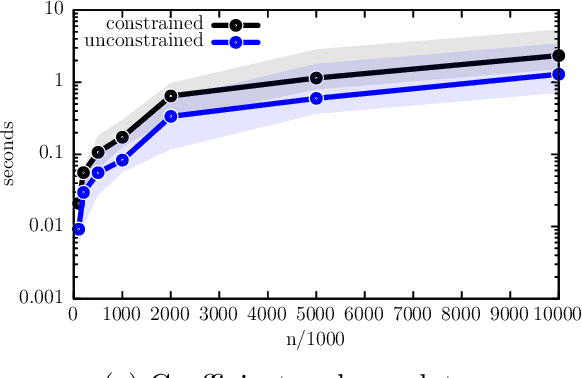
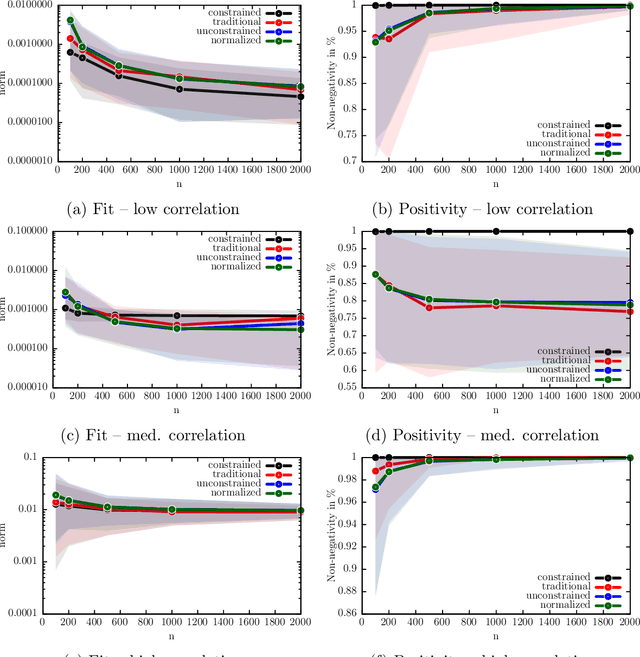
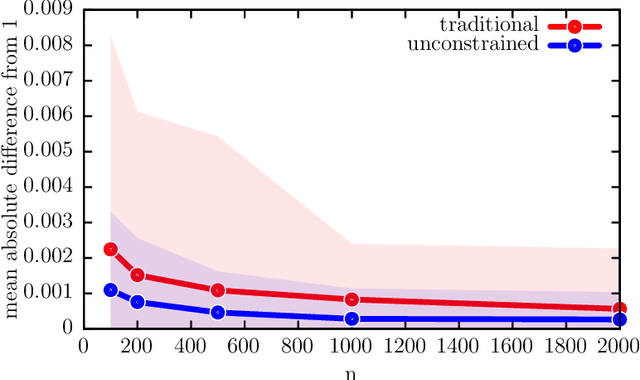
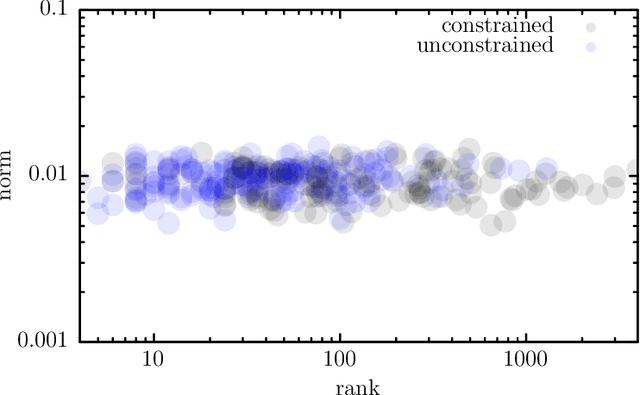
We develop a new framework for embedding (joint) probability distributions in tensor product reproducing kernel Hilbert spaces (RKHS). This framework accommodates a low-dimensional, positive, and normalized model of a Radon-Nikodym derivative, estimated from sample sizes of up to several million data points, alleviating the inherent limitations of RKHS modeling. Well-defined normalized and positive conditional distributions are natural by-products to our approach. The embedding is fast to compute and naturally accommodates learning problems ranging from prediction to classification. The theoretical findings are supplemented by favorable numerical results.