On Quasi-Localized Dual Pairs in Reproducing Kernel Hilbert Spaces

In scattered data approximation, the span of a finite number of translates of a chosen radial basis function is used as approximation space and the basis of translates is used for representing the approximate. However, this natural choice is by no means mandatory and different choices, like, for example, the Lagrange basis, are possible and might offer additional features. In this article, we discuss different alternatives together with their canonical duals. We study a localized version of the Lagrange basis, localized orthogonal bases, such as the Newton basis, and multiresolution versions thereof, constructed by means of samplets. We argue that the choice of orthogonal bases is particularly useful as they lead to symmetric preconditioners. All bases under consideration are compared numerically to illustrate their feasibility for scattered data approximation. We provide benchmark experiments in two spatial dimensions and consider the reconstruction of an implicit surface as a relevant application from computer graphics.

Samplet basis pursuit

We consider kernel-based learning in samplet coordinates with l1-regularization. The application of an l1-regularization term enforces sparsity of the coefficients with respect to the samplet basis. Therefore, we call this approach samplet basis pursuit. Samplets are wavelet-type signed measures, which are tailored to scattered data. They provide similar properties as wavelets in terms of localization, multiresolution analysis, and data compression. The class of signals that can sparsely be represented in a samplet basis is considerably larger than the class of signals which exhibit a sparse representation in the single-scale basis. In particular, every signal that can be represented by the superposition of only a few features of the canonical feature map is also sparse in samplet coordinates. We propose the efficient solution of the problem under consideration by combining soft-shrinkage with the semi-smooth Newton method and compare the approach to the fast iterative shrinkage thresholding algorithm. We present numerical benchmarks as well as applications to surface reconstruction from noisy data and to the reconstruction of temperature data using a dictionary of multiple kernels.

Samplets: A new paradigm for data compression

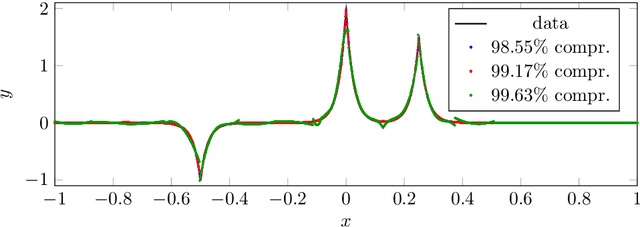
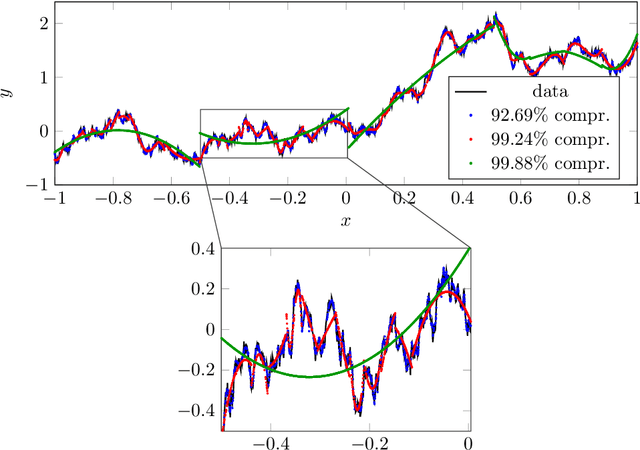
In this article, we introduce the concept of samplets by transferring the construction of Tausch-White wavelets to the realm of data. This way we obtain a multilevel representation of discrete data which directly enables data compression, detection of singularities and adaptivity. Applying samplets to represent kernel matrices, as they arise in kernel based learning or Gaussian process regression, we end up with quasi-sparse matrices. By thresholding small entries, these matrices are compressible to O(N log N) relevant entries, where N is the number of data points. This feature allows for the use of fill-in reducing reorderings to obtain a sparse factorization of the compressed matrices. Besides the comprehensive introduction to samplets and their properties, we present extensive numerical studies to benchmark the approach. Our results demonstrate that samplets mark a considerable step in the direction of making large data sets accessible for analysis.