Zdeněk Průša
Fast Matching Pursuit with Multi-Gabor Dictionaries
Feb 16, 2022
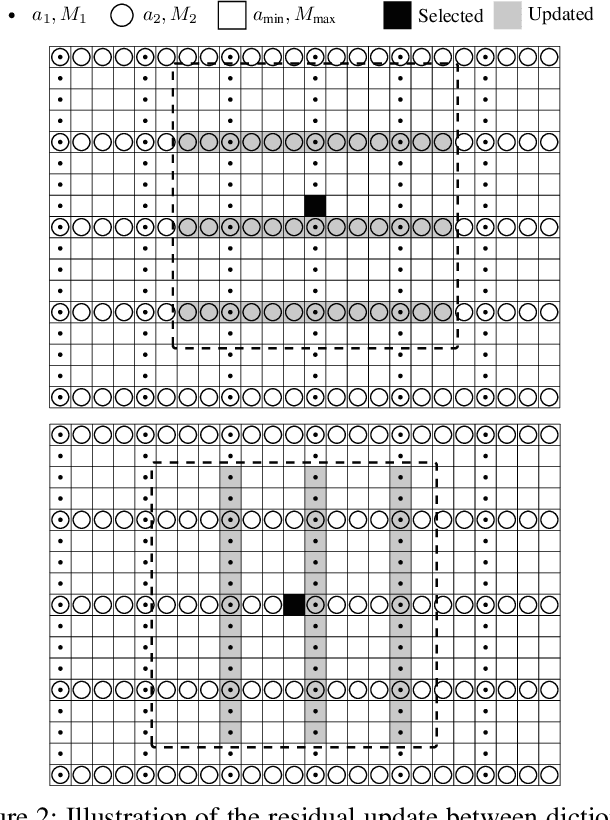


Abstract:Finding the best K-sparse approximation of a signal in a redundant dictionary is an NP-hard problem. Suboptimal greedy matching pursuit (MP) algorithms are generally used for this task. In this work, we present an acceleration technique and an implementation of the matching pursuit algorithm acting on a multi-Gabor dictionary, i.e., a concatenation of several Gabor-type time-frequency dictionaries, each of which consisting of translations and modulations of a possibly different window and time and frequency shift parameters. The technique is based on pre-computing and thresholding inner products between atoms and on updating the residual directly in the coefficient domain, i.e., without the round-trip to the signal domain. Since the proposed acceleration technique involves an approximate update step, we provide theoretical and experimental results illustrating the convergence of the resulting algorithm. The implementation is written in C (compatible with C99 and C++11) and we also provide Matlab and GNU Octave interfaces. For some settings, the implementation is up to 70 times faster than the standard Matching Pursuit Toolkit (MPTK).
Non-iterative Filter Bank Phase (Re)Construction
Feb 15, 2022



Abstract:Signal reconstruction from magnitude-only measurements presents a long-standing problem in signal processing. In this contribution, we propose a phase (re)construction method for filter banks with uniform decimation and controlled frequency variation. The suggested procedure extends the recently introduced phase-gradient heap integration and relies on a phase-magnitude relationship for filter bank coefficients obtained from Gaussian filters. Admissible filter banks are modeled as the discretization of certain generalized translation-invariant systems, for which we derive the phase-magnitude relationship explicitly. The implementation for discrete signals is described and the performance of the algorithm is evaluated on a range of real and synthetic signals.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge