High Resolution Seismic Waveform Generation using Denoising Diffusion

Accurate prediction and synthesis of seismic waveforms are crucial for seismic hazard assessment and earthquake-resistant infrastructure design. Existing prediction methods, such as Ground Motion Models and physics-based simulations, often fail to capture the full complexity of seismic wavefields, particularly at higher frequencies. This study introduces a novel, efficient, and scalable generative model for high-frequency seismic waveform generation. Our approach leverages a spectrogram representation of seismic waveform data, which is reduced to a lower-dimensional submanifold via an autoencoder. A state-of-the-art diffusion model is trained to generate this latent representation, conditioned on key input parameters: earthquake magnitude, recording distance, site conditions, and faulting type. The model generates waveforms with frequency content up to 50 Hz. Any scalar ground motion statistic, such as peak ground motion amplitudes and spectral accelerations, can be readily derived from the synthesized waveforms. We validate our model using commonly used seismological metrics, and performance metrics from image generation studies. Our results demonstrate that our openly available model can generate distributions of realistic high-frequency seismic waveforms across a wide range of input parameters, even in data-sparse regions. For the scalar ground motion statistics commonly used in seismic hazard and earthquake engineering studies, we show that the model accurately reproduces both the median trends of the real data and its variability. To evaluate and compare the growing number of this and similar 'Generative Waveform Models' (GWM), we argue that they should generally be openly available and that they should be included in community efforts for ground motion model evaluations.

Efficient algorithms for regularized Poisson Non-negative Matrix Factorization

We consider the problem of regularized Poisson Non-negative Matrix Factorization (NMF) problem, encompassing various regularization terms such as Lipschitz and relatively smooth functions, alongside linear constraints. This problem holds significant relevance in numerous Machine Learning applications, particularly within the domain of physical linear unmixing problems. A notable challenge arises from the main loss term in the Poisson NMF problem being a KL divergence, which is non-Lipschitz, rendering traditional gradient descent-based approaches inefficient. In this contribution, we explore the utilization of Block Successive Upper Minimization (BSUM) to overcome this challenge. We build approriate majorizing function for Lipschitz and relatively smooth functions, and show how to introduce linear constraints into the problem. This results in the development of two novel algorithms for regularized Poisson NMF. We conduct numerical simulations to showcase the effectiveness of our approach.

Efficient and Scalable Graph Generation through Iterative Local Expansion

In the realm of generative models for graphs, extensive research has been conducted. However, most existing methods struggle with large graphs due to the complexity of representing the entire joint distribution across all node pairs and capturing both global and local graph structures simultaneously. To overcome these issues, we introduce a method that generates a graph by progressively expanding a single node to a target graph. In each step, nodes and edges are added in a localized manner through denoising diffusion, building first the global structure, and then refining the local details. The local generation avoids modeling the entire joint distribution over all node pairs, achieving substantial computational savings with subquadratic runtime relative to node count while maintaining high expressivity through multiscale generation. Our experiments show that our model achieves state-of-the-art performance on well-established benchmark datasets while successfully scaling to graphs with at least 5000 nodes. Our method is also the first to successfully extrapolate to graphs outside of the training distribution, showcasing a much better generalization capability over existing methods.

An evaluation of deep learning models for predicting water depth evolution in urban floods

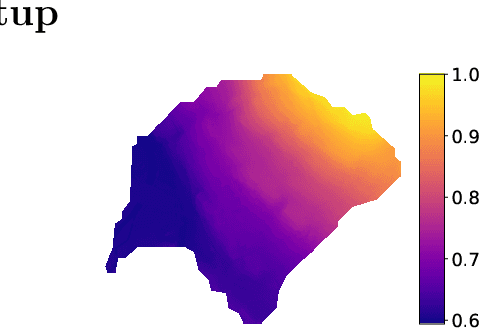
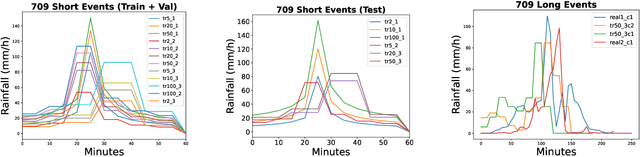
In this technical report we compare different deep learning models for prediction of water depth rasters at high spatial resolution. Efficient, accurate, and fast methods for water depth prediction are nowadays important as urban floods are increasing due to higher rainfall intensity caused by climate change, expansion of cities and changes in land use. While hydrodynamic models models can provide reliable forecasts by simulating water depth at every location of a catchment, they also have a high computational burden which jeopardizes their application to real-time prediction in large urban areas at high spatial resolution. Here, we propose to address this issue by using data-driven techniques. Specifically, we evaluate deep learning models which are trained to reproduce the data simulated by the CADDIES cellular-automata flood model, providing flood forecasts that can occur at different future time horizons. The advantage of using such models is that they can learn the underlying physical phenomena a priori, preventing manual parameter setting and computational burden. We perform experiments on a dataset consisting of two catchments areas within Switzerland with 18 simpler, short rainfall patterns and 4 long, more complex ones. Our results show that the deep learning models present in general lower errors compared to the other methods, especially for water depths $>0.5m$. However, when testing on more complex rainfall events or unseen catchment areas, the deep models do not show benefits over the simpler ones.

Diffusion Models for Graphs Benefit From Discrete State Spaces

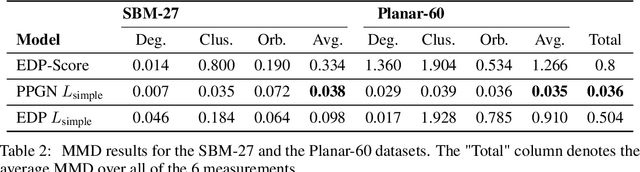
Denoising diffusion probabilistic models and score matching models have proven to be very powerful for generative tasks. While these approaches have also been applied to the generation of discrete graphs, they have, so far, relied on continuous Gaussian perturbations. Instead, in this work, we suggest using discrete noise for the forward Markov process. This ensures that in every intermediate step the graph remains discrete. Compared to the previous approach, our experimental results on four datasets and multiple architectures show that using a discrete noising process results in higher quality generated samples indicated with an average MMDs reduced by a factor of 1.5. Furthermore, the number of denoising steps is reduced from 1000 to 32 steps leading to a 30 times faster sampling procedure.

What You See is What You Classify: Black Box Attributions

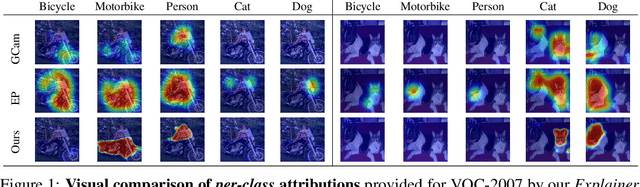
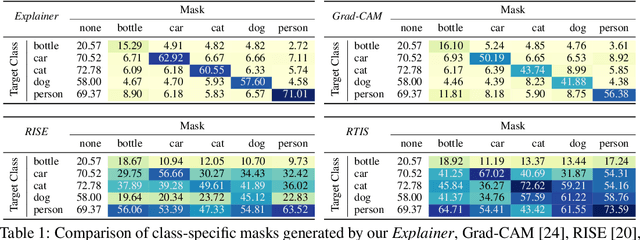
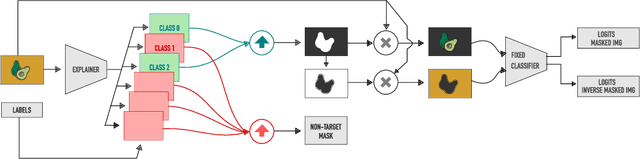
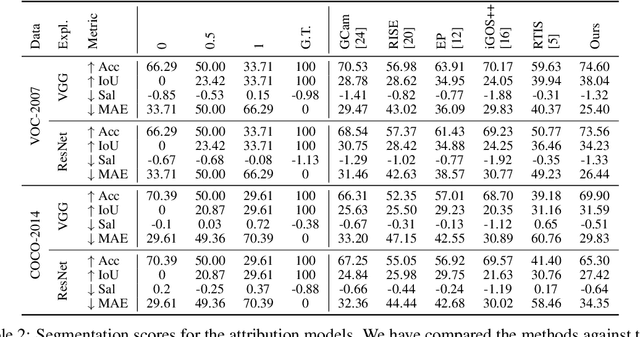
An important step towards explaining deep image classifiers lies in the identification of image regions that contribute to individual class scores in the model's output. However, doing this accurately is a difficult task due to the black-box nature of such networks. Most existing approaches find such attributions either using activations and gradients or by repeatedly perturbing the input. We instead address this challenge by training a second deep network, the Explainer, to predict attributions for a pre-trained black-box classifier, the Explanandum. These attributions are in the form of masks that only show the classifier-relevant parts of an image, masking out the rest. Our approach produces sharper and more boundary-precise masks when compared to the saliency maps generated by other methods. Moreover, unlike most existing approaches, ours is capable of directly generating very distinct class-specific masks. Finally, the proposed method is very efficient for inference since it only takes a single forward pass through the Explainer to generate all class-specific masks. We show that our attributions are superior to established methods both visually and quantitatively, by evaluating them on the PASCAL VOC-2007 and Microsoft COCO-2014 datasets.

SPECTRE : Spectral Conditioning Helps to Overcome the Expressivity Limits of One-shot Graph Generators

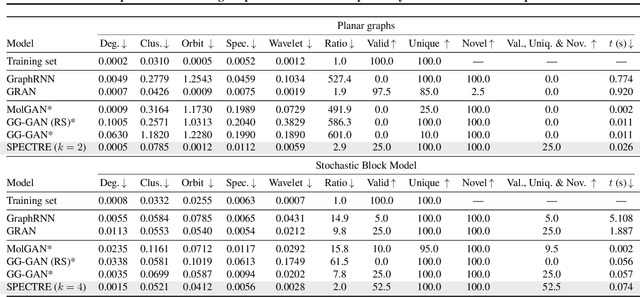
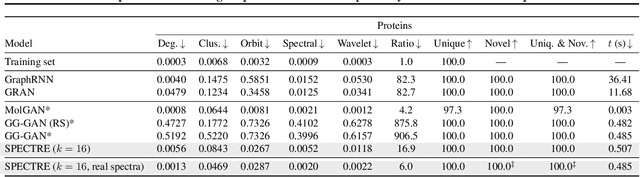
We approach the graph generation problem from a spectral perspective by first generating the dominant parts of the graph Laplacian spectrum and then building a graph matching these eigenvalues and eigenvectors. Spectral conditioning allows for direct modeling of the global and local graph structure and helps to overcome the expressivity and mode collapse issues of one-shot graph generators. Our novel GAN, called SPECTRE, enables the one-shot generation of much larger graphs than previously possible with one-shot models. SPECTRE outperforms state-of-the-art deep autoregressive generators in terms of modeling fidelity, while also avoiding expensive sequential generation and dependence on node ordering. A case in point, in sizable synthetic and real-world graphs SPECTRE achieves a 4-to-170 fold improvement over the best competitor that does not overfit and is 23-to-30 times faster than autoregressive generators.

A data acquisition setup for data driven acoustic design

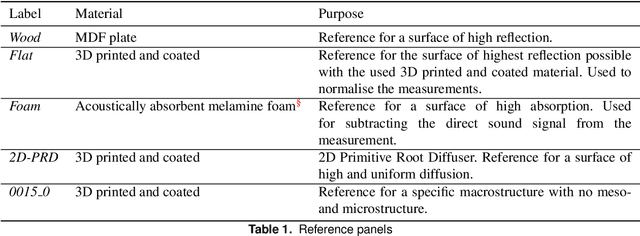
In this paper, we present a novel interdisciplinary approach to study the relationship between diffusive surface structures and their acoustic performance. Using computational design, surface structures are iteratively generated and 3D printed at 1:10 model scale. They originate from different fabrication typologies and are designed to have acoustic diffusion and absorption effects. An automated robotic process measures the impulse responses of these surfaces by positioning a microphone and a speaker at multiple locations. The collected data serves two purposes: first, as an exploratory catalogue of different spatio-temporal-acoustic scenarios and second, as data set for predicting the acoustic response of digitally designed surface geometries using machine learning. In this paper, we present the automated data acquisition setup, the data processing and the computational generation of diffusive surface structures. We describe first results of comparative studies of measured surface panels and conclude with steps of future research.

DeepSphere: a graph-based spherical CNN

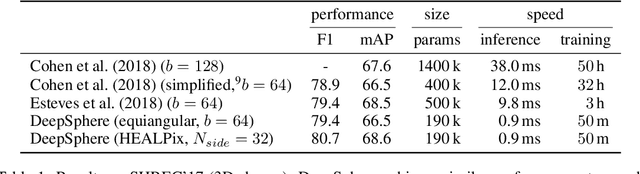
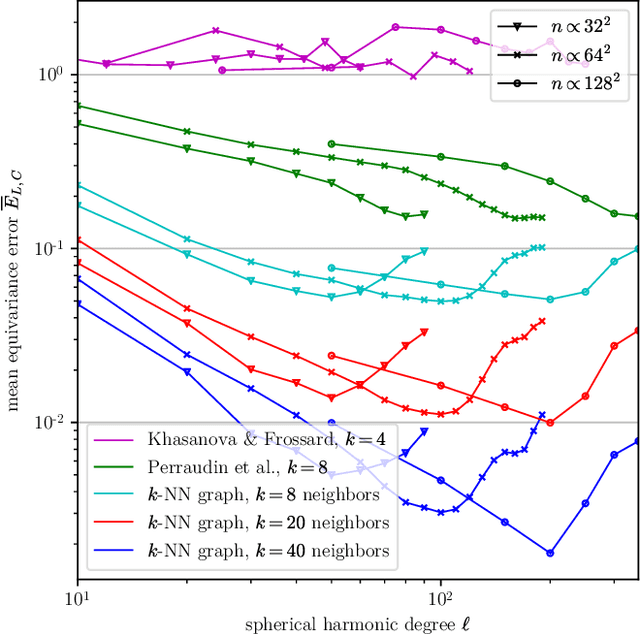
Designing a convolution for a spherical neural network requires a delicate tradeoff between efficiency and rotation equivariance. DeepSphere, a method based on a graph representation of the sampled sphere, strikes a controllable balance between these two desiderata. This contribution is twofold. First, we study both theoretically and empirically how equivariance is affected by the underlying graph with respect to the number of vertices and neighbors. Second, we evaluate DeepSphere on relevant problems. Experiments show state-of-the-art performance and demonstrates the efficiency and flexibility of this formulation. Perhaps surprisingly, comparison with previous work suggests that anisotropic filters might be an unnecessary price to pay. Our code is available at https://github.com/deepsphere

Scalable Graph Networks for Particle Simulations

Learning system dynamics directly from observations is a promising direction in machine learning due to its potential to significantly enhance our ability to understand physical systems. However, the dynamics of many real-world systems are challenging to learn due to the presence of nonlinear potentials and a number of interactions that scales quadratically with the number of particles $N$, as in the case of the N-body problem. In this work, we introduce an approach that transforms a fully-connected interaction graph into a hierarchical one which reduces the number of edges to $O(N)$. This results in linear time and space complexity while the pre-computation of the hierarchical graph requires $O(N\log (N))$ time and $O(N)$ space. Using our approach, we are able to train models on much larger particle counts, even on a single GPU. We evaluate how the phase space position accuracy and energy conservation depend on the number of simulated particles. Our approach retains high accuracy and efficiency even on large-scale gravitational N-body simulations which are impossible to run on a single machine if a fully-connected graph is used. Similar results are also observed when simulating Coulomb interactions. Furthermore, we make several important observations regarding the performance of this new hierarchical model, including: i) its accuracy tends to improve with the number of particles in the simulation and ii) its generalisation to unseen particle counts is also much better than for models that use all $O(N^2)$ interactions.