Generalizing to any diverse distribution: uniformity, gentle finetuning and rebalancing

As training datasets grow larger, we aspire to develop models that generalize well to any diverse test distribution, even if the latter deviates significantly from the training data. Various approaches like domain adaptation, domain generalization, and robust optimization attempt to address the out-of-distribution challenge by posing assumptions about the relation between training and test distribution. Differently, we adopt a more conservative perspective by accounting for the worst-case error across all sufficiently diverse test distributions within a known domain. Our first finding is that training on a uniform distribution over this domain is optimal. We also interrogate practical remedies when uniform samples are unavailable by considering methods for mitigating non-uniformity through finetuning and rebalancing. Our theory provides a mathematical grounding for previous observations on the role of entropy and rebalancing for o.o.d. generalization and foundation model training. We also provide new empirical evidence across tasks involving o.o.d. shifts which illustrate the broad applicability of our perspective.

Efficient and Scalable Graph Generation through Iterative Local Expansion

In the realm of generative models for graphs, extensive research has been conducted. However, most existing methods struggle with large graphs due to the complexity of representing the entire joint distribution across all node pairs and capturing both global and local graph structures simultaneously. To overcome these issues, we introduce a method that generates a graph by progressively expanding a single node to a target graph. In each step, nodes and edges are added in a localized manner through denoising diffusion, building first the global structure, and then refining the local details. The local generation avoids modeling the entire joint distribution over all node pairs, achieving substantial computational savings with subquadratic runtime relative to node count while maintaining high expressivity through multiscale generation. Our experiments show that our model achieves state-of-the-art performance on well-established benchmark datasets while successfully scaling to graphs with at least 5000 nodes. Our method is also the first to successfully extrapolate to graphs outside of the training distribution, showcasing a much better generalization capability over existing methods.

AbDiffuser: Full-Atom Generation of In-Vitro Functioning Antibodies

We introduce AbDiffuser, an equivariant and physics-informed diffusion model for the joint generation of antibody 3D structures and sequences. AbDiffuser is built on top of a new representation of protein structure, relies on a novel architecture for aligned proteins, and utilizes strong diffusion priors to improve the denoising process. Our approach improves protein diffusion by taking advantage of domain knowledge and physics-based constraints; handles sequence-length changes; and reduces memory complexity by an order of magnitude enabling backbone and side chain generation. We validate AbDiffuser in silico and in vitro. Numerical experiments showcase the ability of AbDiffuser to generate antibodies that closely track the sequence and structural properties of a reference set. Laboratory experiments confirm that all 16 HER2 antibodies discovered were expressed at high levels and that 57.1% of selected designs were tight binders.

Discovering Graph Generation Algorithms

We provide a novel approach to construct generative models for graphs. Instead of using the traditional probabilistic models or deep generative models, we propose to instead find an algorithm that generates the data. We achieve this using evolutionary search and a powerful fitness function, implemented by a randomly initialized graph neural network. This brings certain advantages over current deep generative models, for instance, a higher potential for out-of-training-distribution generalization and direct interpretability, as the final graph generative process is expressed as a Python function. We show that this approach can be competitive with deep generative models and under some circumstances can even find the true graph generative process, and as such perfectly generalize.

Automating Rigid Origami Design

While rigid origami has shown potential in a large diversity of engineering applications, current rigid origami crease pattern designs mostly rely on known tessellations. This leaves a potential gap in performance as the space of rigidly foldable crease patterns is far larger than these tessellations would suggest. In this work, we build upon the recently developed principle of three units method to formulate rigid origami design as a discrete optimization problem. Our implementation allows for a simple definition of diverse objectives and thereby expands the potential of rigid origami further to optimized, application-specific crease patterns. We benchmark a diverse set of search methods in several shape approximation tasks to validate our model and showcase the flexibility of our formulation through four illustrative case studies. Results show that using our proposed problem formulation one can successfully approximate a variety of target shapes. Moreover, by specifying custom reward functions, we can find patterns, which result in novel, foldable designs for everyday objects.

Diffusion Models for Graphs Benefit From Discrete State Spaces

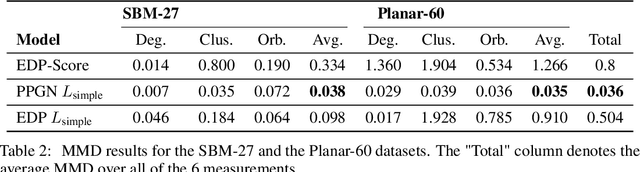
Denoising diffusion probabilistic models and score matching models have proven to be very powerful for generative tasks. While these approaches have also been applied to the generation of discrete graphs, they have, so far, relied on continuous Gaussian perturbations. Instead, in this work, we suggest using discrete noise for the forward Markov process. This ensures that in every intermediate step the graph remains discrete. Compared to the previous approach, our experimental results on four datasets and multiple architectures show that using a discrete noising process results in higher quality generated samples indicated with an average MMDs reduced by a factor of 1.5. Furthermore, the number of denoising steps is reduced from 1000 to 32 steps leading to a 30 times faster sampling procedure.

Agent-based Graph Neural Networks

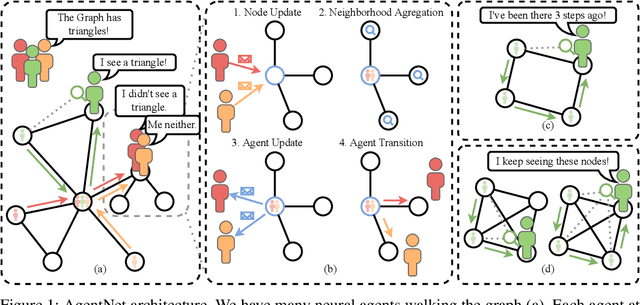
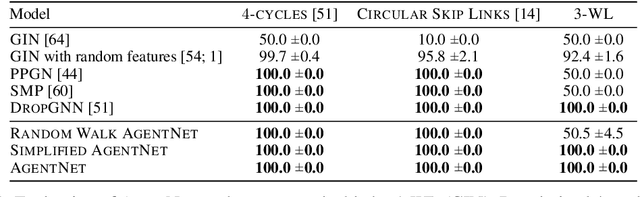
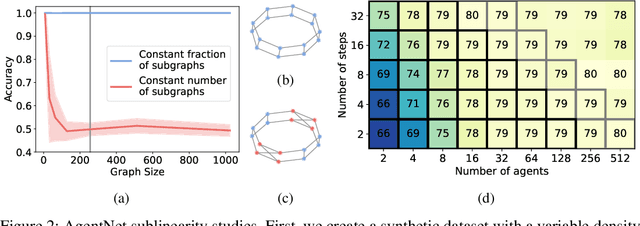
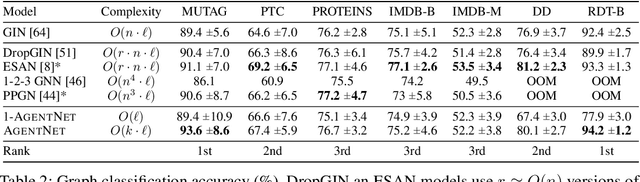
We present a novel graph neural network we call AgentNet, which is designed specifically for graph-level tasks. AgentNet is inspired by sublinear algorithms, featuring a computational complexity that is independent of the graph size. The architecture of AgentNet differs fundamentally from the architectures of known graph neural networks. In AgentNet, some trained \textit{neural agents} intelligently walk the graph, and then collectively decide on the output. We provide an extensive theoretical analysis of AgentNet: We show that the agents can learn to systematically explore their neighborhood and that AgentNet can distinguish some structures that are even indistinguishable by 3-WL. Moreover, AgentNet is able to separate any two graphs which are sufficiently different in terms of subgraphs. We confirm these theoretical results with synthetic experiments on hard-to-distinguish graphs and real-world graph classification tasks. In both cases, we compare favorably not only to standard GNNs but also to computationally more expensive GNN extensions.

DT+GNN: A Fully Explainable Graph Neural Network using Decision Trees

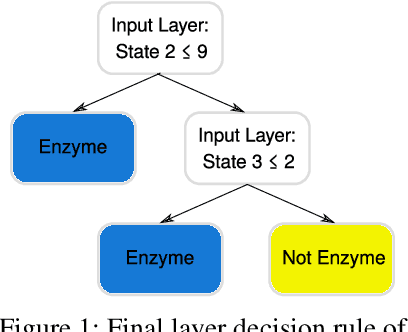
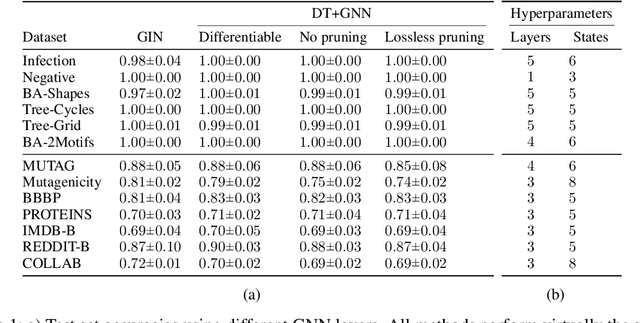
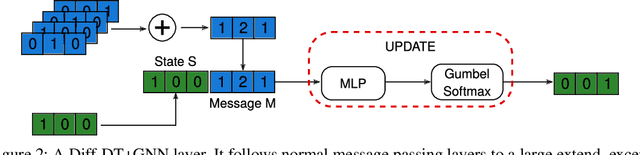
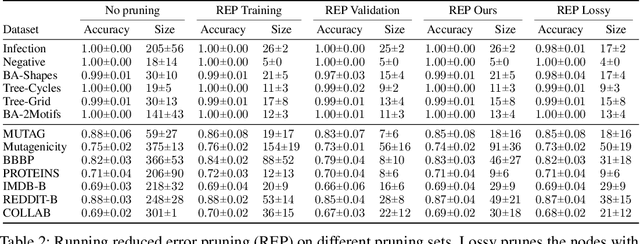
We propose the fully explainable Decision Tree Graph Neural Network (DT+GNN) architecture. In contrast to existing black-box GNNs and post-hoc explanation methods, the reasoning of DT+GNN can be inspected at every step. To achieve this, we first construct a differentiable GNN layer, which uses a categorical state space for nodes and messages. This allows us to convert the trained MLPs in the GNN into decision trees. These trees are pruned using our newly proposed method to ensure they are small and easy to interpret. We can also use the decision trees to compute traditional explanations. We demonstrate on both real-world datasets and synthetic GNN explainability benchmarks that this architecture works as well as traditional GNNs. Furthermore, we leverage the explainability of DT+GNNs to find interesting insights into many of these datasets, with some surprising results. We also provide an interactive web tool to inspect DT+GNN's decision making.

SPECTRE : Spectral Conditioning Helps to Overcome the Expressivity Limits of One-shot Graph Generators

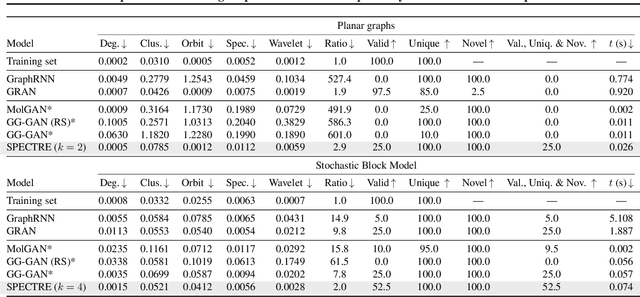
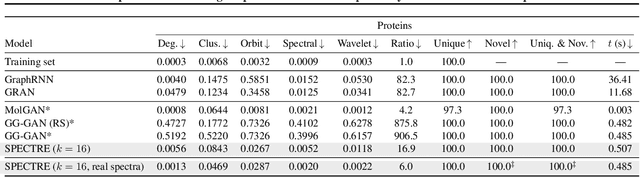
We approach the graph generation problem from a spectral perspective by first generating the dominant parts of the graph Laplacian spectrum and then building a graph matching these eigenvalues and eigenvectors. Spectral conditioning allows for direct modeling of the global and local graph structure and helps to overcome the expressivity and mode collapse issues of one-shot graph generators. Our novel GAN, called SPECTRE, enables the one-shot generation of much larger graphs than previously possible with one-shot models. SPECTRE outperforms state-of-the-art deep autoregressive generators in terms of modeling fidelity, while also avoiding expensive sequential generation and dependence on node ordering. A case in point, in sizable synthetic and real-world graphs SPECTRE achieves a 4-to-170 fold improvement over the best competitor that does not overfit and is 23-to-30 times faster than autoregressive generators.

DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks

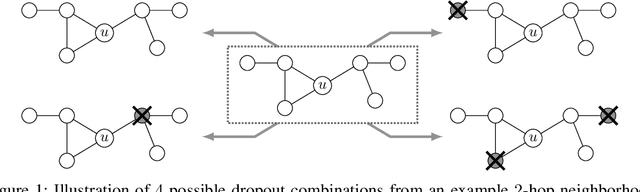
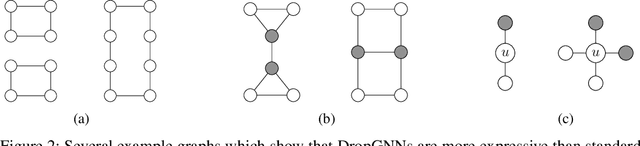
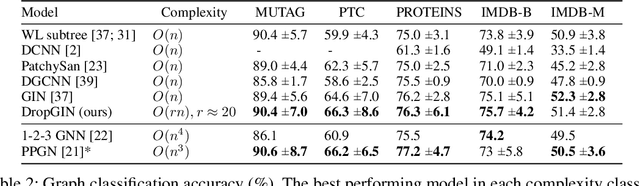
This paper studies Dropout Graph Neural Networks (DropGNNs), a new approach that aims to overcome the limitations of standard GNN frameworks. In DropGNNs, we execute multiple runs of a GNN on the input graph, with some of the nodes randomly and independently dropped in each of these runs. Then, we combine the results of these runs to obtain the final result. We prove that DropGNNs can distinguish various graph neighborhoods that cannot be separated by message passing GNNs. We derive theoretical bounds for the number of runs required to ensure a reliable distribution of dropouts, and we prove several properties regarding the expressive capabilities and limits of DropGNNs. We experimentally validate our theoretical findings on expressiveness. Furthermore, we show that DropGNNs perform competitively on established GNN benchmarks.