Agent-based Graph Neural Networks
Paper and Code
Jun 22, 2022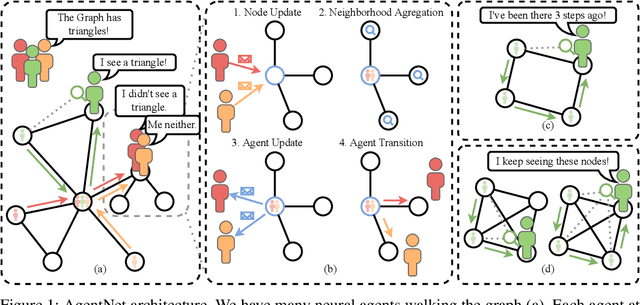
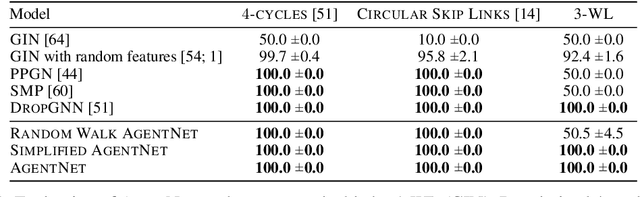
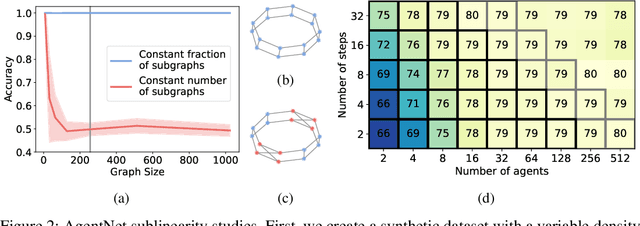
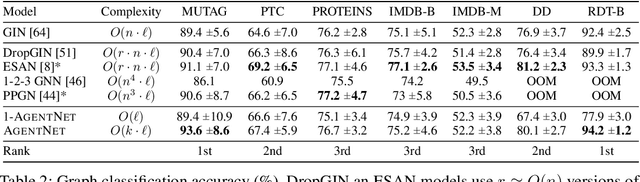
We present a novel graph neural network we call AgentNet, which is designed specifically for graph-level tasks. AgentNet is inspired by sublinear algorithms, featuring a computational complexity that is independent of the graph size. The architecture of AgentNet differs fundamentally from the architectures of known graph neural networks. In AgentNet, some trained \textit{neural agents} intelligently walk the graph, and then collectively decide on the output. We provide an extensive theoretical analysis of AgentNet: We show that the agents can learn to systematically explore their neighborhood and that AgentNet can distinguish some structures that are even indistinguishable by 3-WL. Moreover, AgentNet is able to separate any two graphs which are sufficiently different in terms of subgraphs. We confirm these theoretical results with synthetic experiments on hard-to-distinguish graphs and real-world graph classification tasks. In both cases, we compare favorably not only to standard GNNs but also to computationally more expensive GNN extensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge