Agent-based Graph Neural Networks

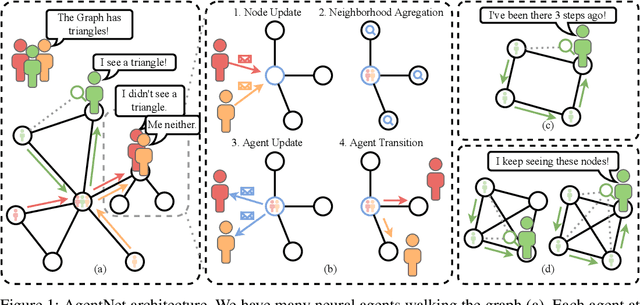
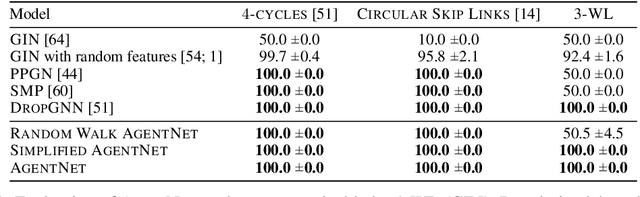
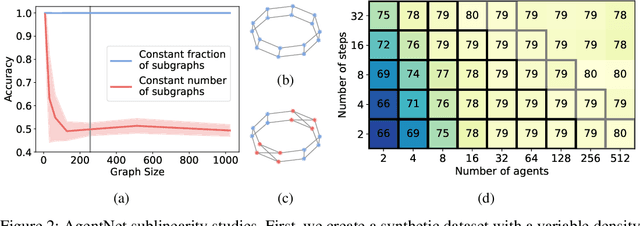
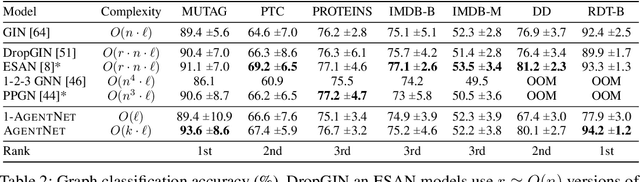
We present a novel graph neural network we call AgentNet, which is designed specifically for graph-level tasks. AgentNet is inspired by sublinear algorithms, featuring a computational complexity that is independent of the graph size. The architecture of AgentNet differs fundamentally from the architectures of known graph neural networks. In AgentNet, some trained \textit{neural agents} intelligently walk the graph, and then collectively decide on the output. We provide an extensive theoretical analysis of AgentNet: We show that the agents can learn to systematically explore their neighborhood and that AgentNet can distinguish some structures that are even indistinguishable by 3-WL. Moreover, AgentNet is able to separate any two graphs which are sufficiently different in terms of subgraphs. We confirm these theoretical results with synthetic experiments on hard-to-distinguish graphs and real-world graph classification tasks. In both cases, we compare favorably not only to standard GNNs but also to computationally more expensive GNN extensions.

A Theoretical Comparison of Graph Neural Network Extensions

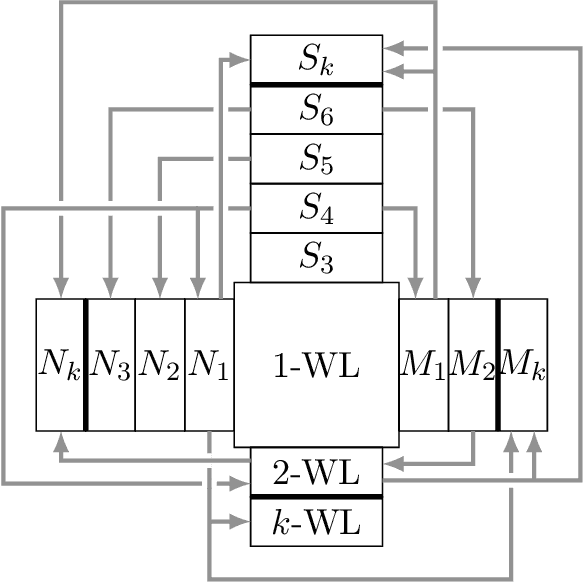
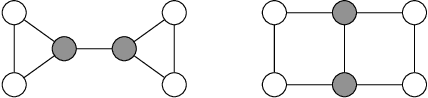
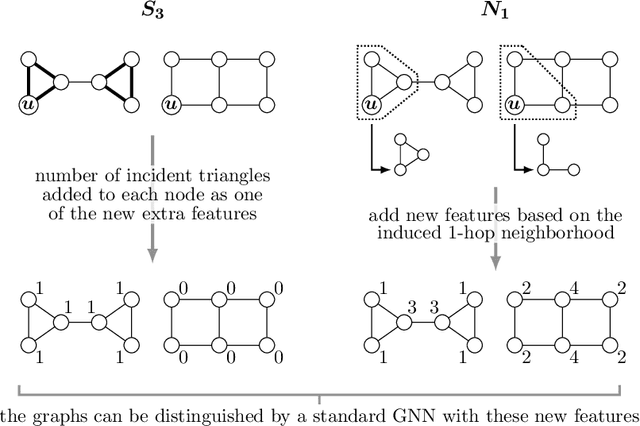
We study and compare different Graph Neural Network extensions that increase the expressive power of GNNs beyond the Weisfeiler-Leman test. We focus on (i) GNNs based on higher order WL methods, (ii) GNNs that preprocess small substructures in the graph, (iii) GNNs that preprocess the graph up to a small radius, and (iv) GNNs that slightly perturb the graph to compute an embedding. We begin by presenting a simple improvement for this last extension that strictly increases the expressive power of this GNN variant. Then, as our main result, we compare the expressiveness of these extensions to each other through a series of example constructions that can be distinguished by one of the extensions, but not by another one. We also show negative examples that are particularly challenging for each of the extensions, and we prove several claims about the ability of these extensions to count cliques and cycles in the graph.

DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks

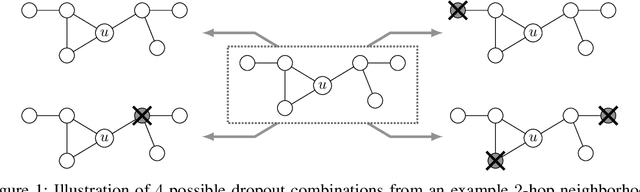
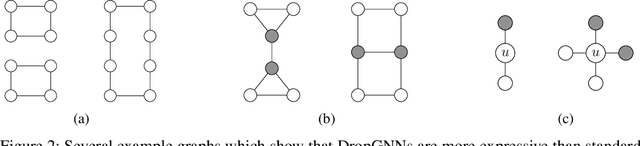
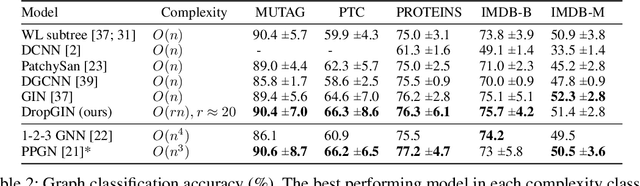
This paper studies Dropout Graph Neural Networks (DropGNNs), a new approach that aims to overcome the limitations of standard GNN frameworks. In DropGNNs, we execute multiple runs of a GNN on the input graph, with some of the nodes randomly and independently dropped in each of these runs. Then, we combine the results of these runs to obtain the final result. We prove that DropGNNs can distinguish various graph neighborhoods that cannot be separated by message passing GNNs. We derive theoretical bounds for the number of runs required to ensure a reliable distribution of dropouts, and we prove several properties regarding the expressive capabilities and limits of DropGNNs. We experimentally validate our theoretical findings on expressiveness. Furthermore, we show that DropGNNs perform competitively on established GNN benchmarks.