A Theoretical Comparison of Graph Neural Network Extensions
Paper and Code
Jan 30, 2022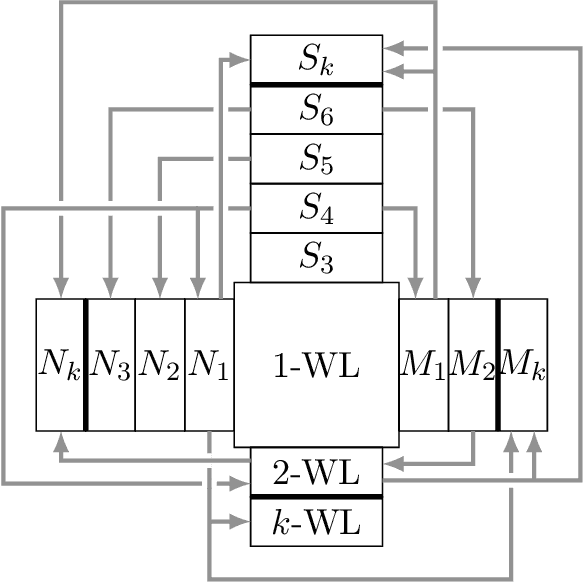
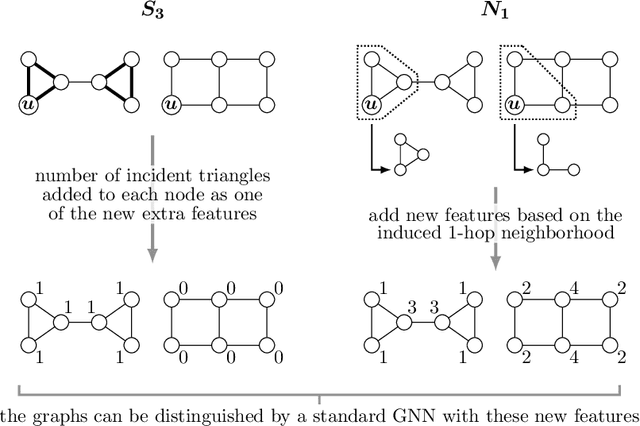

We study and compare different Graph Neural Network extensions that increase the expressive power of GNNs beyond the Weisfeiler-Leman test. We focus on (i) GNNs based on higher order WL methods, (ii) GNNs that preprocess small substructures in the graph, (iii) GNNs that preprocess the graph up to a small radius, and (iv) GNNs that slightly perturb the graph to compute an embedding. We begin by presenting a simple improvement for this last extension that strictly increases the expressive power of this GNN variant. Then, as our main result, we compare the expressiveness of these extensions to each other through a series of example constructions that can be distinguished by one of the extensions, but not by another one. We also show negative examples that are particularly challenging for each of the extensions, and we prove several claims about the ability of these extensions to count cliques and cycles in the graph.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge