DT+GNN: A Fully Explainable Graph Neural Network using Decision Trees

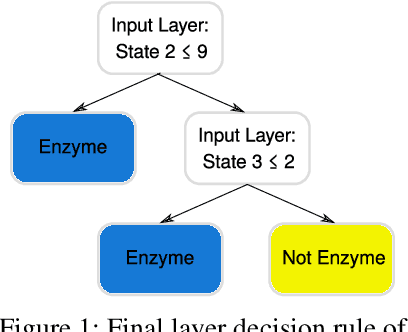
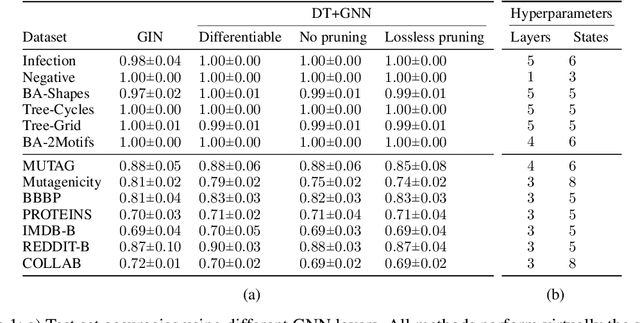
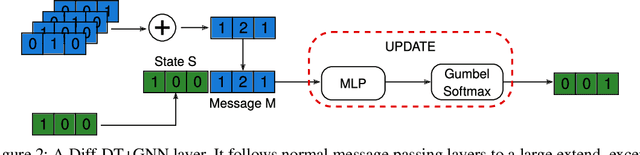
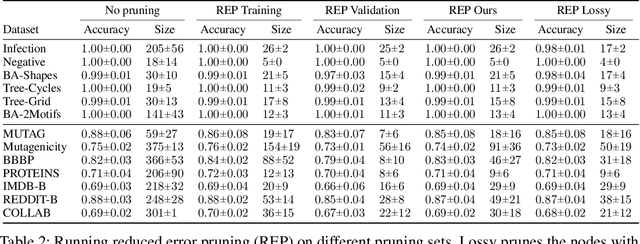
We propose the fully explainable Decision Tree Graph Neural Network (DT+GNN) architecture. In contrast to existing black-box GNNs and post-hoc explanation methods, the reasoning of DT+GNN can be inspected at every step. To achieve this, we first construct a differentiable GNN layer, which uses a categorical state space for nodes and messages. This allows us to convert the trained MLPs in the GNN into decision trees. These trees are pruned using our newly proposed method to ensure they are small and easy to interpret. We can also use the decision trees to compute traditional explanations. We demonstrate on both real-world datasets and synthetic GNN explainability benchmarks that this architecture works as well as traditional GNNs. Furthermore, we leverage the explainability of DT+GNNs to find interesting insights into many of these datasets, with some surprising results. We also provide an interactive web tool to inspect DT+GNN's decision making.

Asynchronous Neural Networks for Learning in Graphs

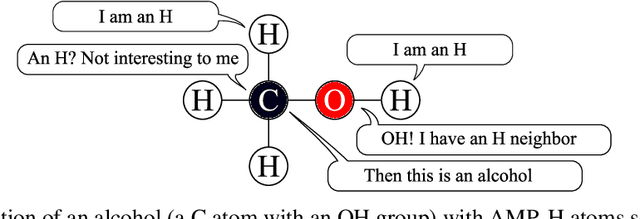
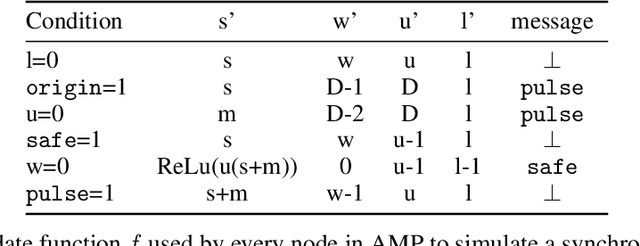
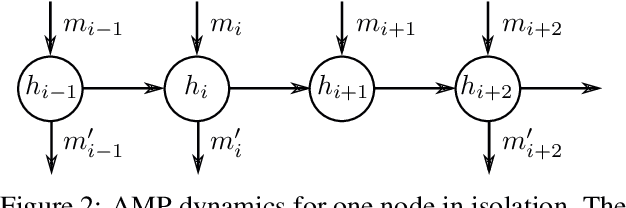
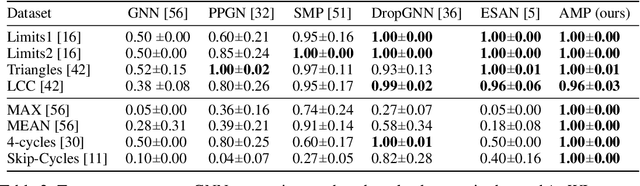
This paper studies asynchronous message passing (AMP), a new paradigm for applying neural network based learning to graphs. Existing graph neural networks use the synchronous distributed computing model and aggregate their neighbors in each round, which causes problems such as oversmoothing and limits their expressiveness. On the other hand, AMP is based on the asynchronous model, where nodes react to messages of their neighbors individually. We prove that (i) AMP can simulate synchronous GNNs and that (ii) AMP can theoretically distinguish any pair of graphs. We experimentally validate AMP's expressiveness. Further, we show that AMP might be better suited to propagate messages over large distances in graphs and performs well on several graph classification benchmarks.

DropGNN: Random Dropouts Increase the Expressiveness of Graph Neural Networks

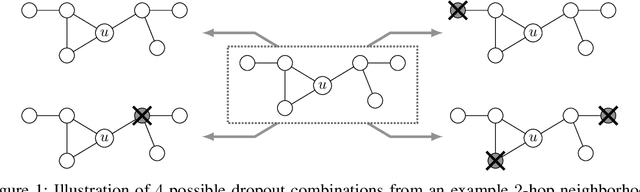
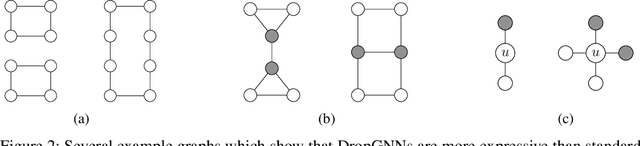
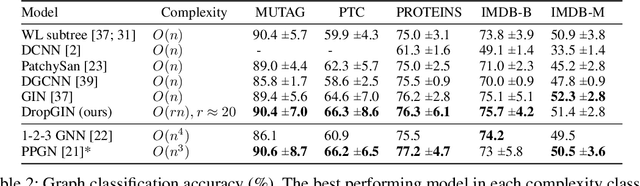
This paper studies Dropout Graph Neural Networks (DropGNNs), a new approach that aims to overcome the limitations of standard GNN frameworks. In DropGNNs, we execute multiple runs of a GNN on the input graph, with some of the nodes randomly and independently dropped in each of these runs. Then, we combine the results of these runs to obtain the final result. We prove that DropGNNs can distinguish various graph neighborhoods that cannot be separated by message passing GNNs. We derive theoretical bounds for the number of runs required to ensure a reliable distribution of dropouts, and we prove several properties regarding the expressive capabilities and limits of DropGNNs. We experimentally validate our theoretical findings on expressiveness. Furthermore, we show that DropGNNs perform competitively on established GNN benchmarks.

Should Graph Neural Networks Use Features, Edges, Or Both?

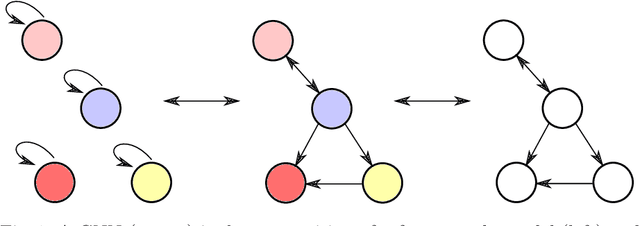
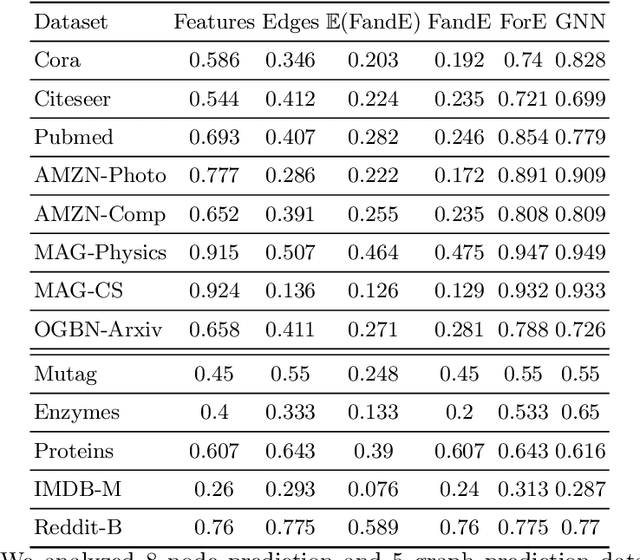
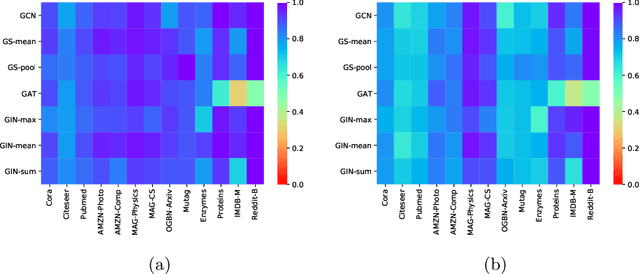
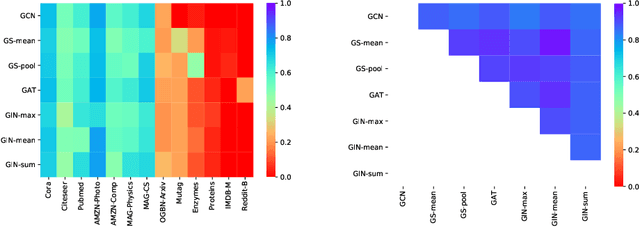
Graph Neural Networks (GNNs) are the first choice for learning algorithms on graph data. GNNs promise to integrate (i) node features as well as (ii) edge information in an end-to-end learning algorithm. How does this promise work out practically? In this paper, we study to what extend GNNs are necessary to solve prominent graph classification problems. We find that for graph classification, a GNN is not more than the sum of its parts. We also find that, unlike features, predictions with an edge-only model do not always transfer to GNNs.

Towards Robust Graph Contrastive Learning

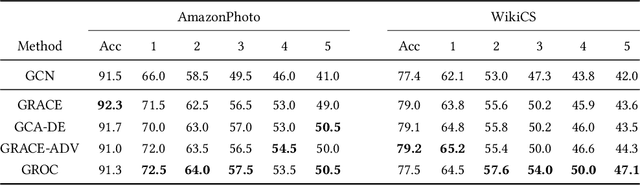
We study the problem of adversarially robust self-supervised learning on graphs. In the contrastive learning framework, we introduce a new method that increases the adversarial robustness of the learned representations through i) adversarial transformations and ii) transformations that not only remove but also insert edges. We evaluate the learned representations in a preliminary set of experiments, obtaining promising results. We believe this work takes an important step towards incorporating robustness as a viable auxiliary task in graph contrastive learning.

Contrastive Graph Neural Network Explanation

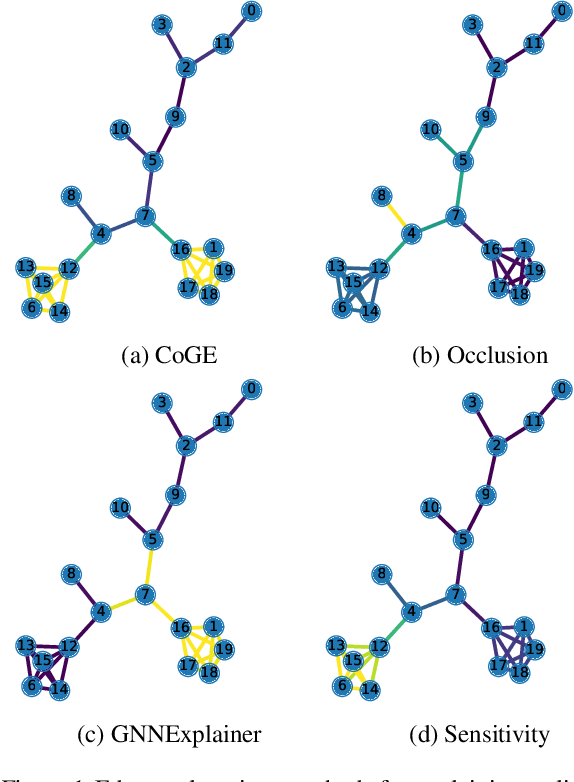
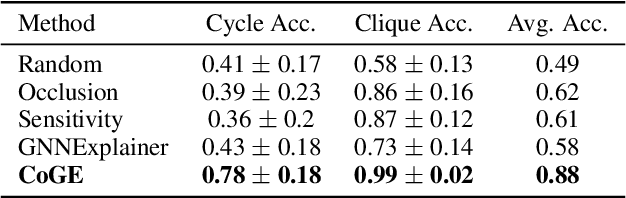
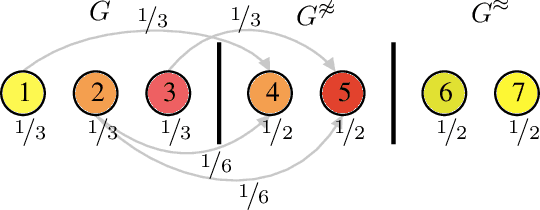
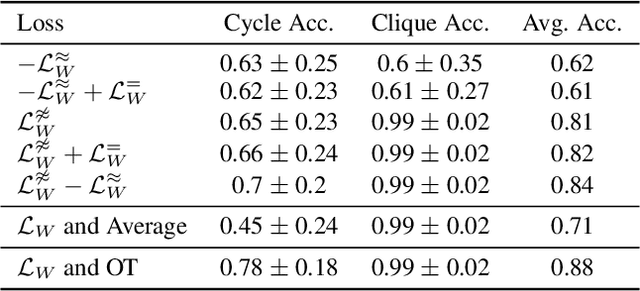
Graph Neural Networks achieve remarkable results on problems with structured data but come as black-box predictors. Transferring existing explanation techniques, such as occlusion, fails as even removing a single node or edge can lead to drastic changes in the graph. The resulting graphs can differ from all training examples, causing model confusion and wrong explanations. Thus, we argue that explicability must use graphs compliant with the distribution underlying the training data. We coin this property Distribution Compliant Explanation (DCE) and present a novel Contrastive GNN Explanation (CoGE) technique following this paradigm. An experimental study supports the efficacy of CoGE.

Medley2K: A Dataset of Medley Transitions

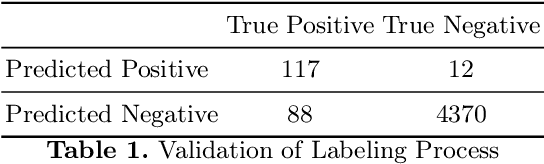
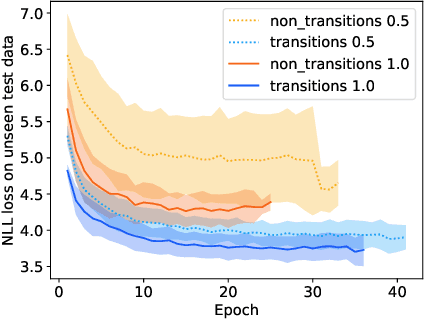
The automatic generation of medleys, i.e., musical pieces formed by different songs concatenated via smooth transitions, is not well studied in the current literature. To facilitate research on this topic, we make available a dataset called Medley2K that consists of 2,000 medleys and 7,712 labeled transitions. Our dataset features a rich variety of song transitions across different music genres. We provide a detailed description of this dataset and validate it by training a state-of-the-art generative model in the task of generating transitions between songs.

Neural Status Registers

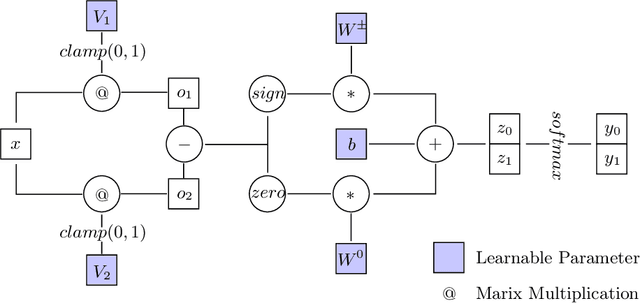
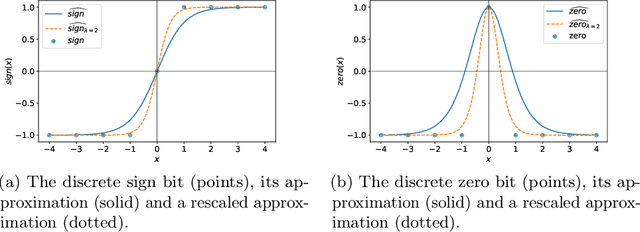
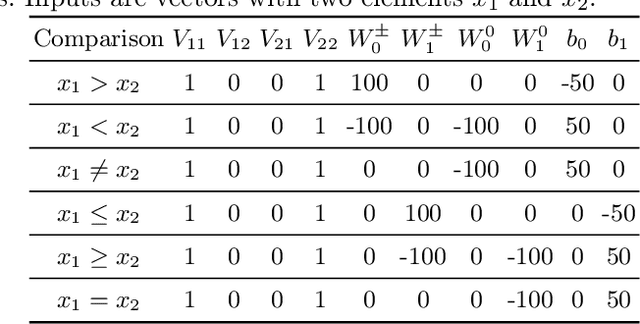
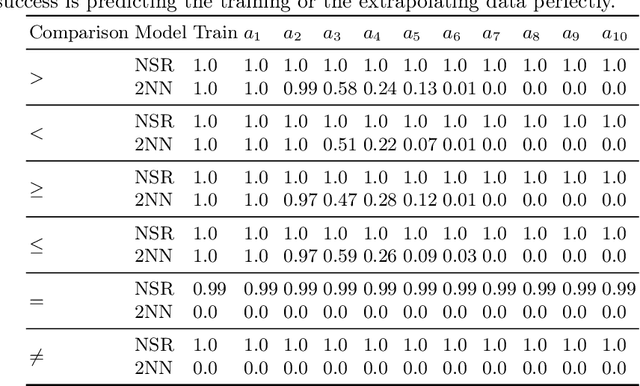
Neural networks excel at approximating functions and finding patterns in complex and challenging domains. Yet, they fail to learn simple but precise computation. Recent work addressed the ability to add, subtract, and multiply numbers but is lacking a component to drive control flow. True computer intelligence should also be able to decide when to perform what operation. In this paper, we introduce the Neural Status Register (NSR), inspired by physical Status Registers. At the heart of the NSR are arithmetic comparisons between inputs. With theoretically principled changes to physical Status Registers, the NSR allows end-to-end differentiation and learns such comparisons reliably. But the NSR also extrapolates: it generalizes to unseen data distributions. For example, the NSR trains on single digits and correctly predicts numbers that are up to 14 orders of magnitude larger. This suggests that the NSR captures the true underlying arithmetic. In follow-up experiments, we use the NSR to control the computation of a downstream arithmetic unit to learn piecewise functions. We can also learn more challenging tasks through redundancy. Finally, we use the NSR to learn an upstream convolutional neural network to compare images of MNIST digits to decide which image contains the larger digit.