Preventing Representational Rank Collapse in MPNNs by Splitting the Computational Graph

The ability of message-passing neural networks (MPNNs) to fit complex functions over graphs is limited each iteration of message-passing over a simple makes representations more similar, a phenomenon known as rank collapse, and over-smoothing as a special case. Most approaches to mitigate over-smoothing extend common message-passing schemes, e.g., the graph convolutional network, by utilizing residual connections, gating mechanisms, normalization, or regularization techniques. Our work contrarily proposes to directly tackle the cause of this issue by modifying the message-passing scheme and exchanging different types of messages using multi-relational graphs. We identify the necessary and sufficient condition to ensure linearly independent node representations. As one instantion, we show that operating on multiple directed acyclic graphs always satisfies our condition and propose to obtain these by defining a strict partial ordering of the nodes. We conduct comprehensive experiments that confirm the benefits of operating on multi-relational graphs to achieve more informative node representations.

Simplifying the Theory on Over-Smoothing

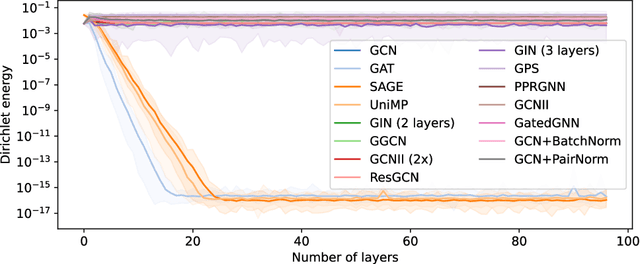
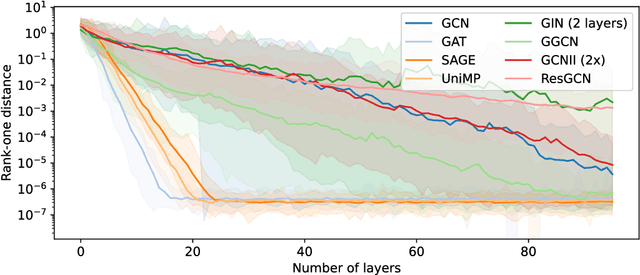
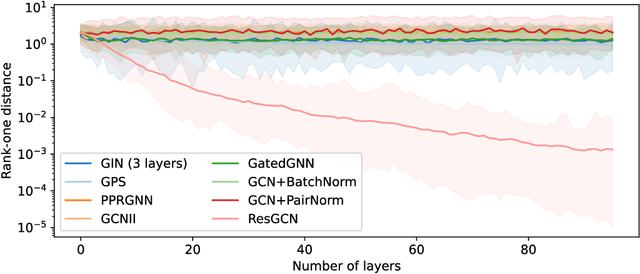
Graph convolutions have gained popularity due to their ability to efficiently operate on data with an irregular geometric structure. However, graph convolutions cause over-smoothing, which refers to representations becoming more similar with increased depth. However, many different definitions and intuitions currently coexist, leading to research efforts focusing on incompatible directions. This paper attempts to align these directions by showing that over-smoothing is merely a special case of power iteration. This greatly simplifies the existing theory on over-smoothing, making it more accessible. Based on the theory, we provide a novel comprehensive definition of rank collapse as a generalized form of over-smoothing and introduce the rank-one distance as a corresponding metric. Our empirical evaluation of 14 commonly used methods shows that more models than were previously known suffer from this issue.

Distilling Influences to Mitigate Prediction Churn in Graph Neural Networks

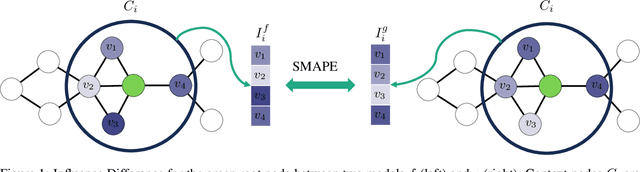
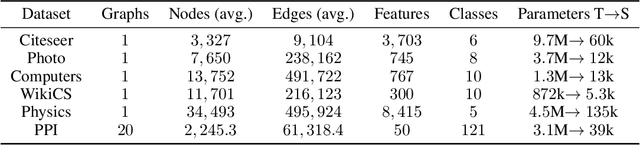
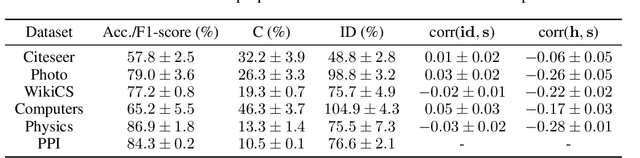
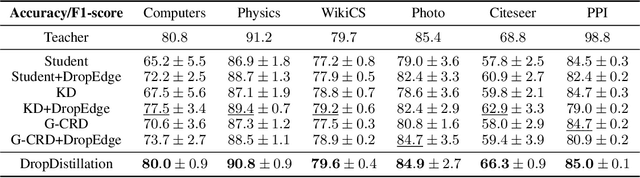
Models with similar performances exhibit significant disagreement in the predictions of individual samples, referred to as prediction churn. Our work explores this phenomenon in graph neural networks by investigating differences between models differing only in their initializations in their utilized features for predictions. We propose a novel metric called Influence Difference (ID) to quantify the variation in reasons used by nodes across models by comparing their influence distribution. Additionally, we consider the differences between nodes with a stable and an unstable prediction, positing that both equally utilize different reasons and thus provide a meaningful gradient signal to closely match two models even when the predictions for nodes are similar. Based on our analysis, we propose to minimize this ID in Knowledge Distillation, a domain where a new model should closely match an established one. As an efficient approximation, we introduce DropDistillation (DD) that matches the output for a graph perturbed by edge deletions. Our empirical evaluation of six benchmark datasets for node classification validates the differences in utilized features. DD outperforms previous methods regarding prediction stability and overall performance in all considered Knowledge Distillation experiments.

Rank Collapse Causes Over-Smoothing and Over-Correlation in Graph Neural Networks

Our study reveals new theoretical insights into over-smoothing and feature over-correlation in deep graph neural networks. We show the prevalence of invariant subspaces, demonstrating a fixed relative behavior that is unaffected by feature transformations. Our work clarifies recent observations related to convergence to a constant state and a potential over-separation of node states, as the amplification of subspaces only depends on the spectrum of the aggregation function. In linear scenarios, this leads to node representations being dominated by a low-dimensional subspace with an asymptotic convergence rate independent of the feature transformations. This causes a rank collapse of the node representations, resulting in over-smoothing when smooth vectors span this subspace, and over-correlation even when over-smoothing is avoided. Guided by our theory, we propose a sum of Kronecker products as a beneficial property that can provably prevent over-smoothing, over-correlation, and rank collapse. We empirically extend our insights to the non-linear case, demonstrating the inability of existing models to capture linearly independent features.

Curvature-based Pooling within Graph Neural Networks

Over-squashing and over-smoothing are two critical issues, that limit the capabilities of graph neural networks (GNNs). While over-smoothing eliminates the differences between nodes making them indistinguishable, over-squashing refers to the inability of GNNs to propagate information over long distances, as exponentially many node states are squashed into fixed-size representations. Both phenomena share similar causes, as both are largely induced by the graph topology. To mitigate these problems in graph classification tasks, we propose CurvPool, a novel pooling method. CurvPool exploits the notion of curvature of a graph to adaptively identify structures responsible for both over-smoothing and over-squashing. By clustering nodes based on the Balanced Forman curvature, CurvPool constructs a graph with a more suitable structure, allowing deeper models and the combination of distant information. We compare it to other state-of-the-art pooling approaches and establish its competitiveness in terms of classification accuracy, computational complexity, and flexibility. CurvPool outperforms several comparable methods across all considered tasks. The most consistent results are achieved by pooling densely connected clusters using the sum aggregation, as this allows additional information about the size of each pool.

Forecasting Unobserved Node States with spatio-temporal Graph Neural Networks

Forecasting future states of sensors is key to solving tasks like weather prediction, route planning, and many others when dealing with networks of sensors. But complete spatial coverage of sensors is generally unavailable and would practically be infeasible due to limitations in budget and other resources during deployment and maintenance. Currently existing approaches using machine learning are limited to the spatial locations where data was observed, causing limitations to downstream tasks. Inspired by the recent surge of Graph Neural Networks for spatio-temporal data processing, we investigate whether these can also forecast the state of locations with no sensors available. For this purpose, we develop a framework, named Forecasting Unobserved Node States (FUNS), that allows forecasting the state at entirely unobserved locations based on spatio-temporal correlations and the graph inductive bias. FUNS serves as a blueprint for optimizing models only on observed data and demonstrates good generalization capabilities for predicting the state at entirely unobserved locations during the testing stage. Our framework can be combined with any spatio-temporal Graph Neural Network, that exploits spatio-temporal correlations with surrounding observed locations by using the network's graph structure. Our employed model builds on a previous model by also allowing us to exploit prior knowledge about locations of interest, e.g. the road type. Our empirical evaluation of both simulated and real-world datasets demonstrates that Graph Neural Networks are well-suited for this task.

Transforming PageRank into an Infinite-Depth Graph Neural Network

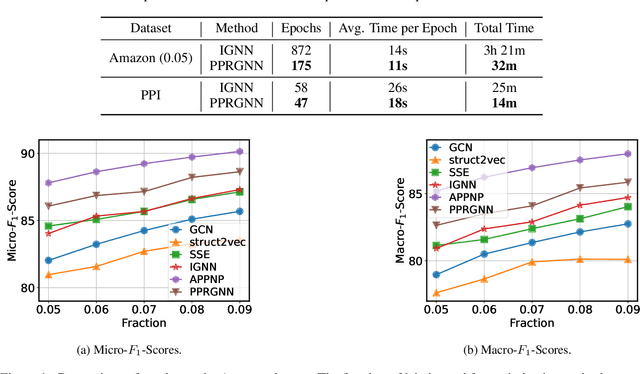
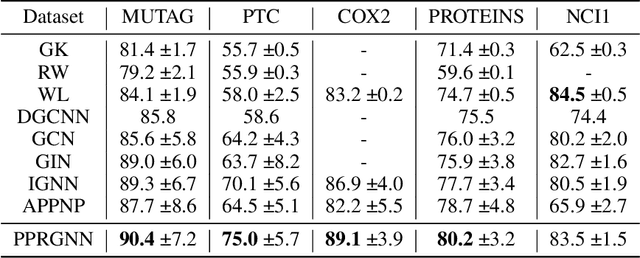
Popular graph neural networks are shallow models, despite the success of very deep architectures in other application domains of deep learning. This reduces the modeling capacity and leaves models unable to capture long-range relationships. The primary reason for the shallow design results from over-smoothing, which leads node states to become more similar with increased depth. We build on the close connection between GNNs and PageRank, for which personalized PageRank introduces the consideration of a personalization vector. Adopting this idea, we propose the Personalized PageRank Graph Neural Network (PPRGNN), which extends the graph convolutional network to an infinite-depth model that has a chance to reset the neighbor aggregation back to the initial state in each iteration. We introduce a nicely interpretable tweak to the chance of resetting and prove the convergence of our approach to a unique solution without placing any constraints, even when taking infinitely many neighbor aggregations. As in personalized PageRank, our result does not suffer from over-smoothing. While doing so, time complexity remains linear while we keep memory complexity constant, independently of the depth of the network, making it scale well to large graphs. We empirically show the effectiveness of our approach for various node and graph classification tasks. PPRGNN outperforms comparable methods in almost all cases.

Medley2K: A Dataset of Medley Transitions

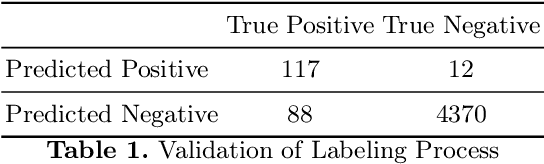
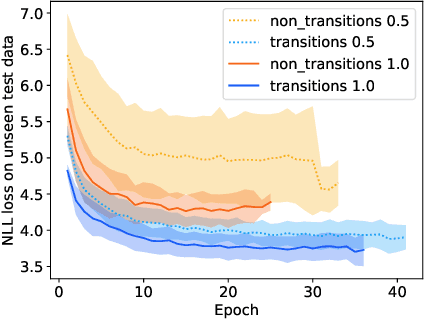
The automatic generation of medleys, i.e., musical pieces formed by different songs concatenated via smooth transitions, is not well studied in the current literature. To facilitate research on this topic, we make available a dataset called Medley2K that consists of 2,000 medleys and 7,712 labeled transitions. Our dataset features a rich variety of song transitions across different music genres. We provide a detailed description of this dataset and validate it by training a state-of-the-art generative model in the task of generating transitions between songs.