Simplifying the Theory on Over-Smoothing
Paper and Code
Jul 16, 2024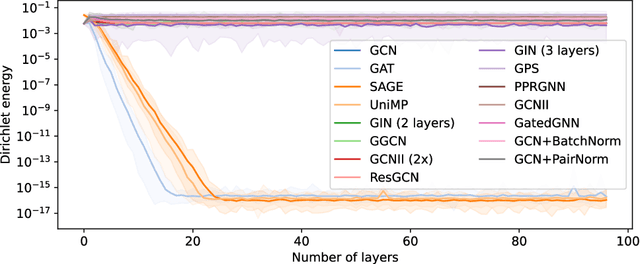
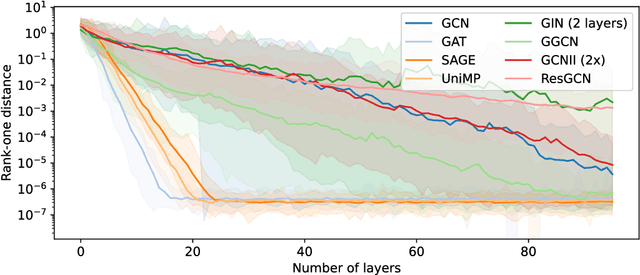
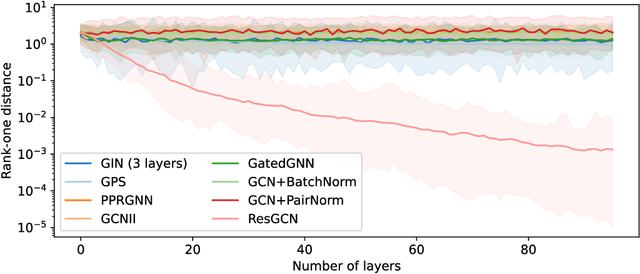
Graph convolutions have gained popularity due to their ability to efficiently operate on data with an irregular geometric structure. However, graph convolutions cause over-smoothing, which refers to representations becoming more similar with increased depth. However, many different definitions and intuitions currently coexist, leading to research efforts focusing on incompatible directions. This paper attempts to align these directions by showing that over-smoothing is merely a special case of power iteration. This greatly simplifies the existing theory on over-smoothing, making it more accessible. Based on the theory, we provide a novel comprehensive definition of rank collapse as a generalized form of over-smoothing and introduce the rank-one distance as a corresponding metric. Our empirical evaluation of 14 commonly used methods shows that more models than were previously known suffer from this issue.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge