Weisfeiler and Leman Go Gambling: Why Expressive Lottery Tickets Win

The lottery ticket hypothesis (LTH) is well-studied for convolutional neural networks but has been validated only empirically for graph neural networks (GNNs), for which theoretical findings are largely lacking. In this paper, we identify the expressivity of sparse subnetworks, i.e. their ability to distinguish non-isomorphic graphs, as crucial for finding winning tickets that preserve the predictive performance. We establish conditions under which the expressivity of a sparsely initialized GNN matches that of the full network, particularly when compared to the Weisfeiler-Leman test, and in that context put forward and prove a Strong Expressive Lottery Ticket Hypothesis. We subsequently show that an increased expressivity in the initialization potentially accelerates model convergence and improves generalization. Our findings establish novel theoretical foundations for both LTH and GNN research, highlighting the importance of maintaining expressivity in sparsely initialized GNNs. We illustrate our results using examples from drug discovery.

Preventing Representational Rank Collapse in MPNNs by Splitting the Computational Graph

The ability of message-passing neural networks (MPNNs) to fit complex functions over graphs is limited each iteration of message-passing over a simple makes representations more similar, a phenomenon known as rank collapse, and over-smoothing as a special case. Most approaches to mitigate over-smoothing extend common message-passing schemes, e.g., the graph convolutional network, by utilizing residual connections, gating mechanisms, normalization, or regularization techniques. Our work contrarily proposes to directly tackle the cause of this issue by modifying the message-passing scheme and exchanging different types of messages using multi-relational graphs. We identify the necessary and sufficient condition to ensure linearly independent node representations. As one instantion, we show that operating on multiple directed acyclic graphs always satisfies our condition and propose to obtain these by defining a strict partial ordering of the nodes. We conduct comprehensive experiments that confirm the benefits of operating on multi-relational graphs to achieve more informative node representations.

Non-Redundant Graph Neural Networks with Improved Expressiveness

Message passing graph neural networks iteratively compute node embeddings by aggregating messages from all neighbors. This procedure can be viewed as a neural variant of the Weisfeiler-Leman method, which limits their expressive power. Moreover, oversmoothing and oversquashing restrict the number of layers these networks can effectively utilize. The repeated exchange and encoding of identical information in message passing amplifies oversquashing. We propose a novel aggregation scheme based on neighborhood trees, which allows for controlling the redundancy by pruning branches of the unfolding trees underlying standard message passing. We prove that reducing redundancy improves expressivity and experimentally show that it alleviates oversquashing. We investigate the interaction between redundancy in message passing and redundancy in computation and propose a compact representation of neighborhood trees, from which we compute node and graph embeddings via a neural tree canonization technique. Our method is provably more expressive than the Weisfeiler-Leman method, less susceptible to oversquashing than message passing neural networks, and provides high classification accuracy on widely-used benchmark datasets.

Gradual Weisfeiler-Leman: Slow and Steady Wins the Race

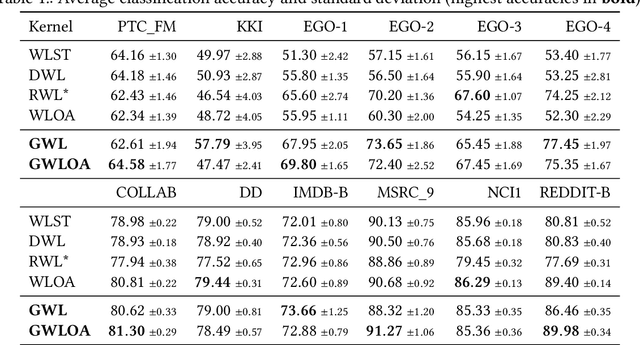
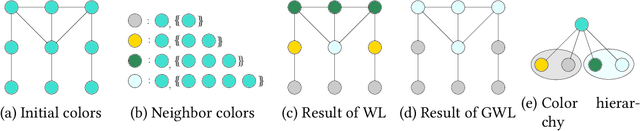
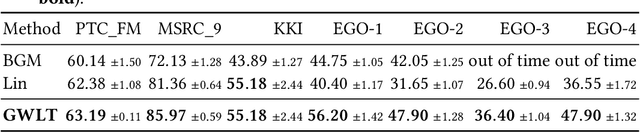
The classical Weisfeiler-Leman algorithm aka color refinement is fundamental for graph learning and central for successful graph kernels and graph neural networks. Originally developed for graph isomorphism testing, the algorithm iteratively refines vertex colors. On many datasets, the stable coloring is reached after a few iterations and the optimal number of iterations for machine learning tasks is typically even lower. This suggests that the colors diverge too fast, defining a similarity that is too coarse. We generalize the concept of color refinement and propose a framework for gradual neighborhood refinement, which allows a slower convergence to the stable coloring and thus provides a more fine-grained refinement hierarchy and vertex similarity. We assign new colors by clustering vertex neighborhoods, replacing the original injective color assignment function. Our approach is used to derive new variants of existing graph kernels and to approximate the graph edit distance via optimal assignments regarding vertex similarity. We show that in both tasks, our method outperforms the original color refinement with only moderate increase in running time advancing the state of the art.

TUDataset: A collection of benchmark datasets for learning with graphs

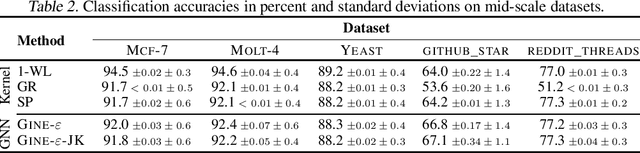
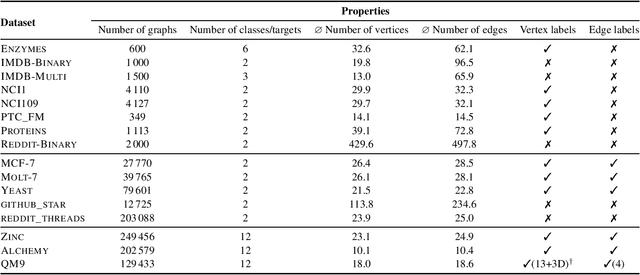
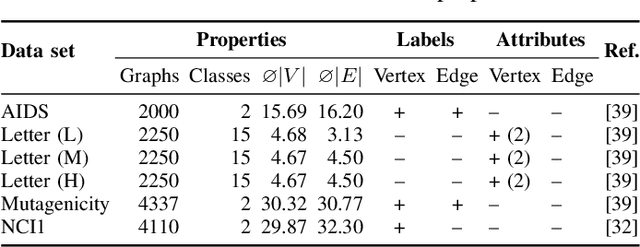
Recently, there has been an increasing interest in (supervised) learning with graph data, especially using graph neural networks. However, the development of meaningful benchmark datasets and standardized evaluation procedures is lagging, consequently hindering advancements in this area. To address this, we introduce the TUDataset for graph classification and regression. The collection consists of over 120 datasets of varying sizes from a wide range of applications. We provide Python-based data loaders, kernel and graph neural network baseline implementations, and evaluation tools. Here, we give an overview of the datasets, standardized evaluation procedures, and provide baseline experiments. All datasets are available at www.graphlearning.io. The experiments are fully reproducible from the code available at www.github.com/chrsmrrs/tudataset.

Computing Optimal Assignments in Linear Time for Graph Matching

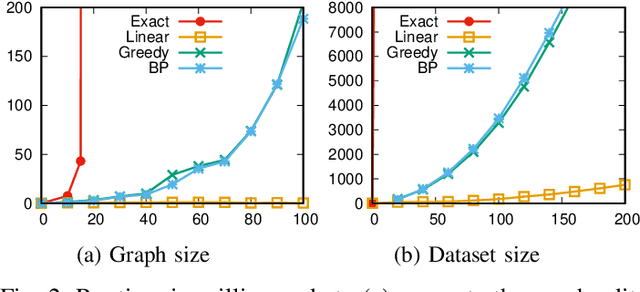
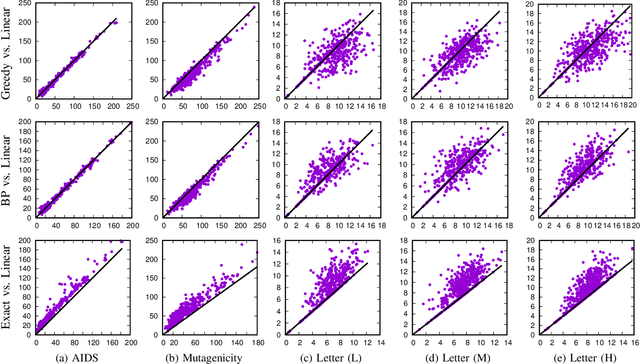
Finding an optimal assignment between two sets of objects is a fundamental problem arising in many applications, including the matching of `bag-of-words' representations in natural language processing and computer vision. Solving the assignment problem typically requires cubic time and its pairwise computation is expensive on large datasets. In this paper, we develop an algorithm which can find an optimal assignment in linear time when the cost function between objects is represented by a tree distance. We employ the method to approximate the edit distance between two graphs by matching their vertices in linear time. To this end, we propose two tree distances, the first of which reflects discrete and structural differences between vertices, and the second of which can be used to compare continuous labels. We verify the effectiveness and efficiency of our methods using synthetic and real-world datasets.