TUDataset: A collection of benchmark datasets for learning with graphs

Recently, there has been an increasing interest in (supervised) learning with graph data, especially using graph neural networks. However, the development of meaningful benchmark datasets and standardized evaluation procedures is lagging, consequently hindering advancements in this area. To address this, we introduce the TUDataset for graph classification and regression. The collection consists of over 120 datasets of varying sizes from a wide range of applications. We provide Python-based data loaders, kernel and graph neural network baseline implementations, and evaluation tools. Here, we give an overview of the datasets, standardized evaluation procedures, and provide baseline experiments. All datasets are available at www.graphlearning.io. The experiments are fully reproducible from the code available at www.github.com/chrsmrrs/tudataset.

A Unifying View of Explicit and Implicit Feature Maps for Structured Data: Systematic Studies of Graph Kernels

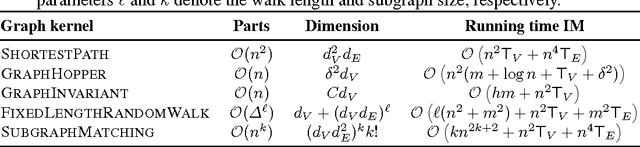
Non-linear kernel methods can be approximated by fast linear ones using suitable explicit feature maps allowing their application to large scale problems. To this end, explicit feature maps of kernels for vectorial data have been extensively studied. As many real-world data is structured, various kernels for complex data like graphs have been proposed. Indeed, many of them directly compute feature maps. However, the kernel trick is employed when the number of features is very large or the individual vertices of graphs are annotated by real-valued attributes. Can we still compute explicit feature maps efficiently under these circumstances? Triggered by this question, we investigate how general convolution kernels are composed from base kernels and construct corresponding feature maps. We apply our results to widely used graph kernels and analyze for which kernels and graph properties computation by explicit feature maps is feasible and actually more efficient. In particular, we derive feature maps for random walk and subgraph matching kernels and apply them to real-world graphs with discrete labels. Thereby, our theoretical results are confirmed experimentally by observing a phase transition when comparing running time with respect to label diversity, walk lengths and subgraph size, respectively. Moreover, we derive approximative, explicit feature maps for state-of-the-art kernels supporting real-valued attributes including the GraphHopper and Graph Invariant kernels. In extensive experiments we show that our approaches often achieve a classification accuracy close to the exact methods based on the kernel trick, but require only a fraction of their running time.

High-level Reasoning and Low-level Learning for Grasping: A Probabilistic Logic Pipeline

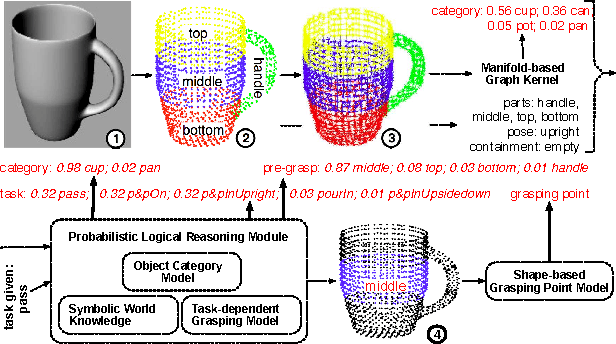
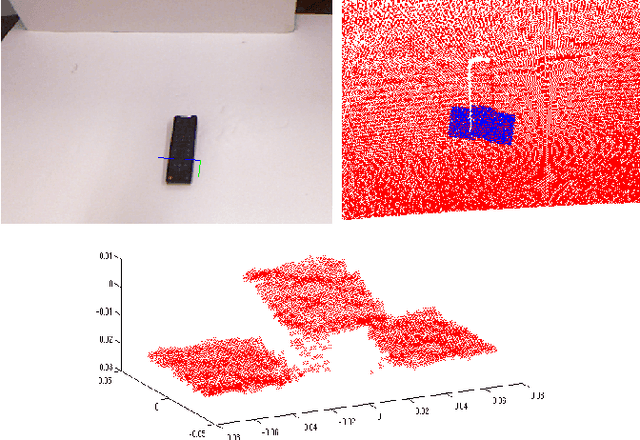
While grasps must satisfy the grasping stability criteria, good grasps depend on the specific manipulation scenario: the object, its properties and functionalities, as well as the task and grasp constraints. In this paper, we consider such information for robot grasping by leveraging manifolds and symbolic object parts. Specifically, we introduce a new probabilistic logic module to first semantically reason about pre-grasp configurations with respect to the intended tasks. Further, a mapping is learned from part-related visual features to good grasping points. The probabilistic logic module makes use of object-task affordances and object/task ontologies to encode rules that generalize over similar object parts and object/task categories. The use of probabilistic logic for task-dependent grasping contrasts with current approaches that usually learn direct mappings from visual perceptions to task-dependent grasping points. We show the benefits of the full probabilistic logic pipeline experimentally and on a real robot.

Propagation Kernels

We introduce propagation kernels, a general graph-kernel framework for efficiently measuring the similarity of structured data. Propagation kernels are based on monitoring how information spreads through a set of given graphs. They leverage early-stage distributions from propagation schemes such as random walks to capture structural information encoded in node labels, attributes, and edge information. This has two benefits. First, off-the-shelf propagation schemes can be used to naturally construct kernels for many graph types, including labeled, partially labeled, unlabeled, directed, and attributed graphs. Second, by leveraging existing efficient and informative propagation schemes, propagation kernels can be considerably faster than state-of-the-art approaches without sacrificing predictive performance. We will also show that if the graphs at hand have a regular structure, for instance when modeling image or video data, one can exploit this regularity to scale the kernel computation to large databases of graphs with thousands of nodes. We support our contributions by exhaustive experiments on a number of real-world graphs from a variety of application domains.