Petra Mutzel
TU Dortmund
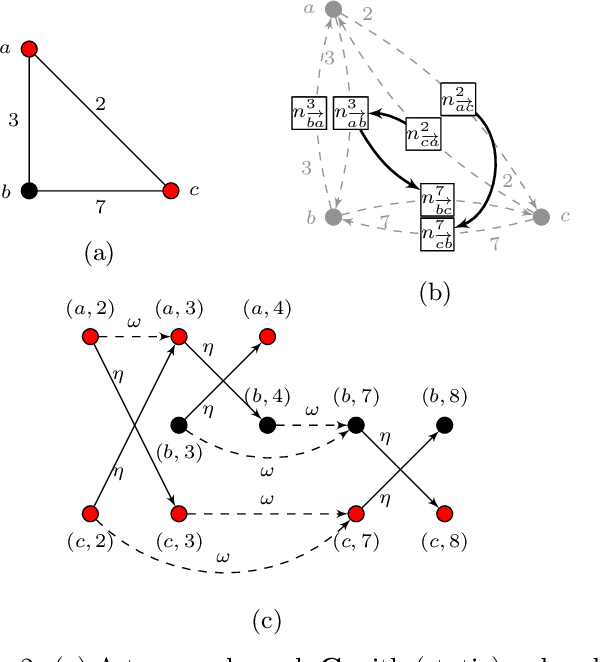
Weisfeiler and Leman Follow the Arrow of Time: Expressive Power of Message Passing in Temporal Event Graphs
May 30, 2025Abstract:An important characteristic of temporal graphs is how the directed arrow of time influences their causal topology, i.e., which nodes can possibly influence each other causally via time-respecting paths. The resulting patterns are often neglected by temporal graph neural networks (TGNNs). To formally analyze the expressive power of TGNNs, we lack a generalization of graph isomorphism to temporal graphs that fully captures their causal topology. Addressing this gap, we introduce the notion of consistent event graph isomorphism, which utilizes a time-unfolded representation of time-respecting paths in temporal graphs. We compare this definition with existing notions of temporal graph isomorphisms. We illustrate and highlight the advantages of our approach and develop a temporal generalization of the Weisfeiler-Leman algorithm to heuristically distinguish non-isomorphic temporal graphs. Building on this theoretical foundation, we derive a novel message passing scheme for temporal graph neural networks that operates on the event graph representation of temporal graphs. An experimental evaluation shows that our approach performs well in a temporal graph classification experiment.
A Customized SAT-based Solver for Graph Coloring
Apr 07, 2025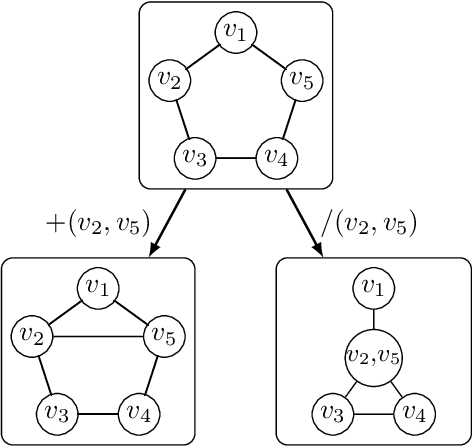
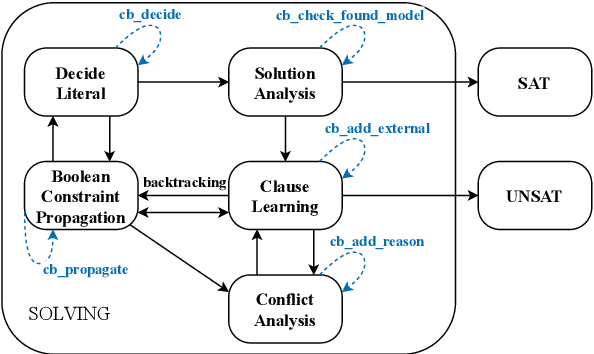

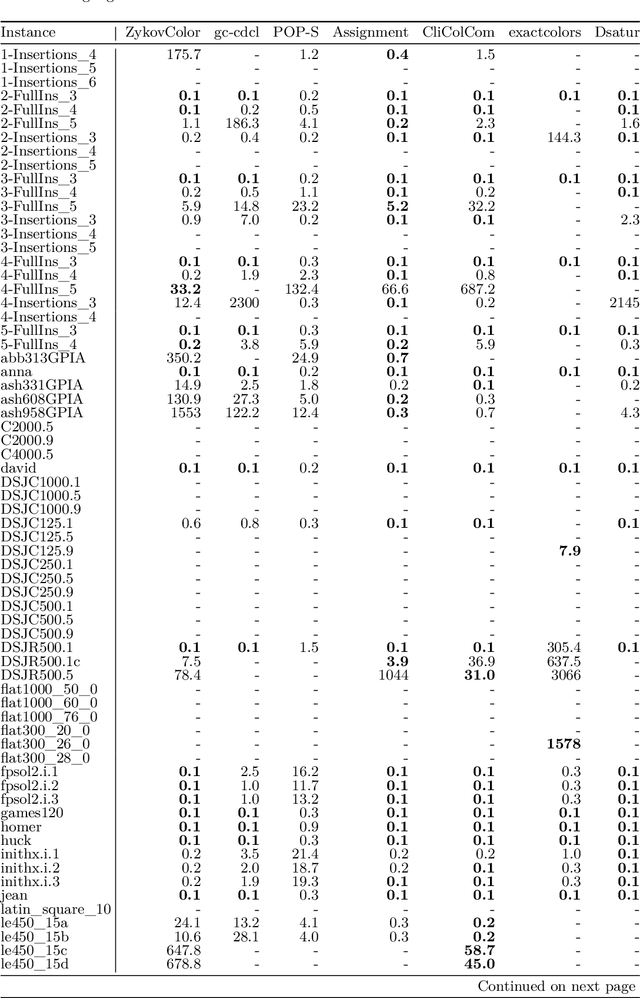
Abstract:We introduce ZykovColor, a novel SAT-based algorithm to solve the graph coloring problem working on top of an encoding that mimics the Zykov tree. Our method is based on an approach of H\'ebrard and Katsirelos (2020) that employs a propagator to enforce transitivity constraints, incorporate lower bounds for search tree pruning, and enable inferred propagations. We leverage the recently introduced IPASIR-UP interface for CaDiCal to implement these techniques with a SAT solver. Furthermore, we propose new features that take advantage of the underlying SAT solver. These include modifying the integrated decision strategy with vertex domination hints and using incremental bottom-up search that allows to reuse learned clauses from previous calls. Additionally, we integrate a more efficient clique computation to improve the lower bounds during the search. We validate the effectiveness of each new feature through an experimental analysis. ZykovColor outperforms other state-of-the-art graph coloring implementations on the DIMACS benchmark set. Further experiments on random Erd\H{o}s-R\'enyi graphs show that our new approach dominates state-of-the-art SAT-based methods for both very sparse and highly dense graphs.
SAT Encoding of Partial Ordering Models for Graph Coloring Problems
Mar 23, 2024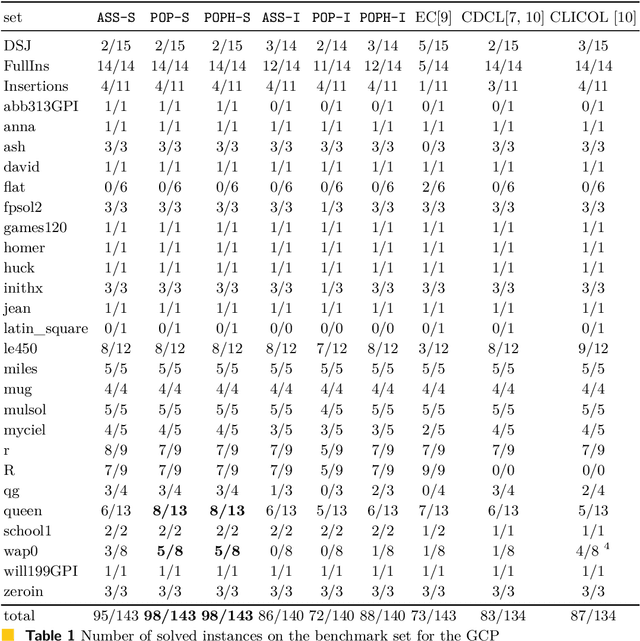
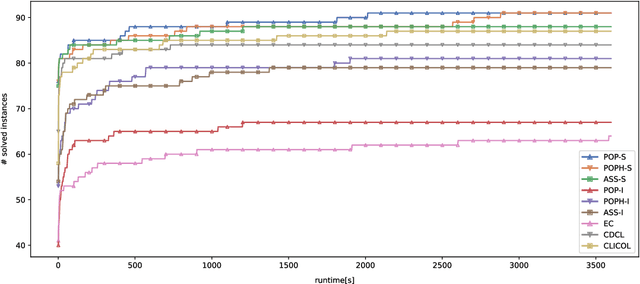
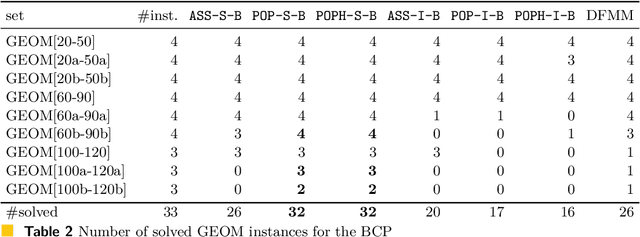
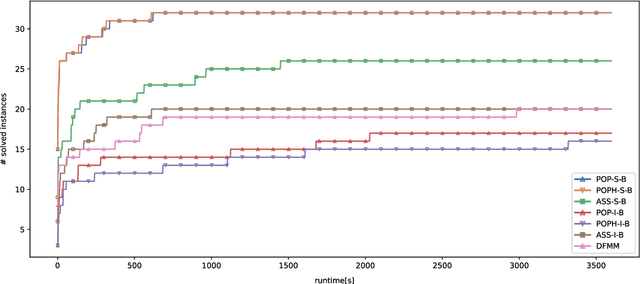
Abstract:In this paper, we suggest new SAT encodings of the partial-ordering based ILP model for the graph coloring problem (GCP) and the bandwidth coloring problem (BCP). The GCP asks for the minimum number of colors that can be assigned to the vertices of a given graph such that each two adjacent vertices get different colors. The BCP is a generalization, where each edge has a weight that enforces a minimal "distance" between the assigned colors, and the goal is to minimize the "largest" color used. For the widely studied GCP, we experimentally compare our new SAT encoding to the state-of-the-art approaches on the DIMACS benchmark set. Our evaluation confirms that this SAT encoding is effective for sparse graphs and even outperforms the state-of-the-art on some DIMACS instances. For the BCP, our theoretical analysis shows that the partial-ordering based SAT and ILP formulations have an asymptotically smaller size than that of the classical assignment-based model. Our practical evaluation confirms not only a dominance compared to the assignment-based encodings but also to the state-of-the-art approaches on a set of benchmark instances. Up to our knowledge, we have solved several open instances of the BCP from the literature for the first time.
A Temporal Graphlet Kernel for Classifying Dissemination in Evolving Networks
Sep 12, 2022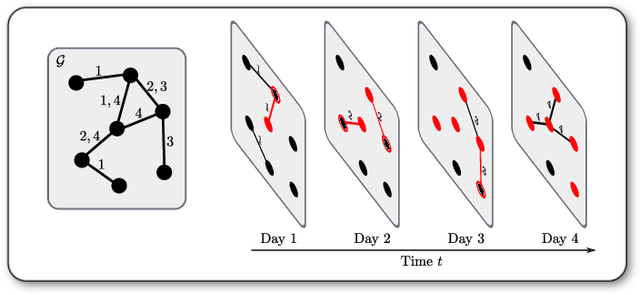
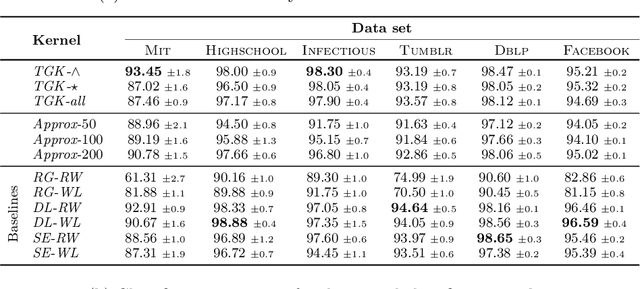


Abstract:We introduce the \emph{temporal graphlet kernel} for classifying dissemination processes in labeled temporal graphs. Such dissemination processes can be spreading (fake) news, infectious diseases, or computer viruses in dynamic networks. The networks are modeled as labeled temporal graphs, in which the edges exist at specific points in time, and node labels change over time. The classification problem asks to discriminate dissemination processes of different origins or parameters, e.g., infectious diseases with different infection probabilities. Our new kernel represents labeled temporal graphs in the feature space of temporal graphlets, i.e., small subgraphs distinguished by their structure, time-dependent node labels, and chronological order of edges. We introduce variants of our kernel based on classes of graphlets that are efficiently countable. For the case of temporal wedges, we propose a highly efficient approximative kernel with low error in expectation. We show that our kernels are faster to compute and provide better accuracy than state-of-the-art methods.
Temporal Walk Centrality: Ranking Nodes in Evolving Networks
Feb 08, 2022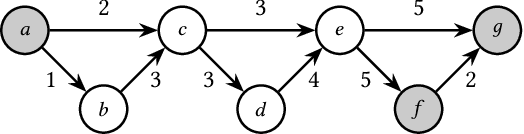
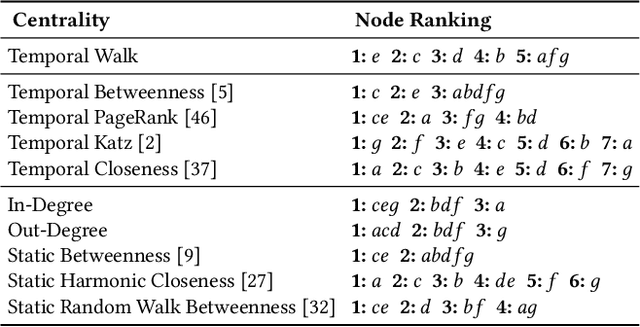
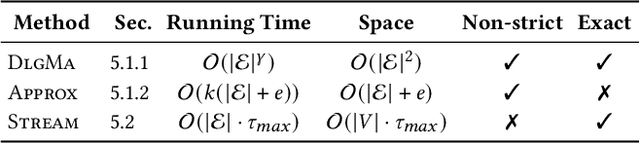
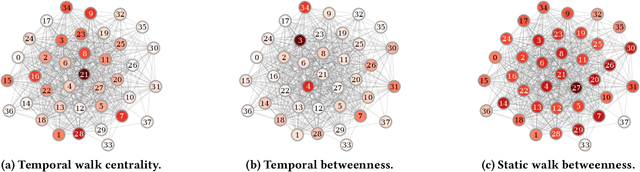
Abstract:We propose the Temporal Walk Centrality, which quantifies the importance of a node by measuring its ability to obtain and distribute information in a temporal network. In contrast to the widely-used betweenness centrality, we assume that information does not necessarily spread on shortest paths but on temporal random walks that satisfy the time constraints of the network. We show that temporal walk centrality can identify nodes playing central roles in dissemination processes that might not be detected by related betweenness concepts and other common static and temporal centrality measures. We propose exact and approximation algorithms with different running times depending on the properties of the temporal network and parameters of our new centrality measure. A technical contribution is a general approach to lift existing algebraic methods for counting walks in static networks to temporal networks. Our experiments on real-world temporal networks show the efficiency and accuracy of our algorithms. Finally, we demonstrate that the rankings by temporal walk centrality often differ significantly from those of other state-of-the-art temporal centralities.
TUDataset: A collection of benchmark datasets for learning with graphs
Jul 16, 2020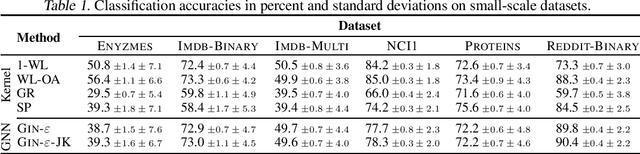
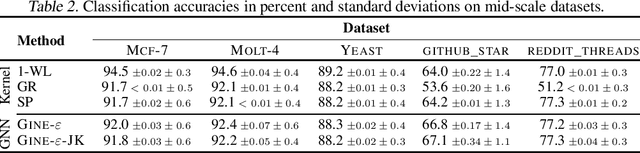

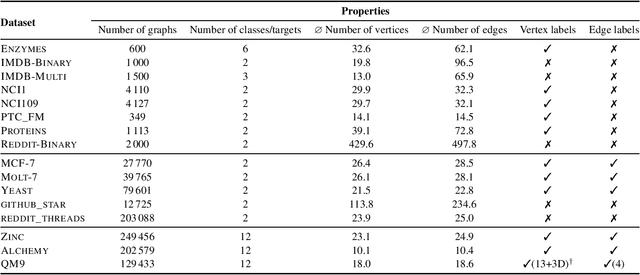
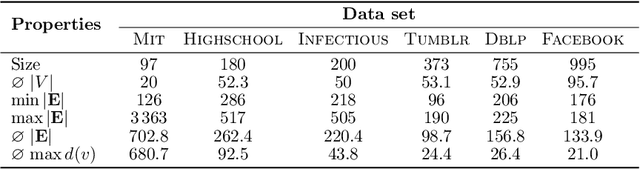
Abstract:Recently, there has been an increasing interest in (supervised) learning with graph data, especially using graph neural networks. However, the development of meaningful benchmark datasets and standardized evaluation procedures is lagging, consequently hindering advancements in this area. To address this, we introduce the TUDataset for graph classification and regression. The collection consists of over 120 datasets of varying sizes from a wide range of applications. We provide Python-based data loaders, kernel and graph neural network baseline implementations, and evaluation tools. Here, we give an overview of the datasets, standardized evaluation procedures, and provide baseline experiments. All datasets are available at www.graphlearning.io. The experiments are fully reproducible from the code available at www.github.com/chrsmrrs/tudataset.
Temporal Graph Kernels for Classifying Dissemination Processes
Oct 14, 2019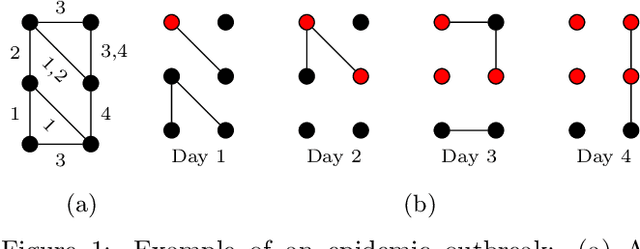

Abstract:Many real-world graphs or networks are temporal, e.g., in a social network persons only interact at specific points in time. This information directs dissemination processes on the network, such as the spread of rumors, fake news, or diseases. However, the current state-of-the-art methods for supervised graph classification are designed mainly for static graphs and may not be able to capture temporal information. Hence, they are not powerful enough to distinguish between graphs modeling different dissemination processes. To address this, we introduce a framework to lift standard graph kernels to the temporal domain. Specifically, we explore three different approaches and investigate the trade-offs between loss of temporal information and efficiency. Moreover, to handle large-scale graphs, we propose stochastic variants of our kernels with provable approximation guarantees. We evaluate our methods on a wide range of real-world social networks. Our methods beat static kernels by a large margin in terms of accuracy while still being scalable to large graphs and data sets. Hence, we confirm that taking temporal information into account is crucial for the successful classification of dissemination processes.
Towards a practical $k$-dimensional Weisfeiler-Leman algorithm
Apr 02, 2019



Abstract:The $k$-dimensional Weisfeiler-Leman algorithm is a well-known heuristic for the graph isomorphism problem. Moreover, it recently emerged as a powerful tool for supervised graph classification. The algorithm iteratively partitions the set of $k$-tuples, defined over the set of vertices of a graph, by considering neighboring $k$-tuples. Here, we propose a \new{local} variant which considers a subset of the original neighborhood in each iteration step. The cardinality of this local neighborhood, unlike the original one, only depends on the sparsity of the graph. Surprisingly, we show that the local variant has at least the same power as the original algorithm in terms of distinguishing non-isomorphic graphs. In order to demonstrate the practical utility of our local variant, we apply it to supervised graph classification. Our experimental study shows that our local algorithm leads to improved running times and classification accuracies on established benchmark datasets.
Recognizing Cuneiform Signs Using Graph Based Methods
Mar 09, 2018



Abstract:The cuneiform script constitutes one of the earliest systems of writing and is realized by wedge-shaped marks on clay tablets. A tremendous number of cuneiform tablets have already been discovered and are incrementally digitalized and made available to automated processing. As reading cuneiform script is still a manual task, we address the real-world application of recognizing cuneiform signs by two graph based methods with complementary runtime characteristics. We present a graph model for cuneiform signs together with a tailored distance measure based on the concept of the graph edit distance. We propose efficient heuristics for its computation and demonstrate its effectiveness in classification tasks experimentally. To this end, the distance measure is used to implement a nearest neighbor classifier leading to a high computational cost for the prediction phase with increasing training set size. In order to overcome this issue, we propose to use CNNs adapted to graphs as an alternative approach shifting the computational cost to the training phase. We demonstrate the practicability of both approaches in an extensive experimental comparison regarding runtime and prediction accuracy. Although currently available annotated real-world data is still limited, we obtain a high accuracy using CNNs, in particular, when the training set is enriched by augmented examples.
Global Weisfeiler-Lehman Graph Kernels
Sep 22, 2017

Abstract:Most state-of-the-art graph kernels only take local graph properties into account, i.e., the kernel is computed with regard to properties of the neighborhood of vertices or other small substructures. On the other hand, kernels that do take global graph propertiesinto account may not scale well to large graph databases. Here we propose to start exploring the space between local and global graph kernels, striking the balance between both worlds. Specifically, we introduce a novel graph kernel based on the $k$-dimensional Weisfeiler-Lehman algorithm. Unfortunately, the $k$-dimensional Weisfeiler-Lehman algorithm scales exponentially in $k$. Consequently, we devise a stochastic version of the kernel with provable approximation guarantees using conditional Rademacher averages. On bounded-degree graphs, it can even be computed in constant time. We support our theoretical results with experiments on several graph classification benchmarks, showing that our kernels often outperform the state-of-the-art in terms of classification accuracies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge