Top-k on a Budget: Adaptive Ranking with Weak and Strong Oracles

Identifying the top-$k$ items is fundamental but often prohibitive when exact valuations are expensive. We study a two-oracle setting with a fast, noisy weak oracle and a scarce, high-fidelity strong oracle (e.g., human expert verification or expensive simulation). We first analyze a simple screen-then-certify baseline (STC) and prove it makes at most $m(4\varepsilon_{\max})$ strong calls given jointly valid weak confidence intervals with maximum radius $\varepsilon_{\max}$, where $m(\cdot)$ denotes the near-tie mass around the top-$k$ threshold. We establish a conditional lower bound of $Ω(m(\varepsilon_{\max}))$ for any algorithm given the same weak uncertainty. Our main contribution is ACE, an adaptive certification algorithm that focuses strong queries on critical boundary items, achieving the same $O(m(4\varepsilon_{\max}))$ bound while reducing strong calls in practice. We then introduce ACE-W, a fully adaptive two-phase method that allocates weak budget adaptively before running ACE, further reducing strong costs.

Streaming Stochastic Submodular Maximization with On-Demand User Requests

We explore a novel problem in streaming submodular maximization, inspired by the dynamics of news-recommendation platforms. We consider a setting where users can visit a news website at any time, and upon each visit, the website must display up to $k$ news items. User interactions are inherently stochastic: each news item presented to the user is consumed with a certain acceptance probability by the user, and each news item covers certain topics. Our goal is to design a streaming algorithm that maximizes the expected total topic coverage. To address this problem, we establish a connection to submodular maximization subject to a matroid constraint. We show that we can effectively adapt previous methods to address our problem when the number of user visits is known in advance or linear-size memory in the stream length is available. However, in more realistic scenarios where only an upper bound on the visits and sublinear memory is available, the algorithms fail to guarantee any bounded performance. To overcome these limitations, we introduce a new online streaming algorithm that achieves a competitive ratio of $1/(8δ)$, where $δ$ controls the approximation quality. Moreover, it requires only a single pass over the stream, and uses memory independent of the stream length. Empirically, our algorithms consistently outperform the baselines.

A Temporal Graphlet Kernel for Classifying Dissemination in Evolving Networks

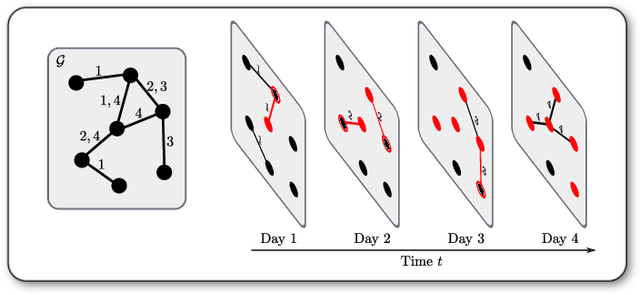
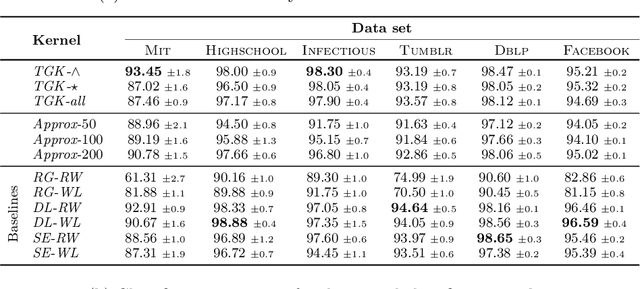
We introduce the \emph{temporal graphlet kernel} for classifying dissemination processes in labeled temporal graphs. Such dissemination processes can be spreading (fake) news, infectious diseases, or computer viruses in dynamic networks. The networks are modeled as labeled temporal graphs, in which the edges exist at specific points in time, and node labels change over time. The classification problem asks to discriminate dissemination processes of different origins or parameters, e.g., infectious diseases with different infection probabilities. Our new kernel represents labeled temporal graphs in the feature space of temporal graphlets, i.e., small subgraphs distinguished by their structure, time-dependent node labels, and chronological order of edges. We introduce variants of our kernel based on classes of graphlets that are efficiently countable. For the case of temporal wedges, we propose a highly efficient approximative kernel with low error in expectation. We show that our kernels are faster to compute and provide better accuracy than state-of-the-art methods.

Temporal Walk Centrality: Ranking Nodes in Evolving Networks

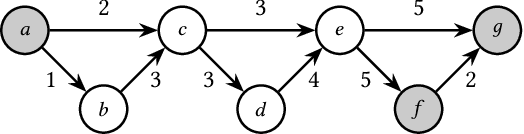
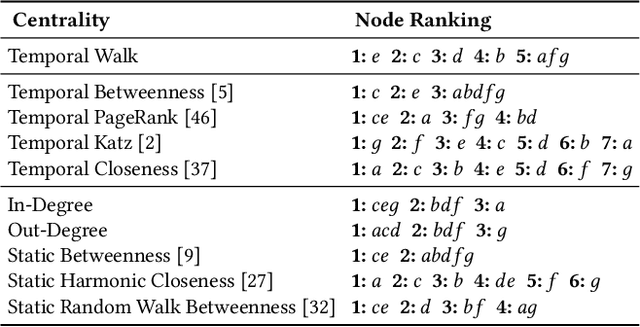
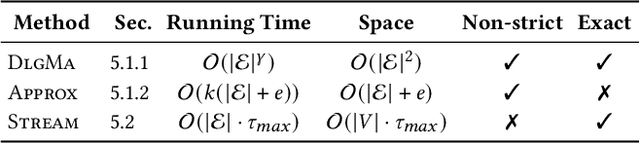
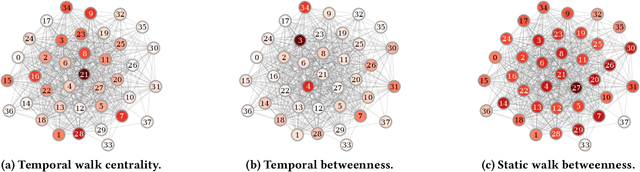
We propose the Temporal Walk Centrality, which quantifies the importance of a node by measuring its ability to obtain and distribute information in a temporal network. In contrast to the widely-used betweenness centrality, we assume that information does not necessarily spread on shortest paths but on temporal random walks that satisfy the time constraints of the network. We show that temporal walk centrality can identify nodes playing central roles in dissemination processes that might not be detected by related betweenness concepts and other common static and temporal centrality measures. We propose exact and approximation algorithms with different running times depending on the properties of the temporal network and parameters of our new centrality measure. A technical contribution is a general approach to lift existing algebraic methods for counting walks in static networks to temporal networks. Our experiments on real-world temporal networks show the efficiency and accuracy of our algorithms. Finally, we demonstrate that the rankings by temporal walk centrality often differ significantly from those of other state-of-the-art temporal centralities.

Temporal Graph Kernels for Classifying Dissemination Processes

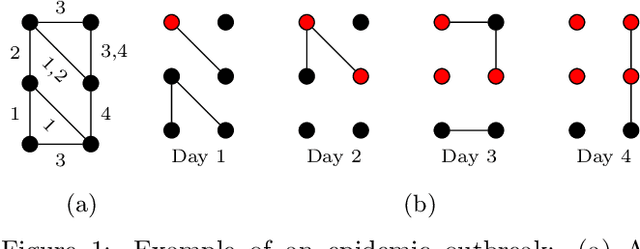
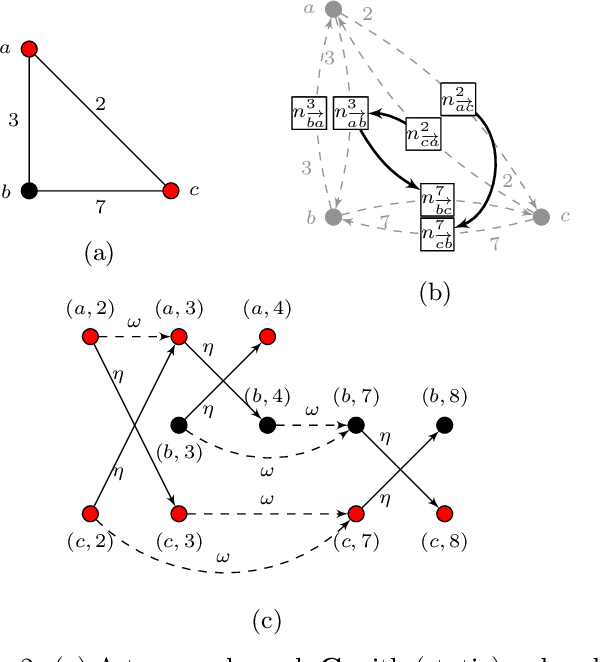
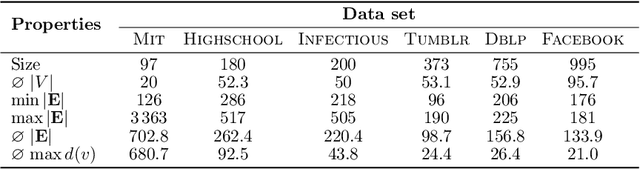
Many real-world graphs or networks are temporal, e.g., in a social network persons only interact at specific points in time. This information directs dissemination processes on the network, such as the spread of rumors, fake news, or diseases. However, the current state-of-the-art methods for supervised graph classification are designed mainly for static graphs and may not be able to capture temporal information. Hence, they are not powerful enough to distinguish between graphs modeling different dissemination processes. To address this, we introduce a framework to lift standard graph kernels to the temporal domain. Specifically, we explore three different approaches and investigate the trade-offs between loss of temporal information and efficiency. Moreover, to handle large-scale graphs, we propose stochastic variants of our kernels with provable approximation guarantees. We evaluate our methods on a wide range of real-world social networks. Our methods beat static kernels by a large margin in terms of accuracy while still being scalable to large graphs and data sets. Hence, we confirm that taking temporal information into account is crucial for the successful classification of dissemination processes.