Computing Optimal Assignments in Linear Time for Graph Matching

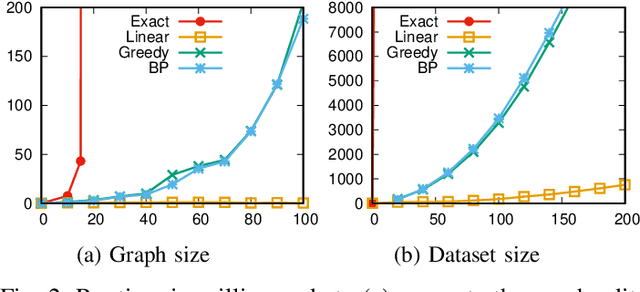
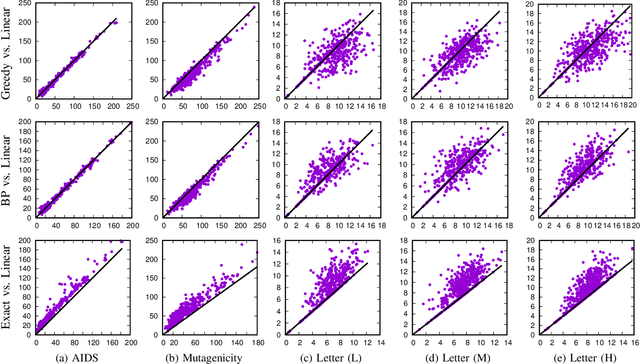
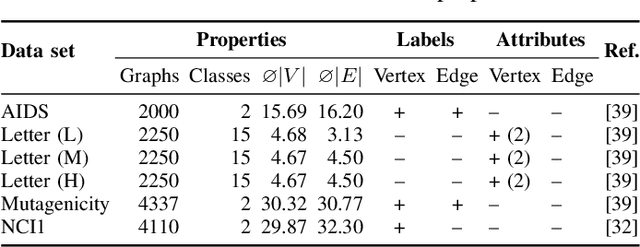
Finding an optimal assignment between two sets of objects is a fundamental problem arising in many applications, including the matching of `bag-of-words' representations in natural language processing and computer vision. Solving the assignment problem typically requires cubic time and its pairwise computation is expensive on large datasets. In this paper, we develop an algorithm which can find an optimal assignment in linear time when the cost function between objects is represented by a tree distance. We employ the method to approximate the edit distance between two graphs by matching their vertices in linear time. To this end, we propose two tree distances, the first of which reflects discrete and structural differences between vertices, and the second of which can be used to compare continuous labels. We verify the effectiveness and efficiency of our methods using synthetic and real-world datasets.

On Valid Optimal Assignment Kernels and Applications to Graph Classification

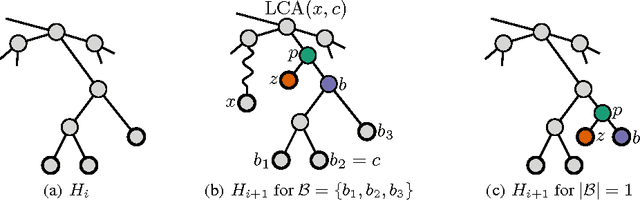
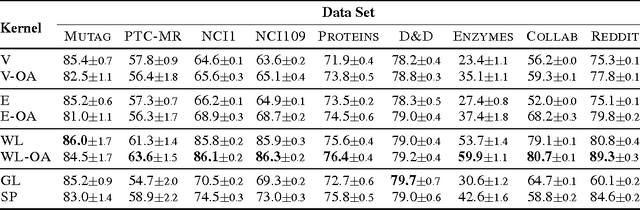
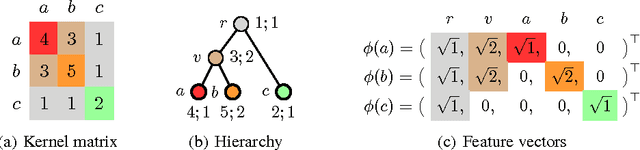
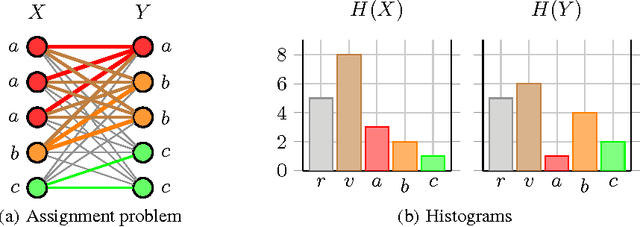
The success of kernel methods has initiated the design of novel positive semidefinite functions, in particular for structured data. A leading design paradigm for this is the convolution kernel, which decomposes structured objects into their parts and sums over all pairs of parts. Assignment kernels, in contrast, are obtained from an optimal bijection between parts, which can provide a more valid notion of similarity. In general however, optimal assignments yield indefinite functions, which complicates their use in kernel methods. We characterize a class of base kernels used to compare parts that guarantees positive semidefinite optimal assignment kernels. These base kernels give rise to hierarchies from which the optimal assignment kernels are computed in linear time by histogram intersection. We apply these results by developing the Weisfeiler-Lehman optimal assignment kernel for graphs. It provides high classification accuracy on widely-used benchmark data sets improving over the original Weisfeiler-Lehman kernel.