Generalizing to any diverse distribution: uniformity, gentle finetuning and rebalancing

As training datasets grow larger, we aspire to develop models that generalize well to any diverse test distribution, even if the latter deviates significantly from the training data. Various approaches like domain adaptation, domain generalization, and robust optimization attempt to address the out-of-distribution challenge by posing assumptions about the relation between training and test distribution. Differently, we adopt a more conservative perspective by accounting for the worst-case error across all sufficiently diverse test distributions within a known domain. Our first finding is that training on a uniform distribution over this domain is optimal. We also interrogate practical remedies when uniform samples are unavailable by considering methods for mitigating non-uniformity through finetuning and rebalancing. Our theory provides a mathematical grounding for previous observations on the role of entropy and rebalancing for o.o.d. generalization and foundation model training. We also provide new empirical evidence across tasks involving o.o.d. shifts which illustrate the broad applicability of our perspective.

Batch Selection for Parallelisation of Bayesian Quadrature

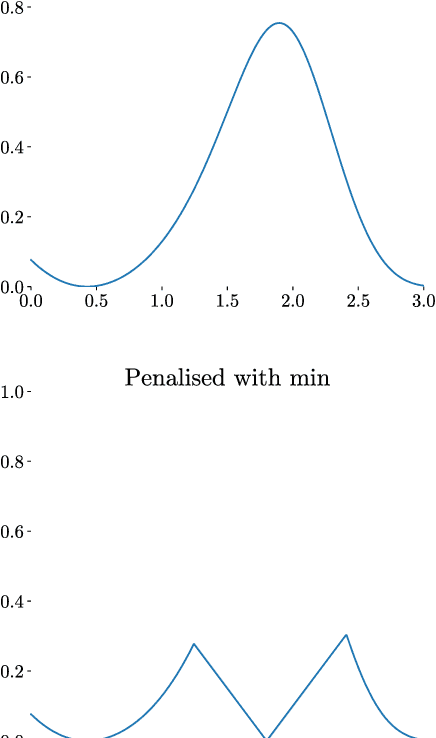
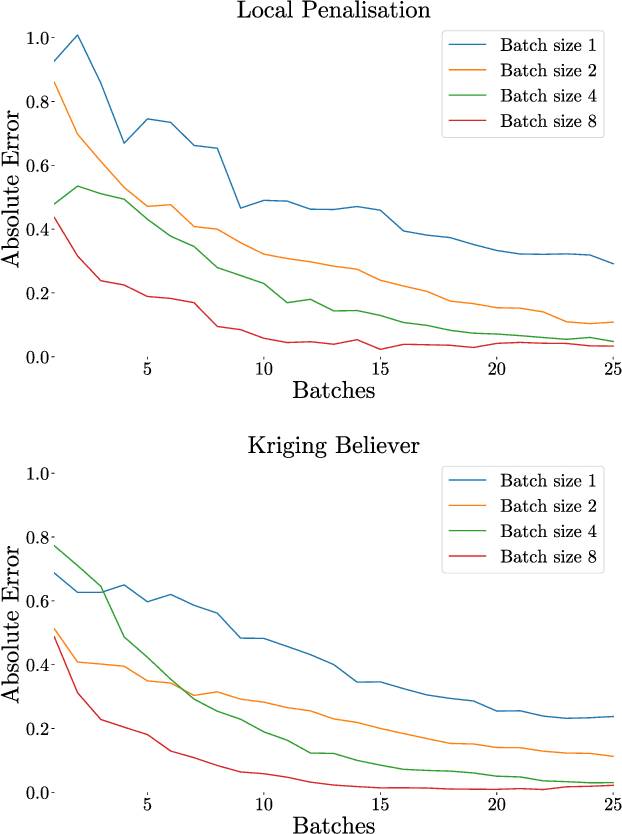
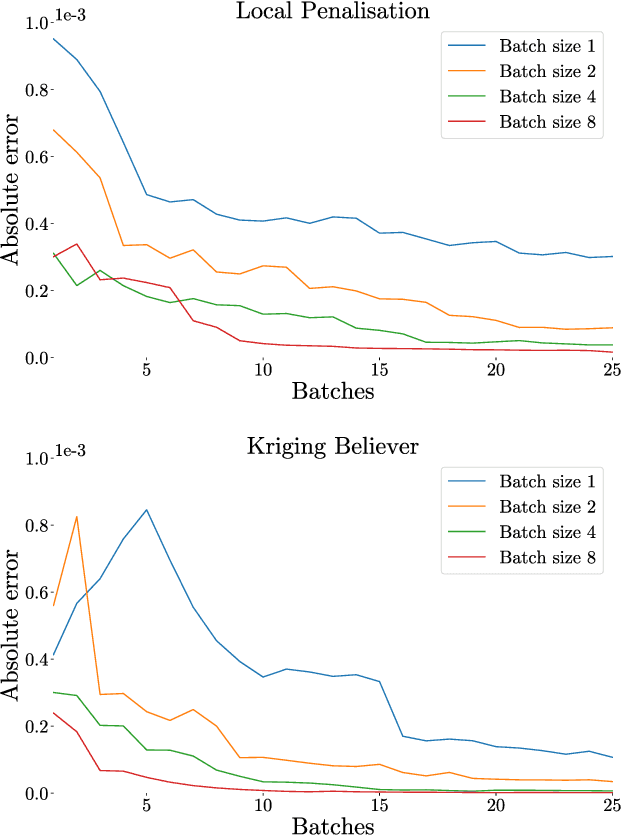
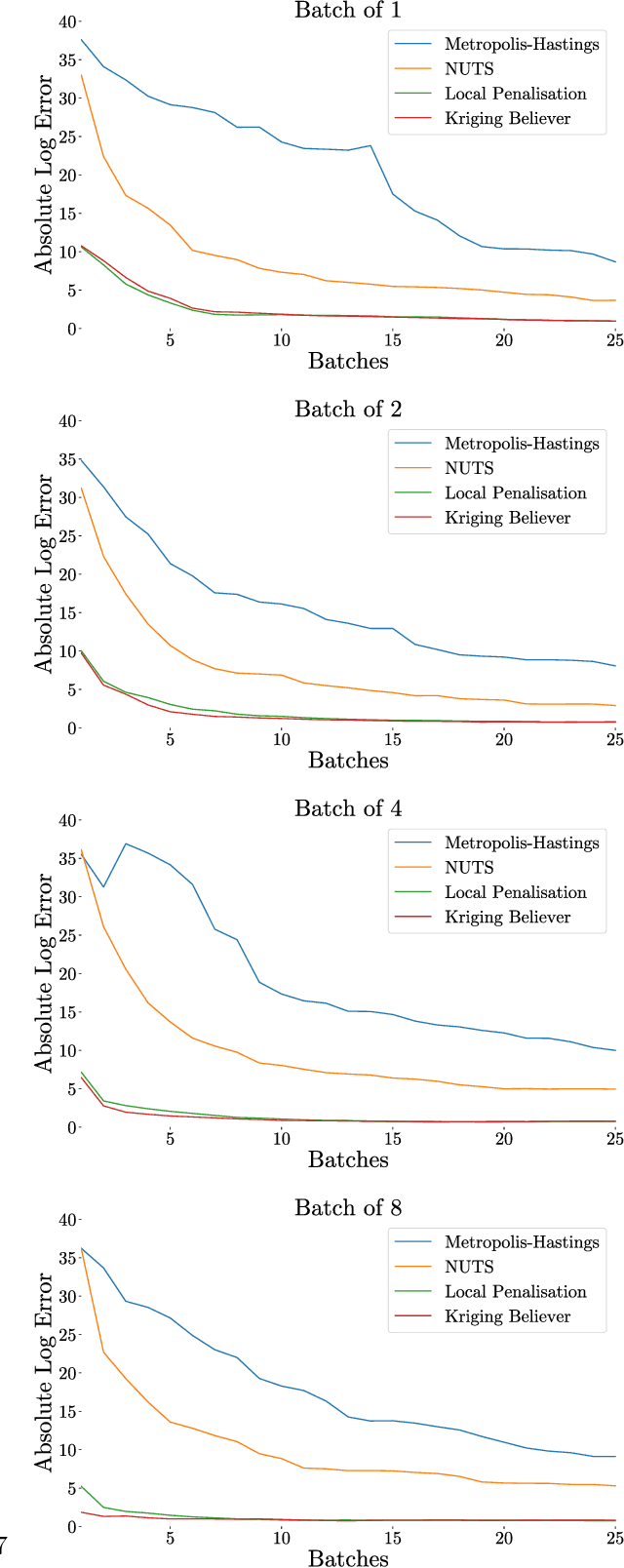
Integration over non-negative integrands is a central problem in machine learning (e.g. for model averaging, (hyper-)parameter marginalisation, and computing posterior predictive distributions). Bayesian Quadrature is a probabilistic numerical integration technique that performs promisingly when compared to traditional Markov Chain Monte Carlo methods. However, in contrast to easily-parallelised MCMC methods, Bayesian Quadrature methods have, thus far, been essentially serial in nature, selecting a single point to sample at each step of the algorithm. We deliver methods to select batches of points at each step, based upon those recently presented in the Batch Bayesian Optimisation literature. Such parallelisation significantly reduces computation time, especially when the integrand is expensive to sample.