Generalizing to any diverse distribution: uniformity, gentle finetuning and rebalancing

As training datasets grow larger, we aspire to develop models that generalize well to any diverse test distribution, even if the latter deviates significantly from the training data. Various approaches like domain adaptation, domain generalization, and robust optimization attempt to address the out-of-distribution challenge by posing assumptions about the relation between training and test distribution. Differently, we adopt a more conservative perspective by accounting for the worst-case error across all sufficiently diverse test distributions within a known domain. Our first finding is that training on a uniform distribution over this domain is optimal. We also interrogate practical remedies when uniform samples are unavailable by considering methods for mitigating non-uniformity through finetuning and rebalancing. Our theory provides a mathematical grounding for previous observations on the role of entropy and rebalancing for o.o.d. generalization and foundation model training. We also provide new empirical evidence across tasks involving o.o.d. shifts which illustrate the broad applicability of our perspective.

Implicitly Guided Design with PropEn: Match your Data to Follow the Gradient

Across scientific domains, generating new models or optimizing existing ones while meeting specific criteria is crucial. Traditional machine learning frameworks for guided design use a generative model and a surrogate model (discriminator), requiring large datasets. However, real-world scientific applications often have limited data and complex landscapes, making data-hungry models inefficient or impractical. We propose a new framework, PropEn, inspired by ``matching'', which enables implicit guidance without training a discriminator. By matching each sample with a similar one that has a better property value, we create a larger training dataset that inherently indicates the direction of improvement. Matching, combined with an encoder-decoder architecture, forms a domain-agnostic generative framework for property enhancement. We show that training with a matched dataset approximates the gradient of the property of interest while remaining within the data distribution, allowing efficient design optimization. Extensive evaluations in toy problems and scientific applications, such as therapeutic protein design and airfoil optimization, demonstrate PropEn's advantages over common baselines. Notably, the protein design results are validated with wet lab experiments, confirming the competitiveness and effectiveness of our approach.

AbDiffuser: Full-Atom Generation of In-Vitro Functioning Antibodies

We introduce AbDiffuser, an equivariant and physics-informed diffusion model for the joint generation of antibody 3D structures and sequences. AbDiffuser is built on top of a new representation of protein structure, relies on a novel architecture for aligned proteins, and utilizes strong diffusion priors to improve the denoising process. Our approach improves protein diffusion by taking advantage of domain knowledge and physics-based constraints; handles sequence-length changes; and reduces memory complexity by an order of magnitude enabling backbone and side chain generation. We validate AbDiffuser in silico and in vitro. Numerical experiments showcase the ability of AbDiffuser to generate antibodies that closely track the sequence and structural properties of a reference set. Laboratory experiments confirm that all 16 HER2 antibodies discovered were expressed at high levels and that 57.1% of selected designs were tight binders.

Batched Predictors Generalize within Distribution

We study the generalization properties of batched predictors, i.e., models tasked with predicting the mean label of a small set (or batch) of examples. The batched prediction paradigm is particularly relevant for models deployed to determine the quality of a group of compounds in preparation for offline testing. By utilizing a suitable generalization of the Rademacher complexity, we prove that batched predictors come with exponentially stronger generalization guarantees as compared to the standard per-sample approach. Surprisingly, the proposed bound holds independently of overparametrization. Our theoretical insights are validated experimentally for various tasks, architectures, and applications.

Protein Discovery with Discrete Walk-Jump Sampling

We resolve difficulties in training and sampling from a discrete generative model by learning a smoothed energy function, sampling from the smoothed data manifold with Langevin Markov chain Monte Carlo (MCMC), and projecting back to the true data manifold with one-step denoising. Our Discrete Walk-Jump Sampling formalism combines the maximum likelihood training of an energy-based model and improved sample quality of a score-based model, while simplifying training and sampling by requiring only a single noise level. We evaluate the robustness of our approach on generative modeling of antibody proteins and introduce the distributional conformity score to benchmark protein generative models. By optimizing and sampling from our models for the proposed distributional conformity score, 97-100% of generated samples are successfully expressed and purified and 35% of functional designs show equal or improved binding affinity compared to known functional antibodies on the first attempt in a single round of laboratory experiments. We also report the first demonstration of long-run fast-mixing MCMC chains where diverse antibody protein classes are visited in a single MCMC chain.

Infusing Lattice Symmetry Priors in Attention Mechanisms for Sample-Efficient Abstract Geometric Reasoning

The Abstraction and Reasoning Corpus (ARC) (Chollet, 2019) and its most recent language-complete instantiation (LARC) has been postulated as an important step towards general AI. Yet, even state-of-the-art machine learning models struggle to achieve meaningful performance on these problems, falling behind non-learning based approaches. We argue that solving these tasks requires extreme generalization that can only be achieved by proper accounting for core knowledge priors. As a step towards this goal, we focus on geometry priors and introduce LatFormer, a model that incorporates lattice symmetry priors in attention masks. We show that, for any transformation of the hypercubic lattice, there exists a binary attention mask that implements that group action. Hence, our study motivates a modification to the standard attention mechanism, where attention weights are scaled using soft masks generated by a convolutional network. Experiments on synthetic geometric reasoning show that LatFormer requires 2 orders of magnitude fewer data than standard attention and transformers. Moreover, our results on ARC and LARC tasks that incorporate geometric priors provide preliminary evidence that these complex datasets do not lie out of the reach of deep learning models.

Towards Understanding and Improving GFlowNet Training

Generative flow networks (GFlowNets) are a family of algorithms that learn a generative policy to sample discrete objects $x$ with non-negative reward $R(x)$. Learning objectives guarantee the GFlowNet samples $x$ from the target distribution $p^*(x) \propto R(x)$ when loss is globally minimized over all states or trajectories, but it is unclear how well they perform with practical limits on training resources. We introduce an efficient evaluation strategy to compare the learned sampling distribution to the target reward distribution. As flows can be underdetermined given training data, we clarify the importance of learned flows to generalization and matching $p^*(x)$ in practice. We investigate how to learn better flows, and propose (i) prioritized replay training of high-reward $x$, (ii) relative edge flow policy parametrization, and (iii) a novel guided trajectory balance objective, and show how it can solve a substructure credit assignment problem. We substantially improve sample efficiency on biochemical design tasks.

A Pareto-optimal compositional energy-based model for sampling and optimization of protein sequences

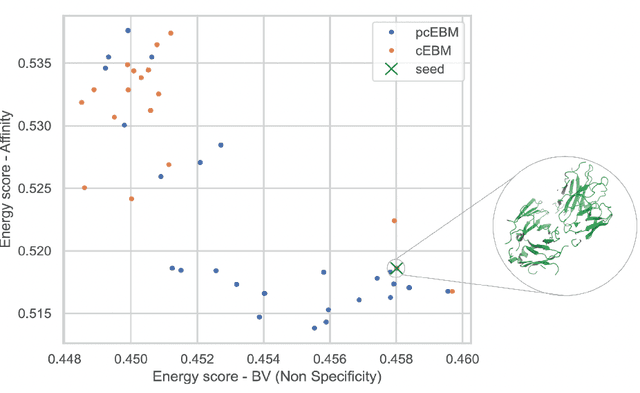
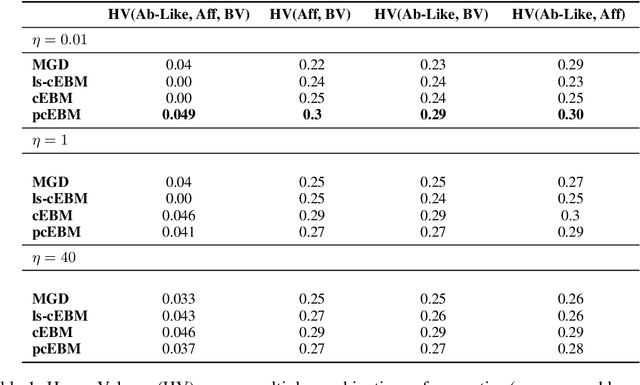
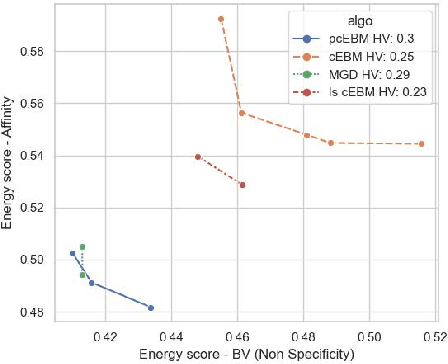
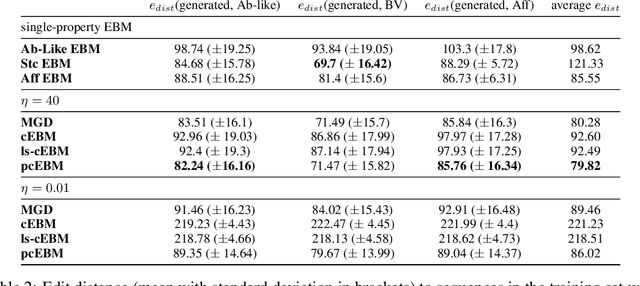
Deep generative models have emerged as a popular machine learning-based approach for inverse design problems in the life sciences. However, these problems often require sampling new designs that satisfy multiple properties of interest in addition to learning the data distribution. This multi-objective optimization becomes more challenging when properties are independent or orthogonal to each other. In this work, we propose a Pareto-compositional energy-based model (pcEBM), a framework that uses multiple gradient descent for sampling new designs that adhere to various constraints in optimizing distinct properties. We demonstrate its ability to learn non-convex Pareto fronts and generate sequences that simultaneously satisfy multiple desired properties across a series of real-world antibody design tasks.

On the generalization of learning algorithms that do not converge

Generalization analyses of deep learning typically assume that the training converges to a fixed point. But, recent results indicate that in practice, the weights of deep neural networks optimized with stochastic gradient descent often oscillate indefinitely. To reduce this discrepancy between theory and practice, this paper focuses on the generalization of neural networks whose training dynamics do not necessarily converge to fixed points. Our main contribution is to propose a notion of statistical algorithmic stability (SAS) that extends classical algorithmic stability to non-convergent algorithms and to study its connection to generalization. This ergodic-theoretic approach leads to new insights when compared to the traditional optimization and learning theory perspectives. We prove that the stability of the time-asymptotic behavior of a learning algorithm relates to its generalization and empirically demonstrate how loss dynamics can provide clues to generalization performance. Our findings provide evidence that networks that "train stably generalize better" even when the training continues indefinitely and the weights do not converge.

Neural Set Function Extensions: Learning with Discrete Functions in High Dimensions

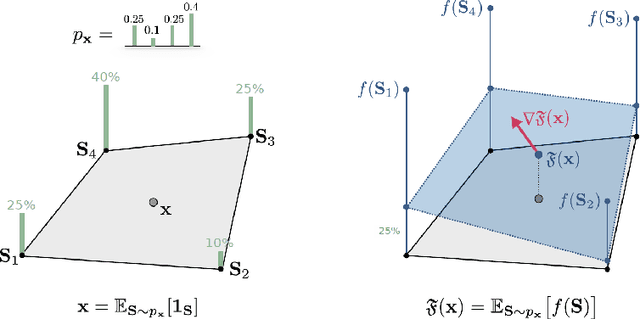
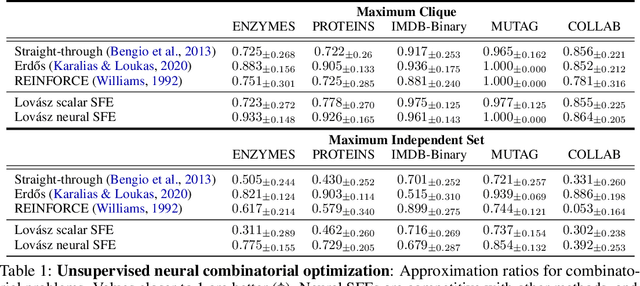
Integrating functions on discrete domains into neural networks is key to developing their capability to reason about discrete objects. But, discrete domains are (1) not naturally amenable to gradient-based optimization, and (2) incompatible with deep learning architectures that rely on representations in high-dimensional vector spaces. In this work, we address both difficulties for set functions, which capture many important discrete problems. First, we develop a framework for extending set functions onto low-dimensional continuous domains, where many extensions are naturally defined. Our framework subsumes many well-known extensions as special cases. Second, to avoid undesirable low-dimensional neural network bottlenecks, we convert low-dimensional extensions into representations in high-dimensional spaces, taking inspiration from the success of semidefinite programs for combinatorial optimization. Empirically, we observe benefits of our extensions for unsupervised neural combinatorial optimization, in particular with high-dimensional representations.