Equivariant Neural Tangent Kernels

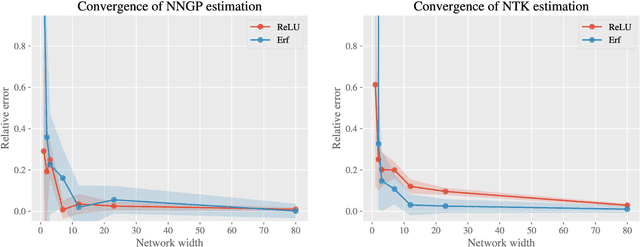
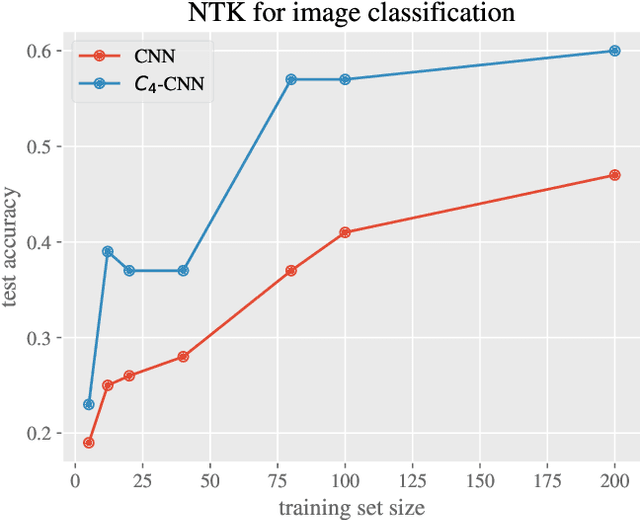
Equivariant neural networks have in recent years become an important technique for guiding architecture selection for neural networks with many applications in domains ranging from medical image analysis to quantum chemistry. In particular, as the most general linear equivariant layers with respect to the regular representation, group convolutions have been highly impactful in numerous applications. Although equivariant architectures have been studied extensively, much less is known about the training dynamics of equivariant neural networks. Concurrently, neural tangent kernels (NTKs) have emerged as a powerful tool to analytically understand the training dynamics of wide neural networks. In this work, we combine these two fields for the first time by giving explicit expressions for NTKs of group convolutional neural networks. In numerical experiments, we demonstrate superior performance for equivariant NTKs over non-equivariant NTKs on a classification task for medical images.

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.

Fast and Unified Path Gradient Estimators for Normalizing Flows

Recent work shows that path gradient estimators for normalizing flows have lower variance compared to standard estimators for variational inference, resulting in improved training. However, they are often prohibitively more expensive from a computational point of view and cannot be applied to maximum likelihood training in a scalable manner, which severely hinders their widespread adoption. In this work, we overcome these crucial limitations. Specifically, we propose a fast path gradient estimator which improves computational efficiency significantly and works for all normalizing flow architectures of practical relevance. We then show that this estimator can also be applied to maximum likelihood training for which it has a regularizing effect as it can take the form of a given target energy function into account. We empirically establish its superior performance and reduced variance for several natural sciences applications.

Emergent Equivariance in Deep Ensembles

We demonstrate that deep ensembles are secretly equivariant models. More precisely, we show that deep ensembles become equivariant for all inputs and at all training times by simply using data augmentation. Crucially, equivariance holds off-manifold and for any architecture in the infinite width limit. The equivariance is emergent in the sense that predictions of individual ensemble members are not equivariant but their collective prediction is. Neural tangent kernel theory is used to derive this result and we verify our theoretical insights using detailed numerical experiments.

Batched Predictors Generalize within Distribution

We study the generalization properties of batched predictors, i.e., models tasked with predicting the mean label of a small set (or batch) of examples. The batched prediction paradigm is particularly relevant for models deployed to determine the quality of a group of compounds in preparation for offline testing. By utilizing a suitable generalization of the Rademacher complexity, we prove that batched predictors come with exponentially stronger generalization guarantees as compared to the standard per-sample approach. Surprisingly, the proposed bound holds independently of overparametrization. Our theoretical insights are validated experimentally for various tasks, architectures, and applications.

Detecting and Mitigating Mode-Collapse for Flow-based Sampling of Lattice Field Theories

We study the consequences of mode-collapse of normalizing flows in the context of lattice field theory. Normalizing flows allow for independent sampling. For this reason, it is hoped that they can avoid the tunneling problem of local-update MCMC algorithms for multi-modal distributions. In this work, we first point out that the tunneling problem is also present for normalizing flows but is shifted from the sampling to the training phase of the algorithm. Specifically, normalizing flows often suffer from mode-collapse for which the training process assigns vanishingly low probability mass to relevant modes of the physical distribution. This may result in a significant bias when the flow is used as a sampler in a Markov-Chain or with Importance Sampling. We propose a metric to quantify the degree of mode-collapse and derive a bound on the resulting bias. Furthermore, we propose various mitigation strategies in particular in the context of estimating thermodynamic observables, such as the free energy.

Gradients should stay on Path: Better Estimators of the Reverse- and Forward KL Divergence for Normalizing Flows

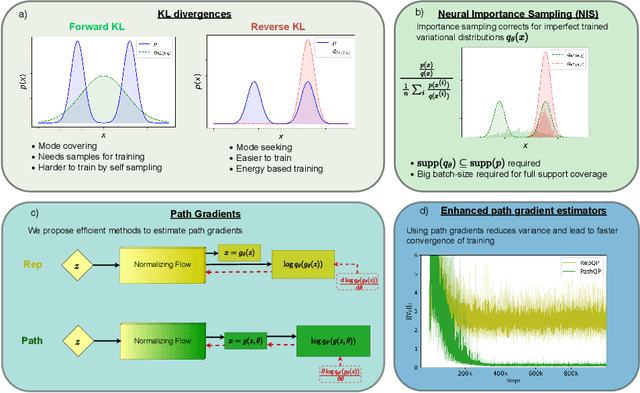
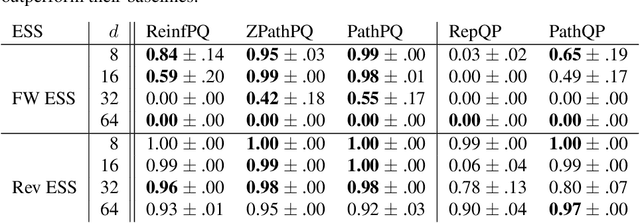
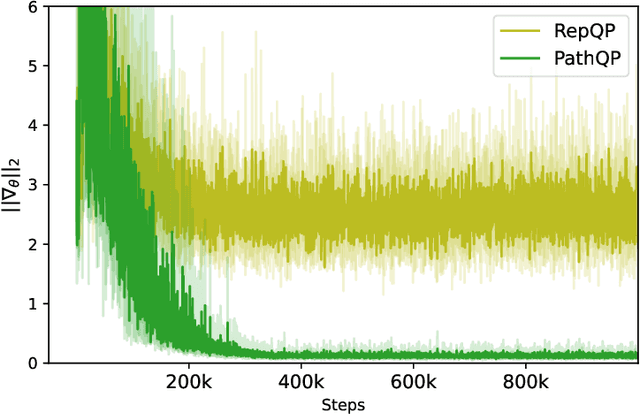
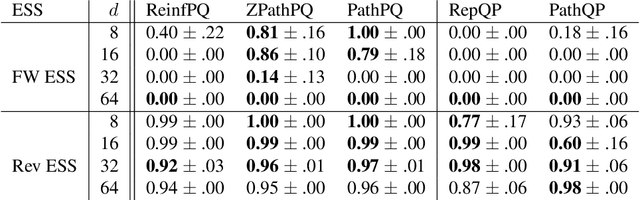
We propose an algorithm to estimate the path-gradient of both the reverse and forward Kullback-Leibler divergence for an arbitrary manifestly invertible normalizing flow. The resulting path-gradient estimators are straightforward to implement, have lower variance, and lead not only to faster convergence of training but also to better overall approximation results compared to standard total gradient estimators. We also demonstrate that path-gradient training is less susceptible to mode-collapse. In light of our results, we expect that path-gradient estimators will become the new standard method to train normalizing flows for variational inference.

Path-Gradient Estimators for Continuous Normalizing Flows

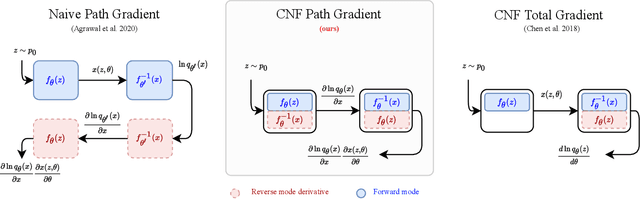
Recent work has established a path-gradient estimator for simple variational Gaussian distributions and has argued that the path-gradient is particularly beneficial in the regime in which the variational distribution approaches the exact target distribution. In many applications, this regime can however not be reached by a simple Gaussian variational distribution. In this work, we overcome this crucial limitation by proposing a path-gradient estimator for the considerably more expressive variational family of continuous normalizing flows. We outline an efficient algorithm to calculate this estimator and establish its superior performance empirically.

Diffeomorphic Counterfactuals with Generative Models

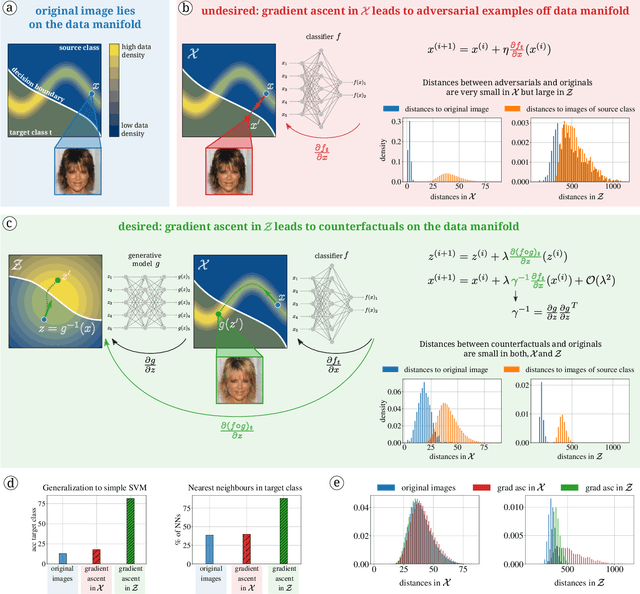
Counterfactuals can explain classification decisions of neural networks in a human interpretable way. We propose a simple but effective method to generate such counterfactuals. More specifically, we perform a suitable diffeomorphic coordinate transformation and then perform gradient ascent in these coordinates to find counterfactuals which are classified with great confidence as a specified target class. We propose two methods to leverage generative models to construct such suitable coordinate systems that are either exactly or approximately diffeomorphic. We analyze the generation process theoretically using Riemannian differential geometry and validate the quality of the generated counterfactuals using various qualitative and quantitative measures.

Machine Learning of Thermodynamic Observables in the Presence of Mode Collapse

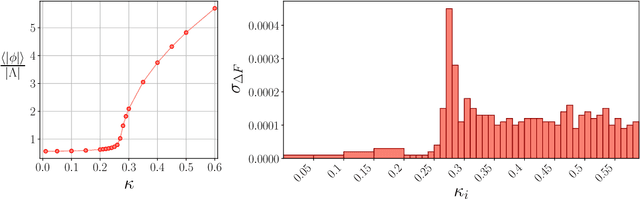
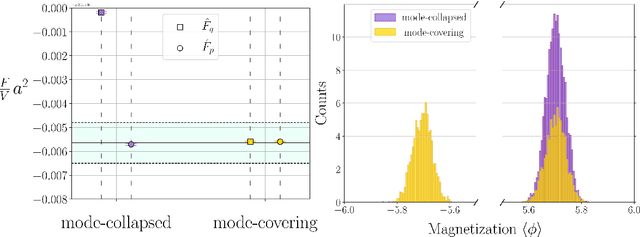
Estimating the free energy, as well as other thermodynamic observables, is a key task in lattice field theories. Recently, it has been pointed out that deep generative models can be used in this context [1]. Crucially, these models allow for the direct estimation of the free energy at a given point in parameter space. This is in contrast to existing methods based on Markov chains which generically require integration through parameter space. In this contribution, we will review this novel machine-learning-based estimation method. We will in detail discuss the issue of mode collapse and outline mitigation techniques which are particularly suited for applications at finite temperature.