Multilevel Generative Samplers for Investigating Critical Phenomena

Investigating critical phenomena or phase transitions is of high interest in physics and chemistry, for which Monte Carlo (MC) simulations, a crucial tool for numerically analyzing macroscopic properties of given systems, are often hindered by an emerging divergence of correlation length -- known as scale invariance at criticality (SIC) in the renormalization group theory. SIC causes the system to behave the same at any length scale, from which many existing sampling methods suffer: long-range correlations cause critical slowing down in Markov chain Monte Carlo (MCMC), and require intractably large receptive fields for generative samplers. In this paper, we propose a Renormalization-informed Generative Critical Sampler (RiGCS) -- a novel sampler specialized for near-critical systems, where SIC is leveraged as an advantage rather than a nuisance. Specifically, RiGCS builds on MultiLevel Monte Carlo (MLMC) with Heat Bath (HB) algorithms, which perform ancestral sampling from low-resolution to high-resolution lattice configurations with site-wise-independent conditional HB sampling. Although MLMC-HB is highly efficient under exact SIC, it suffers from a low acceptance rate under slight SIC violation. Notably, SIC violation always occurs in finite-size systems, and may induce long-range and higher-order interactions in the renormalized distributions, which are not considered by independent HB samplers. RiGCS enhances MLMC-HB by replacing a part of the conditional HB sampler with generative models that capture those residual interactions and improve the sampling efficiency. Our experiments show that the effective sample size of RiGCS is a few orders of magnitude higher than state-of-the-art generative model baselines in sampling configurations for 128x128 two-dimensional Ising systems.

Expressive equivalence of classical and quantum restricted Boltzmann machines

Quantum computers offer the potential for efficiently sampling from complex probability distributions, attracting increasing interest in generative modeling within quantum machine learning. This surge in interest has driven the development of numerous generative quantum models, yet their trainability and scalability remain significant challenges. A notable example is a quantum restricted Boltzmann machine (QRBM), which is based on the Gibbs state of a parameterized non-commuting Hamiltonian. While QRBMs are expressive, their non-commuting Hamiltonians make gradient evaluation computationally demanding, even on fault-tolerant quantum computers. In this work, we propose a semi-quantum restricted Boltzmann machine (sqRBM), a model designed for classical data that mitigates the challenges associated with previous QRBM proposals. The sqRBM Hamiltonian is commuting in the visible subspace while remaining non-commuting in the hidden subspace. This structure allows us to derive closed-form expressions for both output probabilities and gradients. Leveraging these analytical results, we demonstrate that sqRBMs share a close relationship with classical restricted Boltzmann machines (RBM). Our theoretical analysis predicts that, to learn a given probability distribution, an RBM requires three times as many hidden units as an sqRBM, while both models have the same total number of parameters. We validate these findings through numerical simulations involving up to 100 units. Our results suggest that sqRBMs could enable practical quantum machine learning applications in the near future by significantly reducing quantum resource requirements.

Bayesian Parameter Shift Rule in Variational Quantum Eigensolvers

Parameter shift rules (PSRs) are key techniques for efficient gradient estimation in variational quantum eigensolvers (VQEs). In this paper, we propose its Bayesian variant, where Gaussian processes with appropriate kernels are used to estimate the gradient of the VQE objective. Our Bayesian PSR offers flexible gradient estimation from observations at arbitrary locations with uncertainty information and reduces to the generalized PSR in special cases. In stochastic gradient descent (SGD), the flexibility of Bayesian PSR allows the reuse of observations in previous steps, which accelerates the optimization process. Furthermore, the accessibility to the posterior uncertainty, along with our proposed notion of gradient confident region (GradCoRe), enables us to minimize the observation costs in each SGD step. Our numerical experiments show that the VQE optimization with Bayesian PSR and GradCoRe significantly accelerates SGD and outperforms the state-of-the-art methods, including sequential minimal optimization.

Adaptive Observation Cost Control for Variational Quantum Eigensolvers

The objective to be minimized in the variational quantum eigensolver (VQE) has a restricted form, which allows a specialized sequential minimal optimization (SMO) that requires only a few observations in each iteration. However, the SMO iteration is still costly due to the observation noise -- one observation at a point typically requires averaging over hundreds to thousands of repeated quantum measurement shots for achieving a reasonable noise level. In this paper, we propose an adaptive cost control method, named subspace in confident region (SubsCoRe), for SMO. SubsCoRe uses the Gaussian process (GP) surrogate, and requires it to have low uncertainty over the subspace being updated, so that optimization in each iteration is performed with guaranteed accuracy. The adaptive cost control is performed by first setting the required accuracy according to the progress of the optimization, and then choosing the minimum number of measurement shots and their distribution such that the required accuracy is satisfied. We demonstrate that SubsCoRe significantly improves the efficiency of SMO, and outperforms the state-of-the-art methods.

Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects

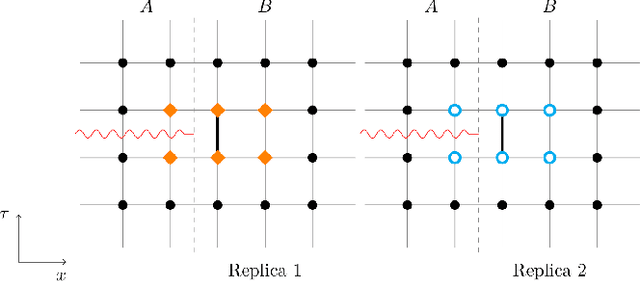
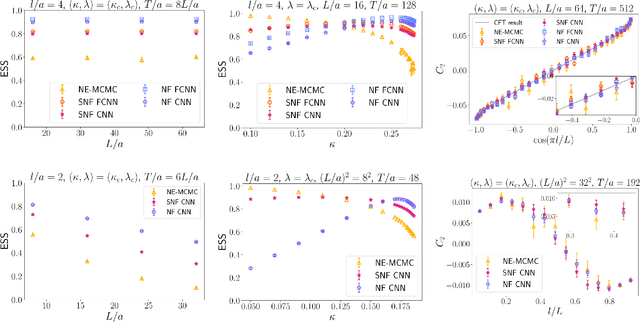
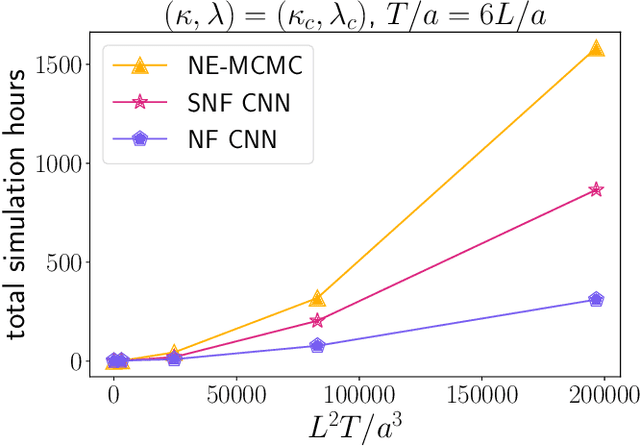
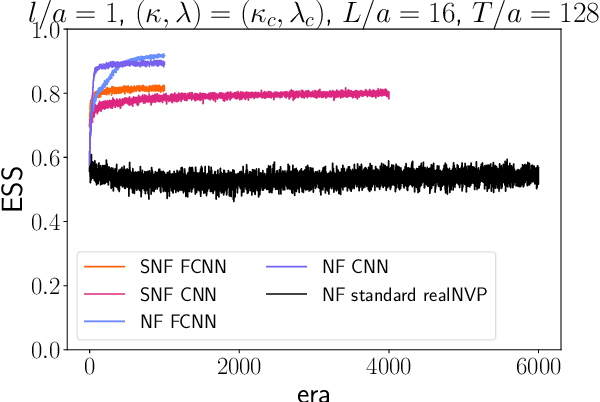
We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.

Developing a Framework for Sonifying Variational Quantum Algorithms: Implications for Music Composition

This chapter examines the Variational Quantum Harmonizer, a software tool and musical interface that focuses on the problem of sonification of the minimization steps of Variational Quantum Algorithms (VQA), used for simulating properties of quantum systems and optimization problems assisted by quantum hardware. Particularly, it details the sonification of Quadratic Unconstrained Binary Optimization (QUBO) problems using VQA. A flexible design enables its future applications both as a sonification tool for auditory displays in scientific investigation, and as a hybrid quantum-digital musical instrument for artistic endeavours. In turn, sonification can help researchers understand complex systems better and can serve for the training of quantum physics and quantum computing. The VQH structure, including its software implementation, control mechanisms, and sonification mappings are detailed. Moreover, it guides the design of QUBO cost functions in VQH as a music compositional object. The discussion is extended to the implications of applying quantum-assisted simulation in quantum-computer aided composition and live-coding performances. An artistic output is showcased by the piece \textit{Hexagonal Chambers} (Thomas and Itabora\'i, 2023).

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.

Symmetry breaking in geometric quantum machine learning in the presence of noise

Geometric quantum machine learning based on equivariant quantum neural networks (EQNN) recently appeared as a promising direction in quantum machine learning. Despite the encouraging progress, the studies are still limited to theory, and the role of hardware noise in EQNN training has never been explored. This work studies the behavior of EQNN models in the presence of noise. We show that certain EQNN models can preserve equivariance under Pauli channels, while this is not possible under the amplitude damping channel. We claim that the symmetry breaking grows linearly in the number of layers and noise strength. We support our claims with numerical data from simulations as well as hardware up to 64 qubits. Furthermore, we provide strategies to enhance the symmetry protection of EQNN models in the presence of noise.

Variational Quantum Harmonizer: Generating Chord Progressions and Other Sonification Methods with the VQE Algorithm

This work investigates a case study of using physical-based sonification of Quadratic Unconstrained Binary Optimization (QUBO) problems, optimized by the Variational Quantum Eigensolver (VQE) algorithm. The VQE approximates the solution of the problem by using an iterative loop between the quantum computer and a classical optimization routine. This work explores the intermediary statevectors found in each VQE iteration as the means of sonifying the optimization process itself. The implementation was realised in the form of a musical interface prototype named Variational Quantum Harmonizer (VQH), providing potential design strategies for musical applications, focusing on chords, chord progressions, and arpeggios. The VQH can be used both to enhance data visualization or to create artistic pieces. The methodology is also relevant in terms of how an artist would gain intuition towards achieving a desired musical sound by carefully designing QUBO cost functions. Flexible mapping strategies could supply a broad portfolio of sounds for QUBO and quantum-inspired musical compositions, as demonstrated in a case study composition, "Dependent Origination" by Peter Thomas and Paulo Itaborai.

Detecting and Mitigating Mode-Collapse for Flow-based Sampling of Lattice Field Theories

We study the consequences of mode-collapse of normalizing flows in the context of lattice field theory. Normalizing flows allow for independent sampling. For this reason, it is hoped that they can avoid the tunneling problem of local-update MCMC algorithms for multi-modal distributions. In this work, we first point out that the tunneling problem is also present for normalizing flows but is shifted from the sampling to the training phase of the algorithm. Specifically, normalizing flows often suffer from mode-collapse for which the training process assigns vanishingly low probability mass to relevant modes of the physical distribution. This may result in a significant bias when the flow is used as a sampler in a Markov-Chain or with Importance Sampling. We propose a metric to quantify the degree of mode-collapse and derive a bound on the resulting bias. Furthermore, we propose various mitigation strategies in particular in the context of estimating thermodynamic observables, such as the free energy.