A scalable flow-based approach to mitigate topological freezing

As lattice gauge theories with non-trivial topological features are driven towards the continuum limit, standard Markov Chain Monte Carlo simulations suffer for topological freezing, i.e., a dramatic growth of autocorrelations in topological observables. A widely used strategy is the adoption of Open Boundary Conditions (OBC), which restores ergodic sampling of topology but at the price of breaking translation invariance and introducing unphysical boundary artifacts. In this contribution we summarize a scalable, exact flow-based strategy to remove them by transporting configurations from a prior with a OBC defect to a fully periodic ensemble, and apply it to 4d SU(3) Yang--Mills theory. The method is based on a Stochastic Normalizing Flow (SNF) that alternates non-equilibrium Monte Carlo updates with localized, gauge-equivariant defect coupling layers implemented via masked parametric stout smearing. Training is performed by minimizing the average dissipated work, equivalent to a Kullback--Leibler divergence between forward and reverse non-equilibrium path measures, to achieve more reversible trajectories and improved efficiency. We discuss the scaling with the number of degrees of freedom affected by the defect and show that defect SNFs achieve better performances than purely stochastic non-equilibrium methods at comparable cost. Finally, we validate the approach by reproducing reference results for the topological susceptibility.

Toward Scalable Normalizing Flows for the Hubbard Model

Normalizing flows have recently demonstrated the ability to learn the Boltzmann distribution of the Hubbard model, opening new avenues for generative modeling in condensed matter physics. In this work, we investigate the steps required to extend such simulations to larger lattice sizes and lower temperatures, with a focus on enhancing stability and efficiency. Additionally, we present the scaling behavior of stochastic normalizing flows and non-equilibrium Markov chain Monte Carlo methods for this fermionic system.

Scaling flow-based approaches for topology sampling in $\mathrm{SU}(3)$ gauge theory

We develop a methodology based on out-of-equilibrium simulations to mitigate topological freezing when approaching the continuum limit of lattice gauge theories. We reduce the autocorrelation of the topological charge employing open boundary conditions, while removing exactly their unphysical effects using a non-equilibrium Monte Carlo approach in which periodic boundary conditions are gradually switched on. We perform a detailed analysis of the computational costs of this strategy in the case of the four-dimensional $\mathrm{SU}(3)$ Yang-Mills theory. After achieving full control of the scaling, we outline a clear strategy to sample topology efficiently in the continuum limit, which we check at lattice spacings as small as $0.045$ fm. We also generalize this approach by designing a customized Stochastic Normalizing Flow for evolutions in the boundary conditions, obtaining superior performances with respect to the purely stochastic non-equilibrium approach, and paving the way for more efficient future flow-based solutions.

Benchmarking Quantum Convolutional Neural Networks for Signal Classification in Simulated Gamma-Ray Burst Detection

This study evaluates the use of Quantum Convolutional Neural Networks (QCNNs) for identifying signals resembling Gamma-Ray Bursts (GRBs) within simulated astrophysical datasets in the form of light curves. The task addressed here focuses on distinguishing GRB-like signals from background noise in simulated Cherenkov Telescope Array Observatory (CTAO) data, the next-generation astrophysical observatory for very high-energy gamma-ray science. QCNNs, a quantum counterpart of classical Convolutional Neural Networks (CNNs), leverage quantum principles to process and analyze high-dimensional data efficiently. We implemented a hybrid quantum-classical machine learning technique using the Qiskit framework, with the QCNNs trained on a quantum simulator. Several QCNN architectures were tested, employing different encoding methods such as Data Reuploading and Amplitude encoding. Key findings include that QCNNs achieved accuracy comparable to classical CNNs, often surpassing 90\%, while using fewer parameters, potentially leading to more efficient models in terms of computational resources. A benchmark study further examined how hyperparameters like the number of qubits and encoding methods affected performance, with more qubits and advanced encoding methods generally enhancing accuracy but increasing complexity. QCNNs showed robust performance on time-series datasets, successfully detecting GRB signals with high precision. The research is a pioneering effort in applying QCNNs to astrophysics, offering insights into their potential and limitations. This work sets the stage for future investigations to fully realize the advantages of QCNNs in astrophysical data analysis.

Scaling of Stochastic Normalizing Flows in $\mathrm{SU}(3)$ lattice gauge theory

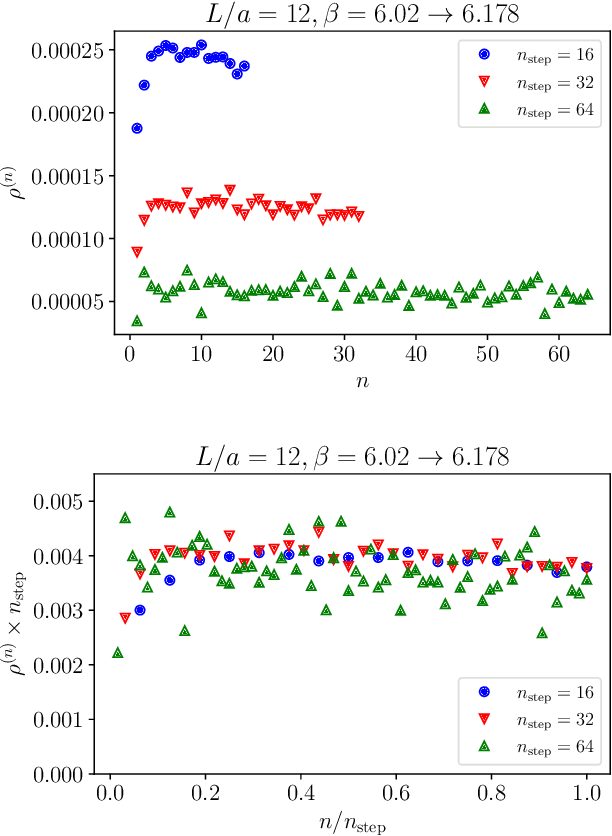
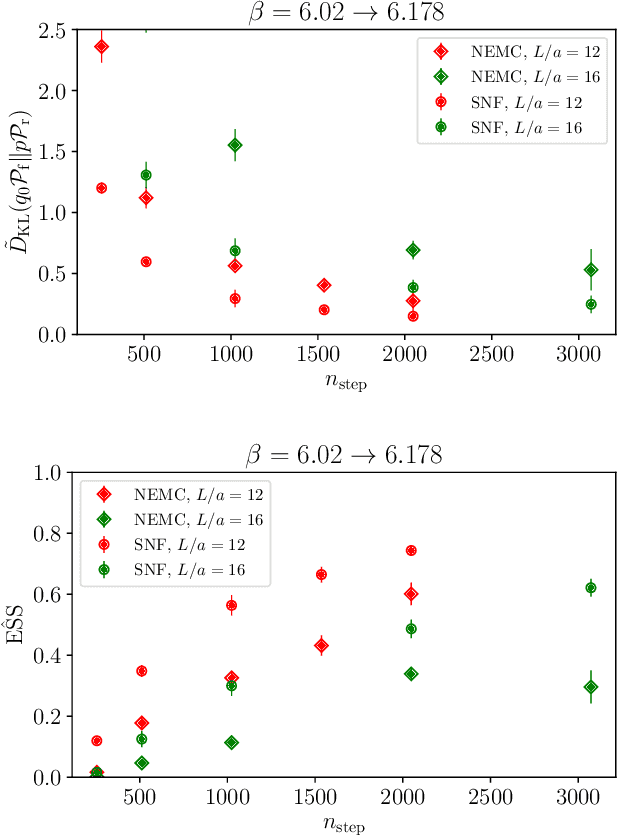
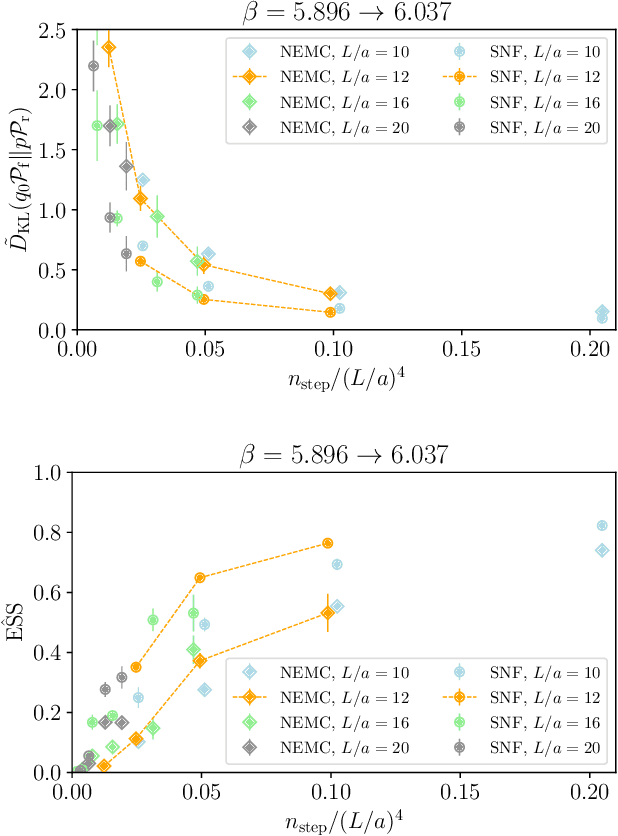
Non-equilibrium Markov Chain Monte Carlo (NE-MCMC) simulations provide a well-understood framework based on Jarzynski's equality to sample from a target probability distribution. By driving a base probability distribution out of equilibrium, observables are computed without the need to thermalize. If the base distribution is characterized by mild autocorrelations, this approach provides a way to mitigate critical slowing down. Out-of-equilibrium evolutions share the same framework of flow-based approaches and they can be naturally combined into a novel architecture called Stochastic Normalizing Flows (SNFs). In this work we present the first implementation of SNFs for $\mathrm{SU}(3)$ lattice gauge theory in 4 dimensions, defined by introducing gauge-equivariant layers between out-of-equilibrium Monte Carlo updates. The core of our analysis is focused on the promising scaling properties of this architecture with the degrees of freedom of the system, which are directly inherited from NE-MCMC. Finally, we discuss how systematic improvements of this approach can realistically lead to a general and yet efficient sampling strategy at fine lattice spacings for observables affected by long autocorrelation times.

Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects

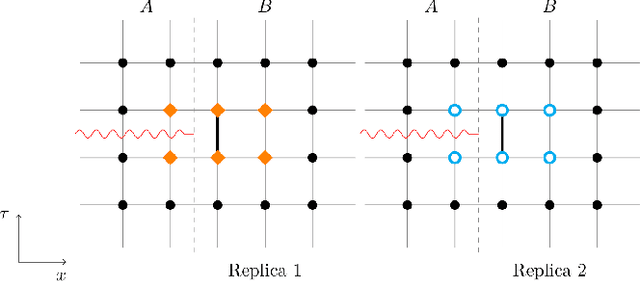
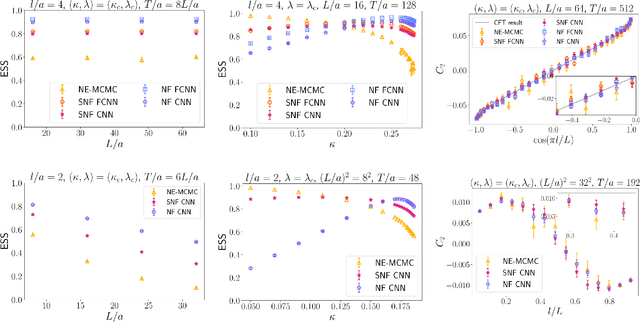
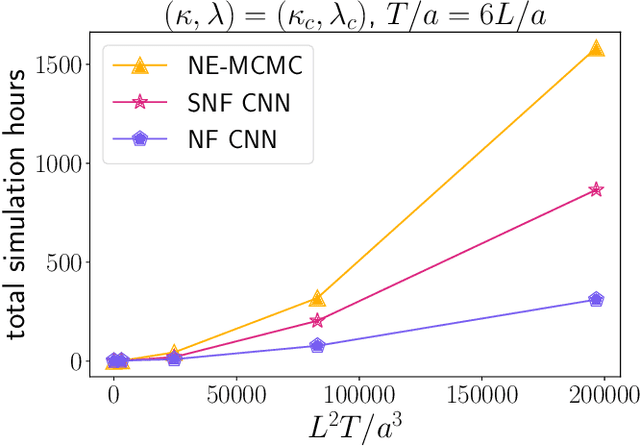
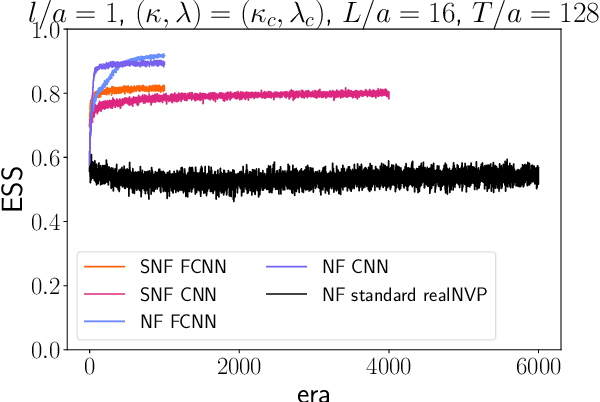
We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.