Scaling of Stochastic Normalizing Flows in $\mathrm{SU}(3)$ lattice gauge theory
Paper and Code
Nov 29, 2024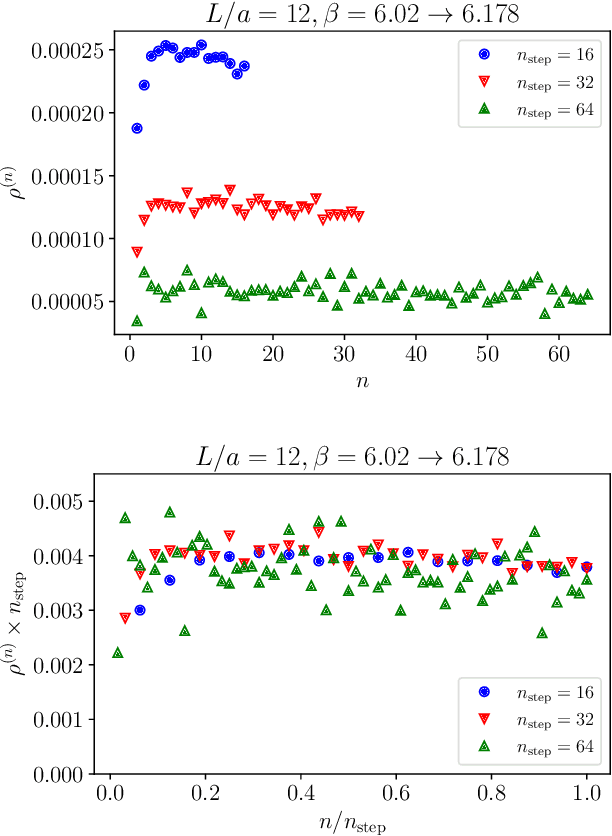
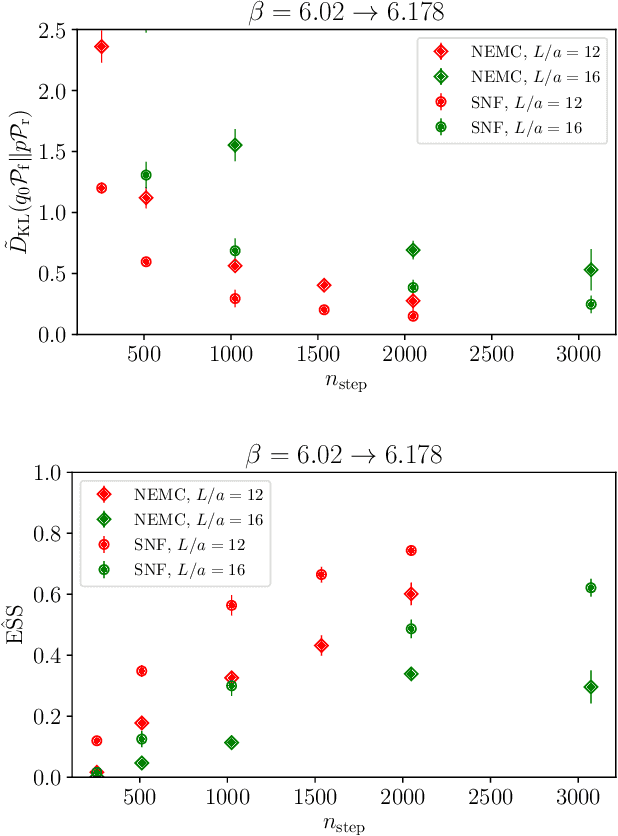
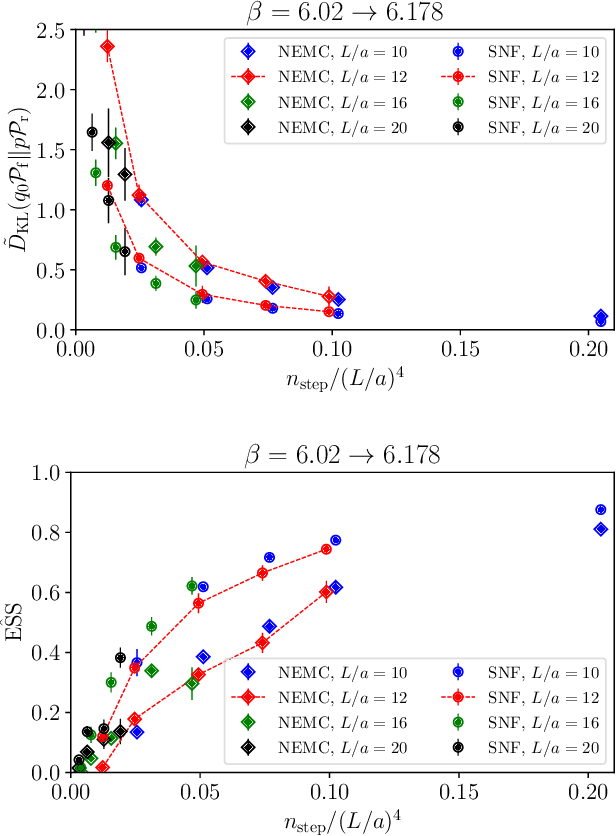
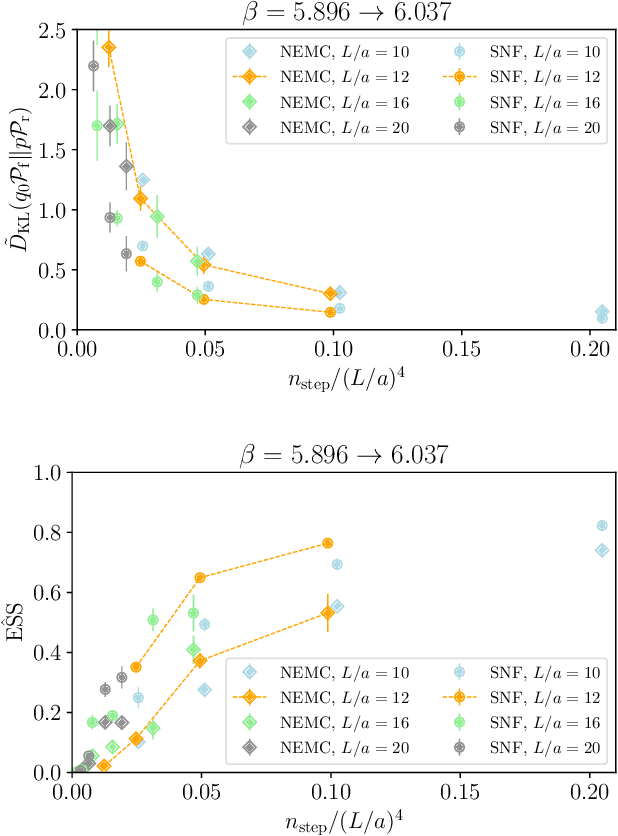
Non-equilibrium Markov Chain Monte Carlo (NE-MCMC) simulations provide a well-understood framework based on Jarzynski's equality to sample from a target probability distribution. By driving a base probability distribution out of equilibrium, observables are computed without the need to thermalize. If the base distribution is characterized by mild autocorrelations, this approach provides a way to mitigate critical slowing down. Out-of-equilibrium evolutions share the same framework of flow-based approaches and they can be naturally combined into a novel architecture called Stochastic Normalizing Flows (SNFs). In this work we present the first implementation of SNFs for $\mathrm{SU}(3)$ lattice gauge theory in 4 dimensions, defined by introducing gauge-equivariant layers between out-of-equilibrium Monte Carlo updates. The core of our analysis is focused on the promising scaling properties of this architecture with the degrees of freedom of the system, which are directly inherited from NE-MCMC. Finally, we discuss how systematic improvements of this approach can realistically lead to a general and yet efficient sampling strategy at fine lattice spacings for observables affected by long autocorrelation times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge