Scaling of Stochastic Normalizing Flows in $\mathrm{SU}(3)$ lattice gauge theory

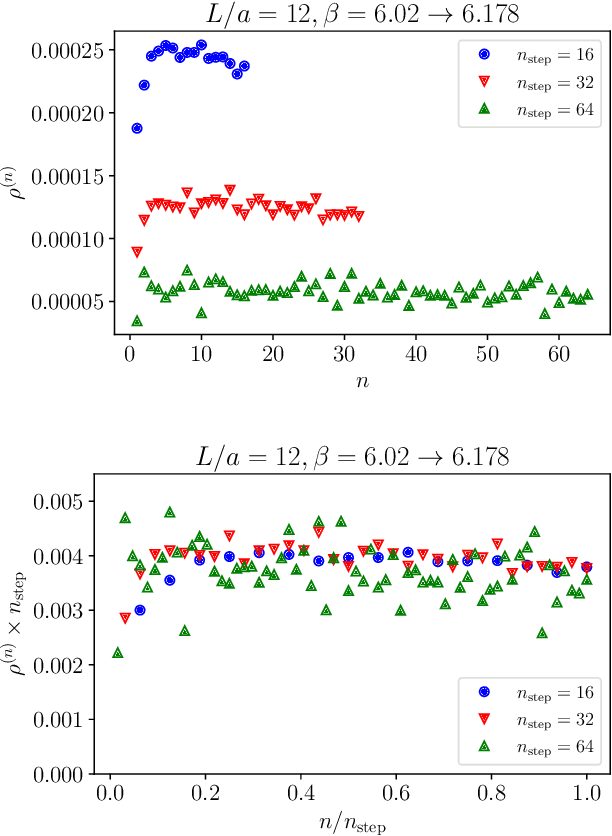
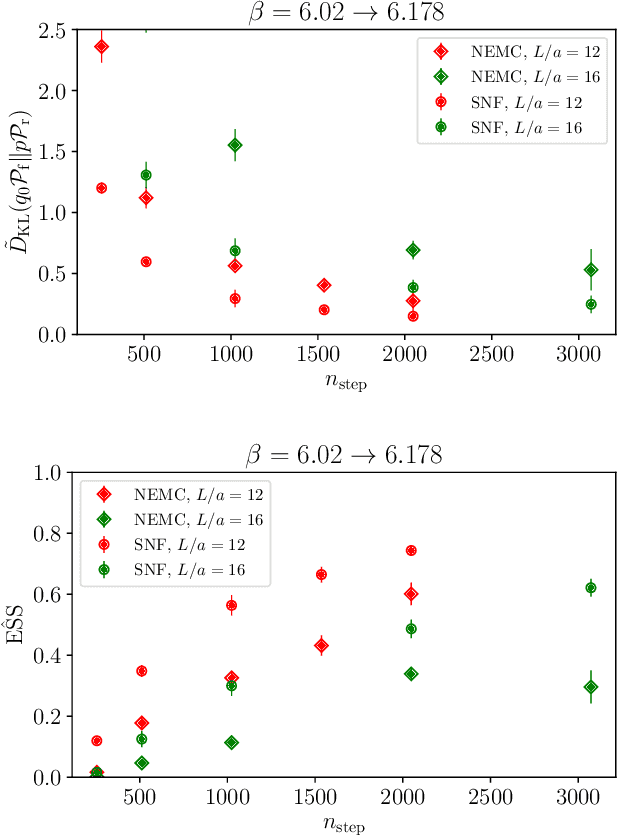
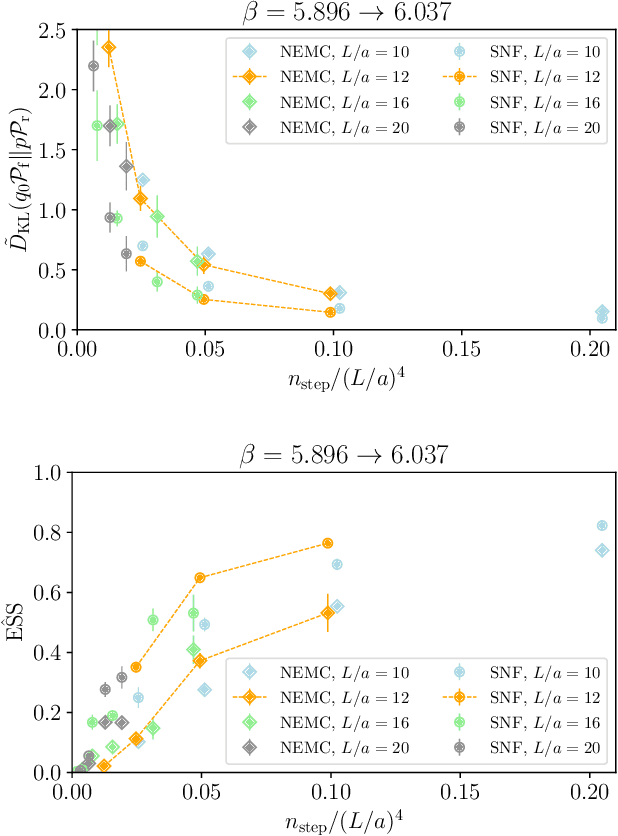
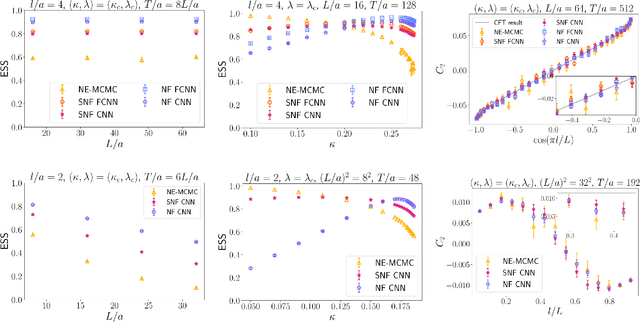
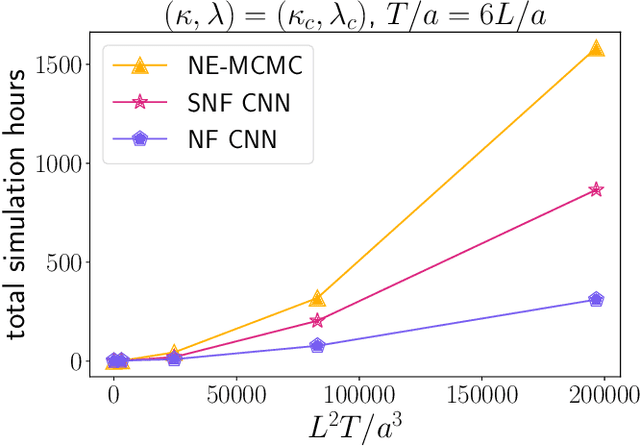
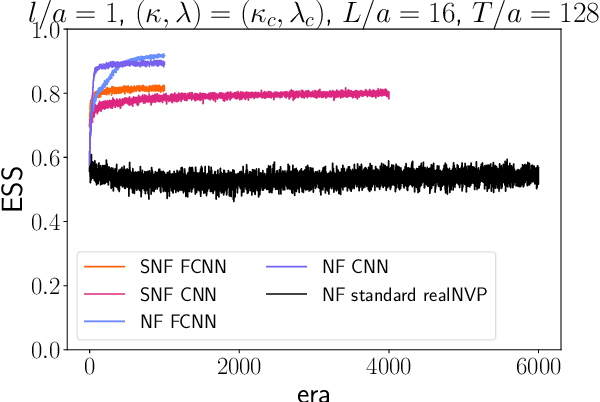
Non-equilibrium Markov Chain Monte Carlo (NE-MCMC) simulations provide a well-understood framework based on Jarzynski's equality to sample from a target probability distribution. By driving a base probability distribution out of equilibrium, observables are computed without the need to thermalize. If the base distribution is characterized by mild autocorrelations, this approach provides a way to mitigate critical slowing down. Out-of-equilibrium evolutions share the same framework of flow-based approaches and they can be naturally combined into a novel architecture called Stochastic Normalizing Flows (SNFs). In this work we present the first implementation of SNFs for $\mathrm{SU}(3)$ lattice gauge theory in 4 dimensions, defined by introducing gauge-equivariant layers between out-of-equilibrium Monte Carlo updates. The core of our analysis is focused on the promising scaling properties of this architecture with the degrees of freedom of the system, which are directly inherited from NE-MCMC. Finally, we discuss how systematic improvements of this approach can realistically lead to a general and yet efficient sampling strategy at fine lattice spacings for observables affected by long autocorrelation times.

Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects

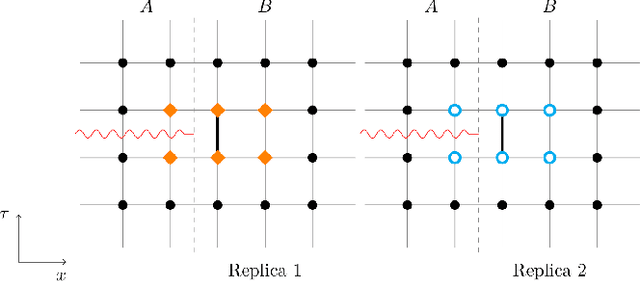
We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.

Numerical determination of the width and shape of the effective string using Stochastic Normalizing Flows

Flow-based architectures have recently proved to be an efficient tool for numerical simulations of Effective String Theories regularized on the lattice that otherwise cannot be efficiently sampled by standard Monte Carlo methods. In this work we use Stochastic Normalizing Flows, a state-of-the-art deep-learning architecture based on non-equilibrium Monte Carlo simulations, to study different effective string models. After testing the reliability of this approach through a comparison with exact results for the Nambu-Got\={o} model, we discuss results on observables that are challenging to study analytically, such as the width of the string and the shape of the flux density. Furthermore, we perform a novel numerical study of Effective String Theories with terms beyond the Nambu-Got\={o} action, including a broader discussion on their significance for lattice gauge theories. These results establish the reliability and feasibility of flow-based samplers for Effective String Theories and pave the way for future applications on more complex models.

Sampling the lattice Nambu-Goto string using Continuous Normalizing Flows

Effective String Theory (EST) represents a powerful non-perturbative approach to describe confinement in Yang-Mills theory that models the confining flux tube as a thin vibrating string. EST calculations are usually performed using the zeta-function regularization: however there are situations (for instance the study of the shape of the flux tube or of the higher order corrections beyond the Nambu-Goto EST) which involve observables that are too complex to be addressed in this way. In this paper we propose a numerical approach based on recent advances in machine learning methods to circumvent this problem. Using as a laboratory the Nambu-Goto string, we show that by using a new class of deep generative models called Continuous Normalizing Flows it is possible to obtain reliable numerical estimates of EST predictions.

Stochastic normalizing flows as non-equilibrium transformations

Normalizing flows are a class of deep generative models that provide a promising route to sample lattice field theories more efficiently than conventional Monte~Carlo simulations. In this work we show that the theoretical framework of stochastic normalizing flows, in which neural-network layers are combined with Monte~Carlo updates, is the same that underlies out-of-equilibrium simulations based on Jarzynski's equality, which have been recently deployed to compute free-energy differences in lattice gauge theories. We lay out a strategy to optimize the efficiency of this extended class of generative models and present examples of applications.