Multilevel Generative Samplers for Investigating Critical Phenomena

Investigating critical phenomena or phase transitions is of high interest in physics and chemistry, for which Monte Carlo (MC) simulations, a crucial tool for numerically analyzing macroscopic properties of given systems, are often hindered by an emerging divergence of correlation length -- known as scale invariance at criticality (SIC) in the renormalization group theory. SIC causes the system to behave the same at any length scale, from which many existing sampling methods suffer: long-range correlations cause critical slowing down in Markov chain Monte Carlo (MCMC), and require intractably large receptive fields for generative samplers. In this paper, we propose a Renormalization-informed Generative Critical Sampler (RiGCS) -- a novel sampler specialized for near-critical systems, where SIC is leveraged as an advantage rather than a nuisance. Specifically, RiGCS builds on MultiLevel Monte Carlo (MLMC) with Heat Bath (HB) algorithms, which perform ancestral sampling from low-resolution to high-resolution lattice configurations with site-wise-independent conditional HB sampling. Although MLMC-HB is highly efficient under exact SIC, it suffers from a low acceptance rate under slight SIC violation. Notably, SIC violation always occurs in finite-size systems, and may induce long-range and higher-order interactions in the renormalized distributions, which are not considered by independent HB samplers. RiGCS enhances MLMC-HB by replacing a part of the conditional HB sampler with generative models that capture those residual interactions and improve the sampling efficiency. Our experiments show that the effective sample size of RiGCS is a few orders of magnitude higher than state-of-the-art generative model baselines in sampling configurations for 128x128 two-dimensional Ising systems.

Adaptive Observation Cost Control for Variational Quantum Eigensolvers

The objective to be minimized in the variational quantum eigensolver (VQE) has a restricted form, which allows a specialized sequential minimal optimization (SMO) that requires only a few observations in each iteration. However, the SMO iteration is still costly due to the observation noise -- one observation at a point typically requires averaging over hundreds to thousands of repeated quantum measurement shots for achieving a reasonable noise level. In this paper, we propose an adaptive cost control method, named subspace in confident region (SubsCoRe), for SMO. SubsCoRe uses the Gaussian process (GP) surrogate, and requires it to have low uncertainty over the subspace being updated, so that optimization in each iteration is performed with guaranteed accuracy. The adaptive cost control is performed by first setting the required accuracy according to the progress of the optimization, and then choosing the minimum number of measurement shots and their distribution such that the required accuracy is satisfied. We demonstrate that SubsCoRe significantly improves the efficiency of SMO, and outperforms the state-of-the-art methods.

Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects

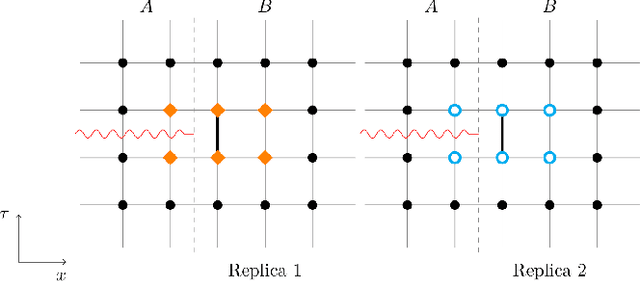
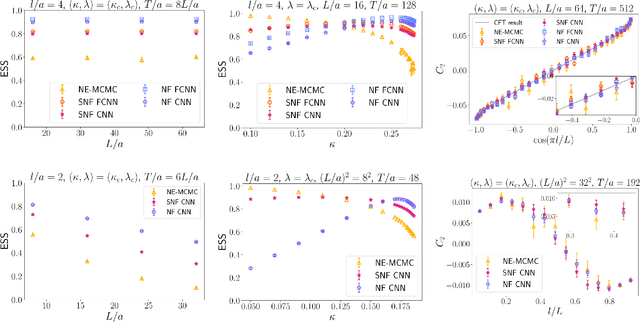
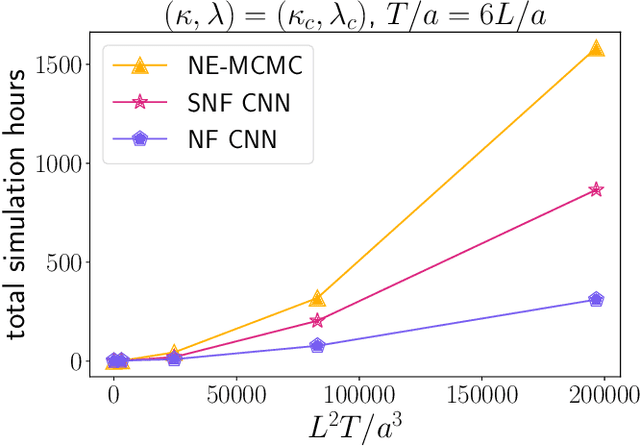
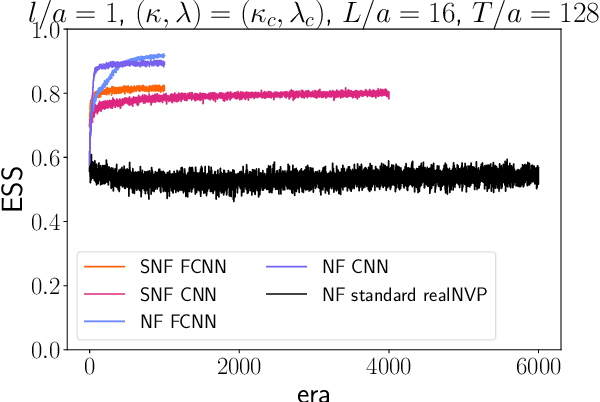
We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.