Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.

Detecting and Mitigating Mode-Collapse for Flow-based Sampling of Lattice Field Theories

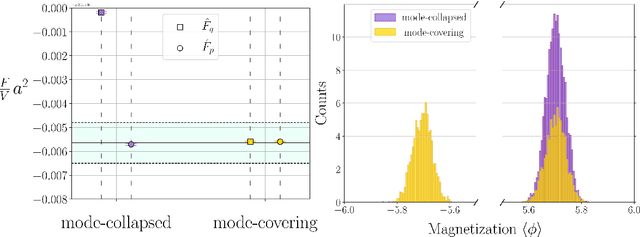
We study the consequences of mode-collapse of normalizing flows in the context of lattice field theory. Normalizing flows allow for independent sampling. For this reason, it is hoped that they can avoid the tunneling problem of local-update MCMC algorithms for multi-modal distributions. In this work, we first point out that the tunneling problem is also present for normalizing flows but is shifted from the sampling to the training phase of the algorithm. Specifically, normalizing flows often suffer from mode-collapse for which the training process assigns vanishingly low probability mass to relevant modes of the physical distribution. This may result in a significant bias when the flow is used as a sampler in a Markov-Chain or with Importance Sampling. We propose a metric to quantify the degree of mode-collapse and derive a bound on the resulting bias. Furthermore, we propose various mitigation strategies in particular in the context of estimating thermodynamic observables, such as the free energy.

Machine Learning of Thermodynamic Observables in the Presence of Mode Collapse

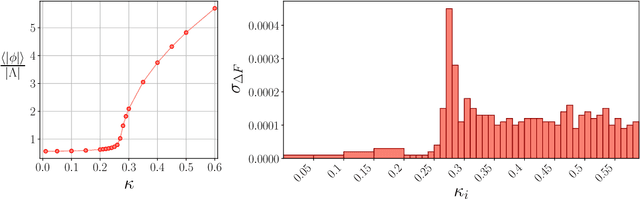
Estimating the free energy, as well as other thermodynamic observables, is a key task in lattice field theories. Recently, it has been pointed out that deep generative models can be used in this context [1]. Crucially, these models allow for the direct estimation of the free energy at a given point in parameter space. This is in contrast to existing methods based on Markov chains which generically require integration through parameter space. In this contribution, we will review this novel machine-learning-based estimation method. We will in detail discuss the issue of mode collapse and outline mitigation techniques which are particularly suited for applications at finite temperature.

On Estimation of Thermodynamic Observables in Lattice Field Theories with Deep Generative Models

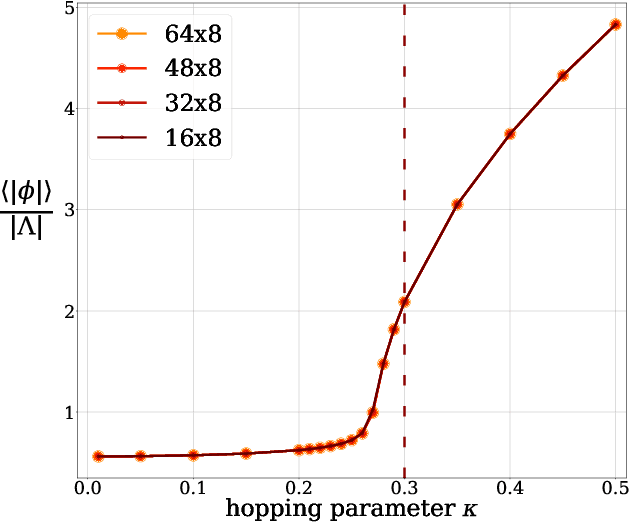
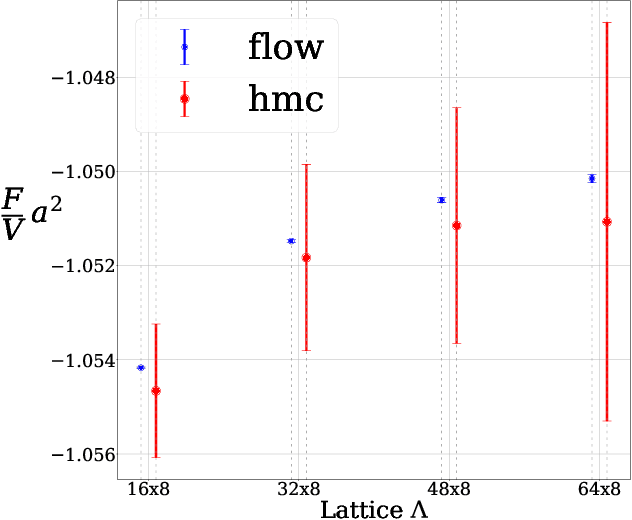
In this work, we demonstrate that applying deep generative machine learning models for lattice field theory is a promising route for solving problems where Markov Chain Monte Carlo (MCMC) methods are problematic. More specifically, we show that generative models can be used to estimate the absolute value of the free energy, which is in contrast to existing MCMC-based methods which are limited to only estimate free energy differences. We demonstrate the effectiveness of the proposed method for two-dimensional $\phi^4$ theory and compare it to MCMC-based methods in detailed numerical experiments.