Bayesian Parameter Shift Rule in Variational Quantum Eigensolvers

Parameter shift rules (PSRs) are key techniques for efficient gradient estimation in variational quantum eigensolvers (VQEs). In this paper, we propose its Bayesian variant, where Gaussian processes with appropriate kernels are used to estimate the gradient of the VQE objective. Our Bayesian PSR offers flexible gradient estimation from observations at arbitrary locations with uncertainty information and reduces to the generalized PSR in special cases. In stochastic gradient descent (SGD), the flexibility of Bayesian PSR allows the reuse of observations in previous steps, which accelerates the optimization process. Furthermore, the accessibility to the posterior uncertainty, along with our proposed notion of gradient confident region (GradCoRe), enables us to minimize the observation costs in each SGD step. Our numerical experiments show that the VQE optimization with Bayesian PSR and GradCoRe significantly accelerates SGD and outperforms the state-of-the-art methods, including sequential minimal optimization.

Adaptive Observation Cost Control for Variational Quantum Eigensolvers

The objective to be minimized in the variational quantum eigensolver (VQE) has a restricted form, which allows a specialized sequential minimal optimization (SMO) that requires only a few observations in each iteration. However, the SMO iteration is still costly due to the observation noise -- one observation at a point typically requires averaging over hundreds to thousands of repeated quantum measurement shots for achieving a reasonable noise level. In this paper, we propose an adaptive cost control method, named subspace in confident region (SubsCoRe), for SMO. SubsCoRe uses the Gaussian process (GP) surrogate, and requires it to have low uncertainty over the subspace being updated, so that optimization in each iteration is performed with guaranteed accuracy. The adaptive cost control is performed by first setting the required accuracy according to the progress of the optimization, and then choosing the minimum number of measurement shots and their distribution such that the required accuracy is satisfied. We demonstrate that SubsCoRe significantly improves the efficiency of SMO, and outperforms the state-of-the-art methods.

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.

Towards Fixing Clever-Hans Predictors with Counterfactual Knowledge Distillation

This paper introduces a novel technique called counterfactual knowledge distillation (CFKD) to detect and remove reliance on confounders in deep learning models with the help of human expert feedback. Confounders are spurious features that models tend to rely on, which can result in unexpected errors in regulated or safety-critical domains. The paper highlights the benefit of CFKD in such domains and shows some advantages of counterfactual explanations over other types of explanations. We propose an experiment scheme to quantitatively evaluate the success of CFKD and different teachers that can give feedback to the model. We also introduce a new metric that is better correlated with true test performance than validation accuracy. The paper demonstrates the effectiveness of CFKD on synthetically augmented datasets and on real-world histopathological datasets.

From Hope to Safety: Unlearning Biases of Deep Models by Enforcing the Right Reasons in Latent Space

Deep Neural Networks are prone to learning spurious correlations embedded in the training data, leading to potentially biased predictions. This poses risks when deploying these models for high-stake decision-making, such as in medical applications. Current methods for post-hoc model correction either require input-level annotations, which are only possible for spatially localized biases, or augment the latent feature space, thereby hoping to enforce the right reasons. We present a novel method ensuring the right reasons on the concept level by reducing the model's sensitivity towards biases through the gradient. When modeling biases via Concept Activation Vectors, we highlight the importance of choosing robust directions, as traditional regression-based approaches such as Support Vector Machines tend to result in diverging directions. We effectively mitigate biases in controlled and real-world settings on the ISIC, Bone Age, ImageNet and CelebA datasets using VGG, ResNet and EfficientNet architectures.

Detecting and Mitigating Mode-Collapse for Flow-based Sampling of Lattice Field Theories

We study the consequences of mode-collapse of normalizing flows in the context of lattice field theory. Normalizing flows allow for independent sampling. For this reason, it is hoped that they can avoid the tunneling problem of local-update MCMC algorithms for multi-modal distributions. In this work, we first point out that the tunneling problem is also present for normalizing flows but is shifted from the sampling to the training phase of the algorithm. Specifically, normalizing flows often suffer from mode-collapse for which the training process assigns vanishingly low probability mass to relevant modes of the physical distribution. This may result in a significant bias when the flow is used as a sampler in a Markov-Chain or with Importance Sampling. We propose a metric to quantify the degree of mode-collapse and derive a bound on the resulting bias. Furthermore, we propose various mitigation strategies in particular in the context of estimating thermodynamic observables, such as the free energy.

PatClArC: Using Pattern Concept Activation Vectors for Noise-Robust Model Debugging

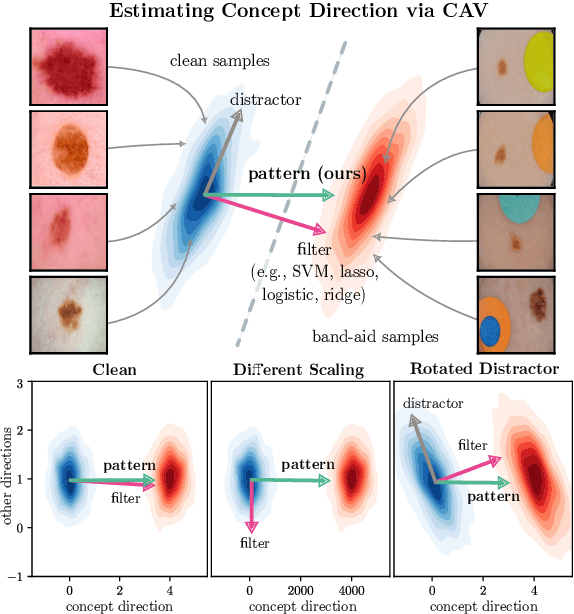
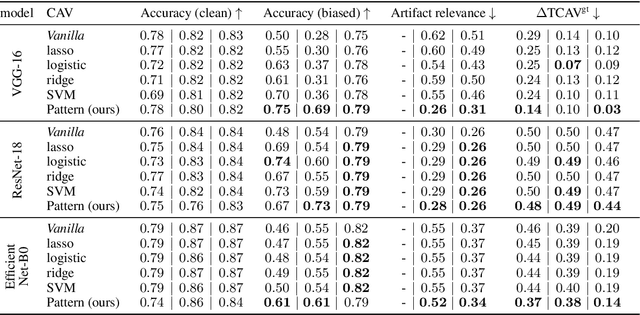
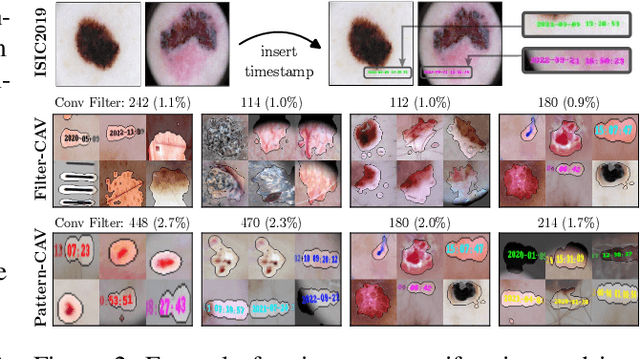
State-of-the-art machine learning models are commonly (pre-)trained on large benchmark datasets. These often contain biases, artifacts, or errors that have remained unnoticed in the data collection process and therefore fail in representing the real world truthfully. This can cause models trained on these datasets to learn undesired behavior based upon spurious correlations, e.g., the existence of a copyright tag in an image. Concept Activation Vectors (CAV) have been proposed as a tool to model known concepts in latent space and have been used for concept sensitivity testing and model correction. Specifically, class artifact compensation (ClArC) corrects models using CAVs to represent data artifacts in feature space linearly. Modeling CAVs with filters of linear models, however, causes a significant influence of the noise portion within the data, as recent work proposes the unsuitability of linear model filters to find the signal direction in the input, which can be avoided by instead using patterns. In this paper we propose Pattern Concept Activation Vectors (PCAV) for noise-robust concept representations in latent space. We demonstrate that pattern-based artifact modeling has beneficial effects on the application of CAVs as a means to remove influence of confounding features from models via the ClArC framework.

Software for Dataset-wide XAI: From Local Explanations to Global Insights with Zennit, CoRelAy, and ViRelAy

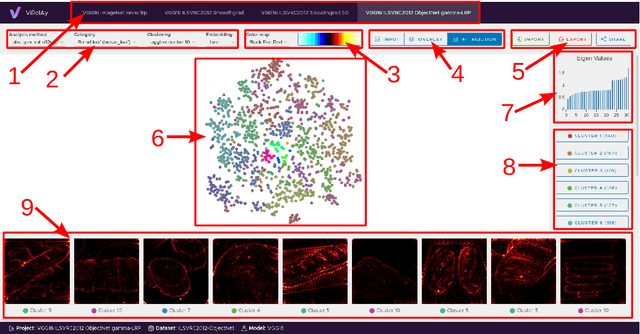
Deep Neural Networks (DNNs) are known to be strong predictors, but their prediction strategies can rarely be understood. With recent advances in Explainable Artificial Intelligence, approaches are available to explore the reasoning behind those complex models' predictions. One class of approaches are post-hoc attribution methods, among which Layer-wise Relevance Propagation (LRP) shows high performance. However, the attempt at understanding a DNN's reasoning often stops at the attributions obtained for individual samples in input space, leaving the potential for deeper quantitative analyses untouched. As a manual analysis without the right tools is often unnecessarily labor intensive, we introduce three software packages targeted at scientists to explore model reasoning using attribution approaches and beyond: (1) Zennit - a highly customizable and intuitive attribution framework implementing LRP and related approaches in PyTorch, (2) CoRelAy - a framework to easily and quickly construct quantitative analysis pipelines for dataset-wide analyses of explanations, and (3) ViRelAy - a web-application to interactively explore data, attributions, and analysis results.

Towards Robust Explanations for Deep Neural Networks

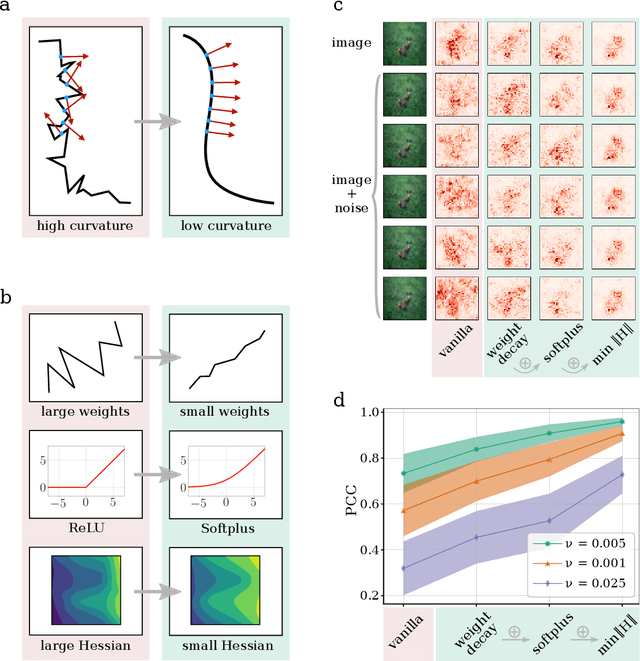
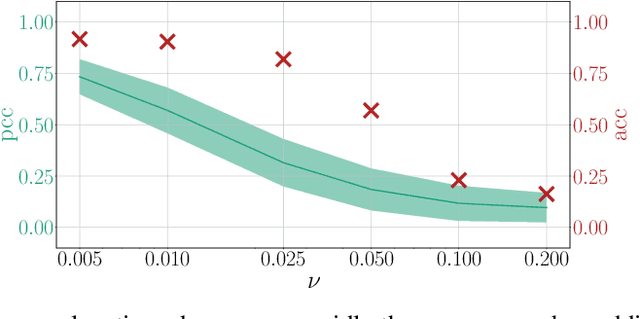
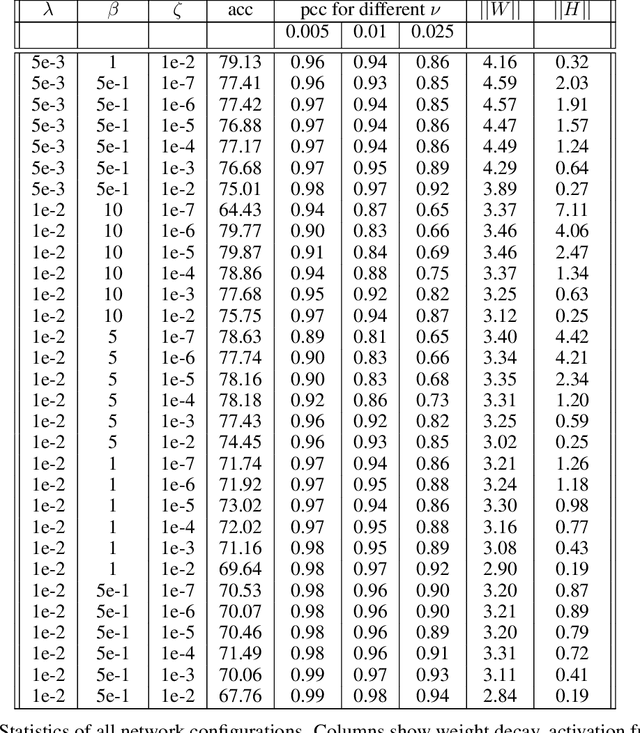
Explanation methods shed light on the decision process of black-box classifiers such as deep neural networks. But their usefulness can be compromised because they are susceptible to manipulations. With this work, we aim to enhance the resilience of explanations. We develop a unified theoretical framework for deriving bounds on the maximal manipulability of a model. Based on these theoretical insights, we present three different techniques to boost robustness against manipulation: training with weight decay, smoothing activation functions, and minimizing the Hessian of the network. Our experimental results confirm the effectiveness of these approaches.

Fairwashing Explanations with Off-Manifold Detergent

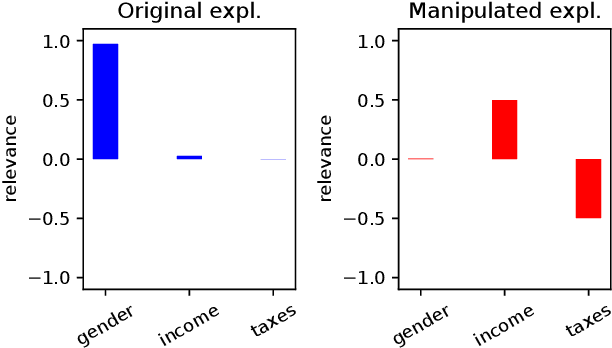
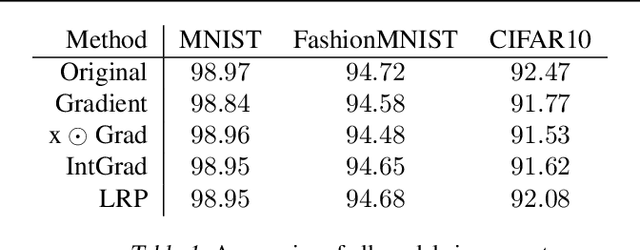
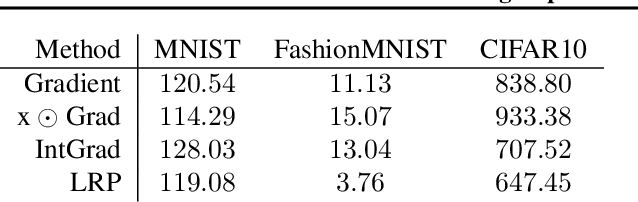
Explanation methods promise to make black-box classifiers more transparent. As a result, it is hoped that they can act as proof for a sensible, fair and trustworthy decision-making process of the algorithm and thereby increase its acceptance by the end-users. In this paper, we show both theoretically and experimentally that these hopes are presently unfounded. Specifically, we show that, for any classifier $g$, one can always construct another classifier $\tilde{g}$ which has the same behavior on the data (same train, validation, and test error) but has arbitrarily manipulated explanation maps. We derive this statement theoretically using differential geometry and demonstrate it experimentally for various explanation methods, architectures, and datasets. Motivated by our theoretical insights, we then propose a modification of existing explanation methods which makes them significantly more robust.