Bayesian Parameter Shift Rule in Variational Quantum Eigensolvers

Parameter shift rules (PSRs) are key techniques for efficient gradient estimation in variational quantum eigensolvers (VQEs). In this paper, we propose its Bayesian variant, where Gaussian processes with appropriate kernels are used to estimate the gradient of the VQE objective. Our Bayesian PSR offers flexible gradient estimation from observations at arbitrary locations with uncertainty information and reduces to the generalized PSR in special cases. In stochastic gradient descent (SGD), the flexibility of Bayesian PSR allows the reuse of observations in previous steps, which accelerates the optimization process. Furthermore, the accessibility to the posterior uncertainty, along with our proposed notion of gradient confident region (GradCoRe), enables us to minimize the observation costs in each SGD step. Our numerical experiments show that the VQE optimization with Bayesian PSR and GradCoRe significantly accelerates SGD and outperforms the state-of-the-art methods, including sequential minimal optimization.

Adaptive Observation Cost Control for Variational Quantum Eigensolvers

The objective to be minimized in the variational quantum eigensolver (VQE) has a restricted form, which allows a specialized sequential minimal optimization (SMO) that requires only a few observations in each iteration. However, the SMO iteration is still costly due to the observation noise -- one observation at a point typically requires averaging over hundreds to thousands of repeated quantum measurement shots for achieving a reasonable noise level. In this paper, we propose an adaptive cost control method, named subspace in confident region (SubsCoRe), for SMO. SubsCoRe uses the Gaussian process (GP) surrogate, and requires it to have low uncertainty over the subspace being updated, so that optimization in each iteration is performed with guaranteed accuracy. The adaptive cost control is performed by first setting the required accuracy according to the progress of the optimization, and then choosing the minimum number of measurement shots and their distribution such that the required accuracy is satisfied. We demonstrate that SubsCoRe significantly improves the efficiency of SMO, and outperforms the state-of-the-art methods.

Machine-Learning-Enhanced Optimization of Noise-Resilient Variational Quantum Eigensolvers

Variational Quantum Eigensolvers (VQEs) are a powerful class of hybrid quantum-classical algorithms designed to approximate the ground state of a quantum system described by its Hamiltonian. VQEs hold promise for various applications, including lattice field theory. However, the inherent noise of Noisy Intermediate-Scale Quantum (NISQ) devices poses a significant challenge for running VQEs as these algorithms are particularly susceptible to noise, e.g., measurement shot noise and hardware noise. In a recent work, it was proposed to enhance the classical optimization of VQEs with Gaussian Processes (GPs) and Bayesian Optimization, as these machine-learning techniques are well-suited for handling noisy data. In these proceedings, we provide additional insights into this new algorithm and present further numerical experiments. In particular, we examine the impact of hardware noise and error mitigation on the algorithm's performance. We validate the algorithm using classical simulations of quantum hardware, including hardware noise benchmarks, which have not been considered in previous works. Our numerical experiments demonstrate that GP-enhanced algorithms can outperform state-of-the-art baselines, laying the foundation for future research on deploying these techniques to real quantum hardware and lattice field theory setups.

Simulating the Hubbard Model with Equivariant Normalizing Flows

Generative models, particularly normalizing flows, have shown exceptional performance in learning probability distributions across various domains of physics, including statistical mechanics, collider physics, and lattice field theory. In the context of lattice field theory, normalizing flows have been successfully applied to accurately learn the Boltzmann distribution, enabling a range of tasks such as direct estimation of thermodynamic observables and sampling independent and identically distributed (i.i.d.) configurations. In this work, we present a proof-of-concept demonstration that normalizing flows can be used to learn the Boltzmann distribution for the Hubbard model. This model is widely employed to study the electronic structure of graphene and other carbon nanomaterials. State-of-the-art numerical simulations of the Hubbard model, such as those based on Hybrid Monte Carlo (HMC) methods, often suffer from ergodicity issues, potentially leading to biased estimates of physical observables. Our numerical experiments demonstrate that leveraging i.i.d.\ sampling from the normalizing flow effectively addresses these issues.

Flow-based Sampling for Entanglement Entropy and the Machine Learning of Defects

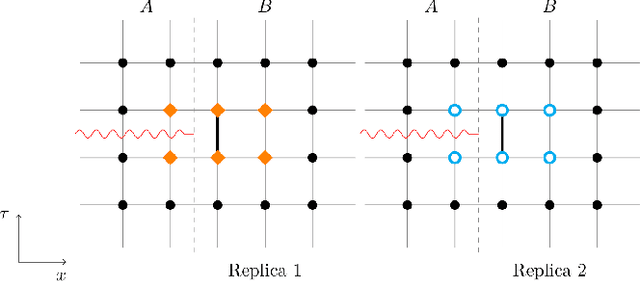
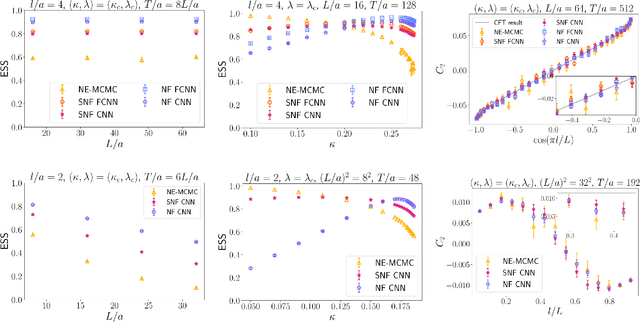
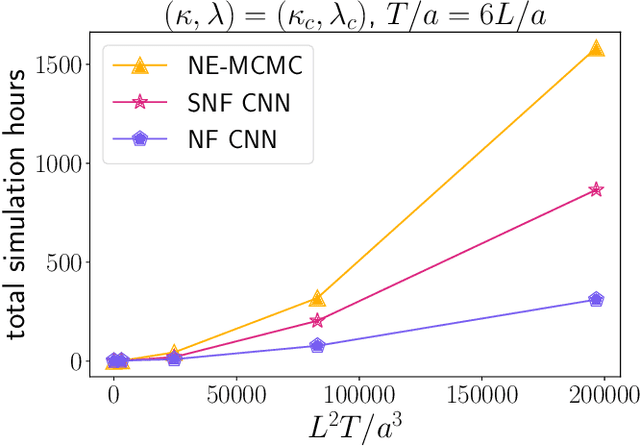
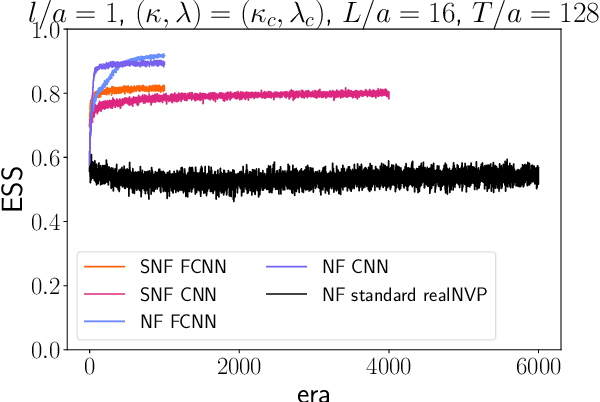
We introduce a novel technique to numerically calculate R\'enyi entanglement entropies in lattice quantum field theory using generative models. We describe how flow-based approaches can be combined with the replica trick using a custom neural-network architecture around a lattice defect connecting two replicas. Numerical tests for the $\phi^4$ scalar field theory in two and three dimensions demonstrate that our technique outperforms state-of-the-art Monte Carlo calculations, and exhibit a promising scaling with the defect size.

Physics-Informed Bayesian Optimization of Variational Quantum Circuits

In this paper, we propose a novel and powerful method to harness Bayesian optimization for Variational Quantum Eigensolvers (VQEs) -- a hybrid quantum-classical protocol used to approximate the ground state of a quantum Hamiltonian. Specifically, we derive a VQE-kernel which incorporates important prior information about quantum circuits: the kernel feature map of the VQE-kernel exactly matches the known functional form of the VQE's objective function and thereby significantly reduces the posterior uncertainty. Moreover, we propose a novel acquisition function for Bayesian optimization called Expected Maximum Improvement over Confident Regions (EMICoRe) which can actively exploit the inductive bias of the VQE-kernel by treating regions with low predictive uncertainty as indirectly ``observed''. As a result, observations at as few as three points in the search domain are sufficient to determine the complete objective function along an entire one-dimensional subspace of the optimization landscape. Our numerical experiments demonstrate that our approach improves over state-of-the-art baselines.

Detecting and Mitigating Mode-Collapse for Flow-based Sampling of Lattice Field Theories

We study the consequences of mode-collapse of normalizing flows in the context of lattice field theory. Normalizing flows allow for independent sampling. For this reason, it is hoped that they can avoid the tunneling problem of local-update MCMC algorithms for multi-modal distributions. In this work, we first point out that the tunneling problem is also present for normalizing flows but is shifted from the sampling to the training phase of the algorithm. Specifically, normalizing flows often suffer from mode-collapse for which the training process assigns vanishingly low probability mass to relevant modes of the physical distribution. This may result in a significant bias when the flow is used as a sampler in a Markov-Chain or with Importance Sampling. We propose a metric to quantify the degree of mode-collapse and derive a bound on the resulting bias. Furthermore, we propose various mitigation strategies in particular in the context of estimating thermodynamic observables, such as the free energy.

Gradients should stay on Path: Better Estimators of the Reverse- and Forward KL Divergence for Normalizing Flows

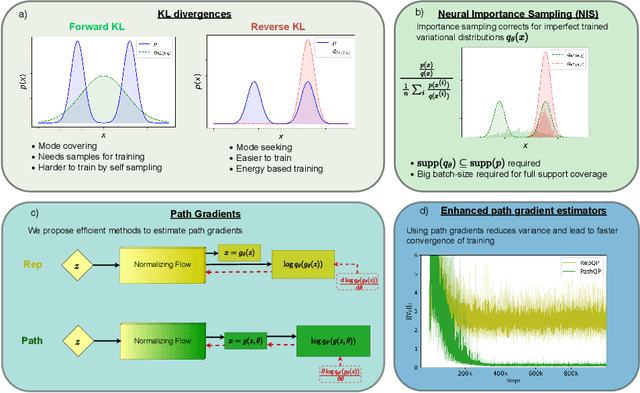
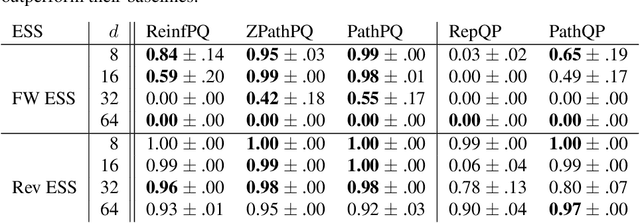
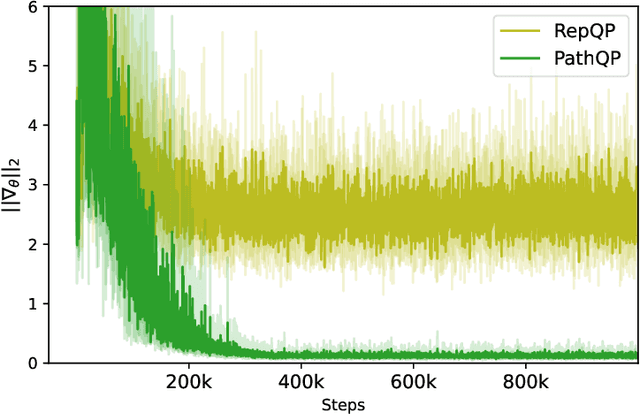
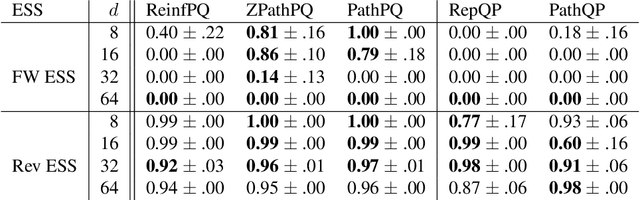
We propose an algorithm to estimate the path-gradient of both the reverse and forward Kullback-Leibler divergence for an arbitrary manifestly invertible normalizing flow. The resulting path-gradient estimators are straightforward to implement, have lower variance, and lead not only to faster convergence of training but also to better overall approximation results compared to standard total gradient estimators. We also demonstrate that path-gradient training is less susceptible to mode-collapse. In light of our results, we expect that path-gradient estimators will become the new standard method to train normalizing flows for variational inference.

Path-Gradient Estimators for Continuous Normalizing Flows

Recent work has established a path-gradient estimator for simple variational Gaussian distributions and has argued that the path-gradient is particularly beneficial in the regime in which the variational distribution approaches the exact target distribution. In many applications, this regime can however not be reached by a simple Gaussian variational distribution. In this work, we overcome this crucial limitation by proposing a path-gradient estimator for the considerably more expressive variational family of continuous normalizing flows. We outline an efficient algorithm to calculate this estimator and establish its superior performance empirically.

Machine Learning of Thermodynamic Observables in the Presence of Mode Collapse

Estimating the free energy, as well as other thermodynamic observables, is a key task in lattice field theories. Recently, it has been pointed out that deep generative models can be used in this context [1]. Crucially, these models allow for the direct estimation of the free energy at a given point in parameter space. This is in contrast to existing methods based on Markov chains which generically require integration through parameter space. In this contribution, we will review this novel machine-learning-based estimation method. We will in detail discuss the issue of mode collapse and outline mitigation techniques which are particularly suited for applications at finite temperature.