Fast and Unified Path Gradient Estimators for Normalizing Flows

Recent work shows that path gradient estimators for normalizing flows have lower variance compared to standard estimators for variational inference, resulting in improved training. However, they are often prohibitively more expensive from a computational point of view and cannot be applied to maximum likelihood training in a scalable manner, which severely hinders their widespread adoption. In this work, we overcome these crucial limitations. Specifically, we propose a fast path gradient estimator which improves computational efficiency significantly and works for all normalizing flow architectures of practical relevance. We then show that this estimator can also be applied to maximum likelihood training for which it has a regularizing effect as it can take the form of a given target energy function into account. We empirically establish its superior performance and reduced variance for several natural sciences applications.

Gradients should stay on Path: Better Estimators of the Reverse- and Forward KL Divergence for Normalizing Flows

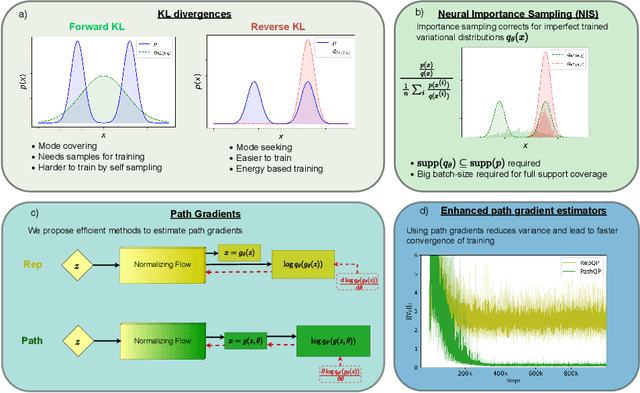
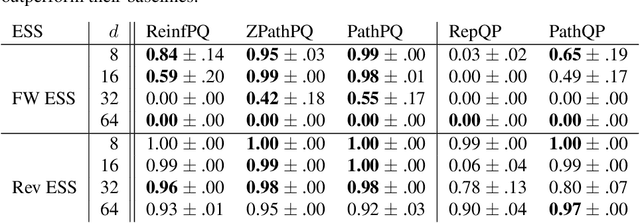
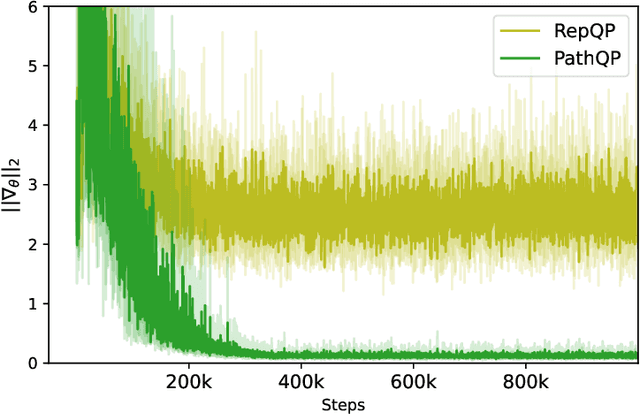
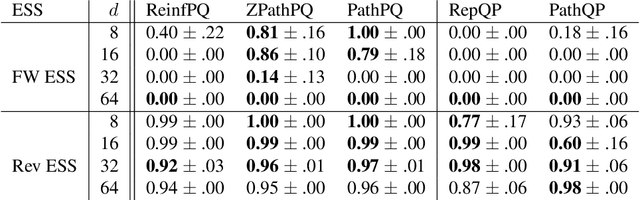
We propose an algorithm to estimate the path-gradient of both the reverse and forward Kullback-Leibler divergence for an arbitrary manifestly invertible normalizing flow. The resulting path-gradient estimators are straightforward to implement, have lower variance, and lead not only to faster convergence of training but also to better overall approximation results compared to standard total gradient estimators. We also demonstrate that path-gradient training is less susceptible to mode-collapse. In light of our results, we expect that path-gradient estimators will become the new standard method to train normalizing flows for variational inference.

Path-Gradient Estimators for Continuous Normalizing Flows

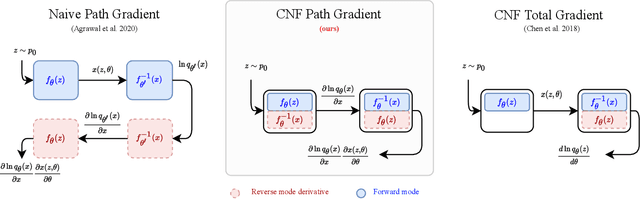
Recent work has established a path-gradient estimator for simple variational Gaussian distributions and has argued that the path-gradient is particularly beneficial in the regime in which the variational distribution approaches the exact target distribution. In many applications, this regime can however not be reached by a simple Gaussian variational distribution. In this work, we overcome this crucial limitation by proposing a path-gradient estimator for the considerably more expressive variational family of continuous normalizing flows. We outline an efficient algorithm to calculate this estimator and establish its superior performance empirically.