Time-Reversible Bridges of Data with Machine Learning

The analysis of dynamical systems is a fundamental tool in the natural sciences and engineering. It is used to understand the evolution of systems as large as entire galaxies and as small as individual molecules. With predefined conditions on the evolution of dy-namical systems, the underlying differential equations have to fulfill specific constraints in time and space. This class of problems is known as boundary value problems. This thesis presents novel approaches to learn time-reversible deterministic and stochastic dynamics constrained by initial and final conditions. The dynamics are inferred by machine learning algorithms from observed data, which is in contrast to the traditional approach of solving differential equations by numerical integration. The work in this thesis examines a set of problems of increasing difficulty each of which is concerned with learning a different aspect of the dynamics. Initially, we consider learning deterministic dynamics from ground truth solutions which are constrained by deterministic boundary conditions. Secondly, we study a boundary value problem in discrete state spaces, where the forward dynamics follow a stochastic jump process and the boundary conditions are discrete probability distributions. In particular, the stochastic dynamics of a specific jump process, the Ehrenfest process, is considered and the reverse time dynamics are inferred with machine learning. Finally, we investigate the problem of inferring the dynamics of a continuous-time stochastic process between two probability distributions without any reference information. Here, we propose a novel criterion to learn time-reversible dynamics of two stochastic processes to solve the Schr\"odinger Bridge Problem.

Bridging discrete and continuous state spaces: Exploring the Ehrenfest process in time-continuous diffusion models

Generative modeling via stochastic processes has led to remarkable empirical results as well as to recent advances in their theoretical understanding. In principle, both space and time of the processes can be discrete or continuous. In this work, we study time-continuous Markov jump processes on discrete state spaces and investigate their correspondence to state-continuous diffusion processes given by SDEs. In particular, we revisit the $\textit{Ehrenfest process}$, which converges to an Ornstein-Uhlenbeck process in the infinite state space limit. Likewise, we can show that the time-reversal of the Ehrenfest process converges to the time-reversed Ornstein-Uhlenbeck process. This observation bridges discrete and continuous state spaces and allows to carry over methods from one to the respective other setting. Additionally, we suggest an algorithm for training the time-reversal of Markov jump processes which relies on conditional expectations and can thus be directly related to denoising score matching. We demonstrate our methods in multiple convincing numerical experiments.

Fast and Unified Path Gradient Estimators for Normalizing Flows

Recent work shows that path gradient estimators for normalizing flows have lower variance compared to standard estimators for variational inference, resulting in improved training. However, they are often prohibitively more expensive from a computational point of view and cannot be applied to maximum likelihood training in a scalable manner, which severely hinders their widespread adoption. In this work, we overcome these crucial limitations. Specifically, we propose a fast path gradient estimator which improves computational efficiency significantly and works for all normalizing flow architectures of practical relevance. We then show that this estimator can also be applied to maximum likelihood training for which it has a regularizing effect as it can take the form of a given target energy function into account. We empirically establish its superior performance and reduced variance for several natural sciences applications.

Super-resolution in Molecular Dynamics Trajectory Reconstruction with Bi-Directional Neural Networks

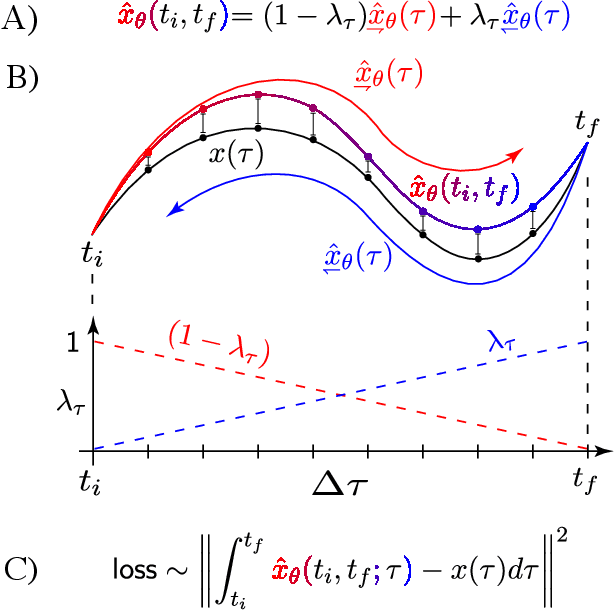
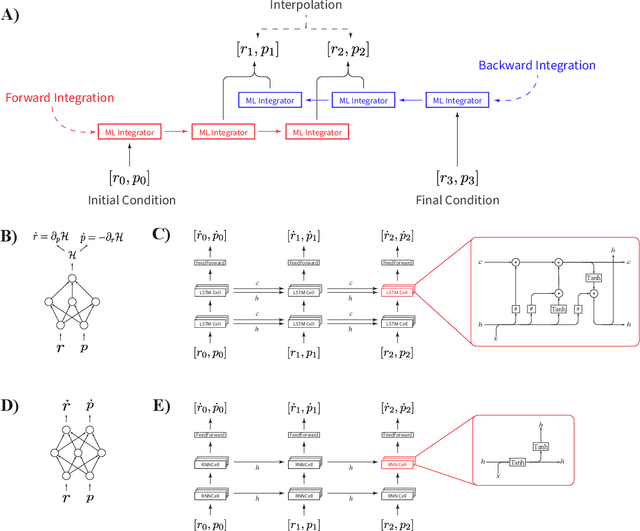
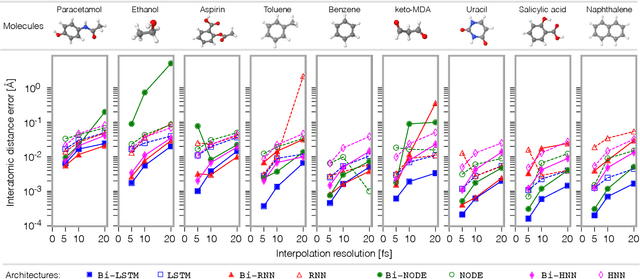
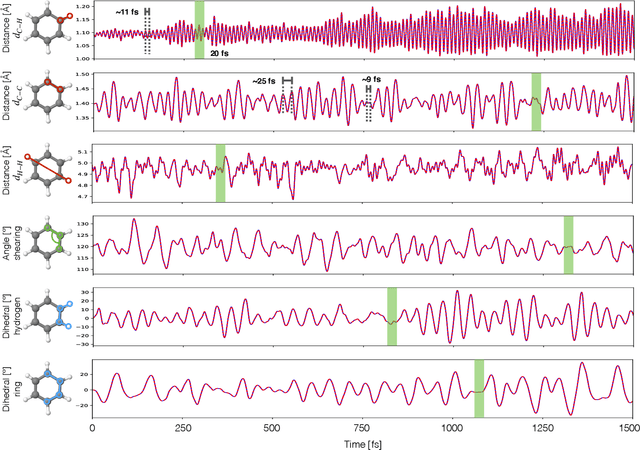
Molecular dynamics simulations are a cornerstone in science, allowing to investigate from the system's thermodynamics to analyse intricate molecular interactions. In general, to create extended molecular trajectories can be a computationally expensive process, for example, when running $ab-initio$ simulations. Hence, repeating such calculations to either obtain more accurate thermodynamics or to get a higher resolution in the dynamics generated by a fine-grained quantum interaction can be time- and computationally-consuming. In this work, we explore different machine learning (ML) methodologies to increase the resolution of molecular dynamics trajectories on-demand within a post-processing step. As a proof of concept, we analyse the performance of bi-directional neural networks such as neural ODEs, Hamiltonian networks, recurrent neural networks and LSTMs, as well as the uni-directional variants as a reference, for molecular dynamics simulations (here: the MD17 dataset). We have found that Bi-LSTMs are the best performing models; by utilizing the local time-symmetry of thermostated trajectories they can even learn long-range correlations and display high robustness to noisy dynamics across molecular complexity. Our models can reach accuracies of up to 10$^{-4}$ angstroms in trajectory interpolation, while faithfully reconstructing several full cycles of unseen intricate high-frequency molecular vibrations, rendering the comparison between the learned and reference trajectories indistinguishable. The results reported in this work can serve (1) as a baseline for larger systems, as well as (2) for the construction of better MD integrators.

Towards CRISP-ML: A Machine Learning Process Model with Quality Assurance Methodology

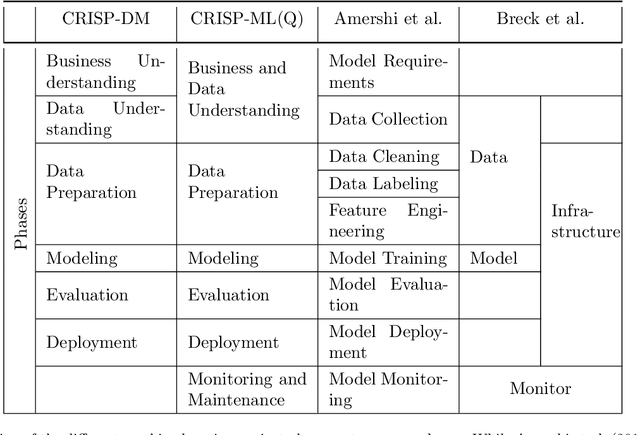
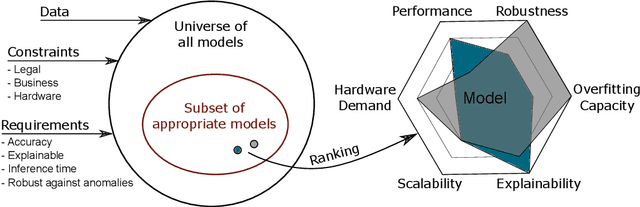
We propose a process model for the development of machine learning applications. It guides machine learning practitioners and project organizations from industry and academia with a checklist of tasks that spans the complete project life-cycle, ranging from the very first idea to the continuous maintenance of any machine learning application. With each task, we propose quality assurance methodology that is drawn from practical experience and scientific literature and that has proven to be general and stable enough to include them in best practices. We expand on CRISP-DM, a data mining process model that enjoys strong industry support but lacks to address machine learning specific tasks.