Towards CRISP-ML: A Machine Learning Process Model with Quality Assurance Methodology

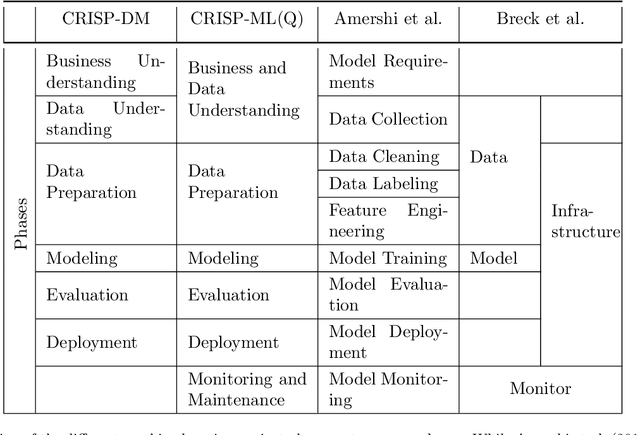
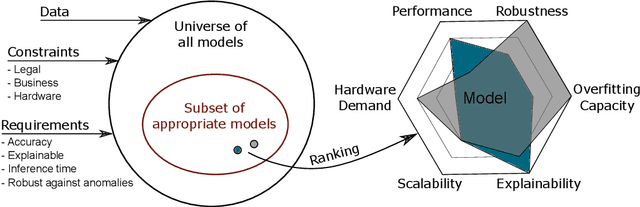
We propose a process model for the development of machine learning applications. It guides machine learning practitioners and project organizations from industry and academia with a checklist of tasks that spans the complete project life-cycle, ranging from the very first idea to the continuous maintenance of any machine learning application. With each task, we propose quality assurance methodology that is drawn from practical experience and scientific literature and that has proven to be general and stable enough to include them in best practices. We expand on CRISP-DM, a data mining process model that enjoys strong industry support but lacks to address machine learning specific tasks.

Sharing Hash Codes for Multiple Purposes

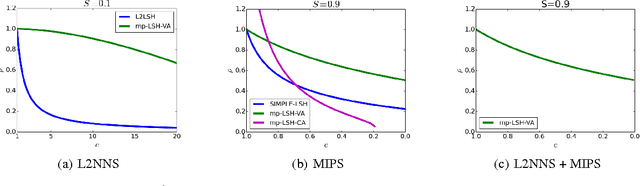
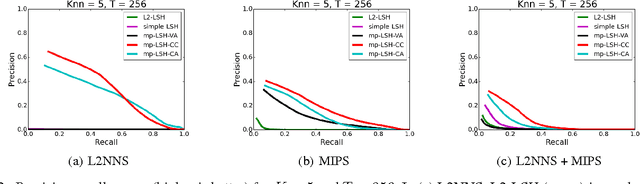
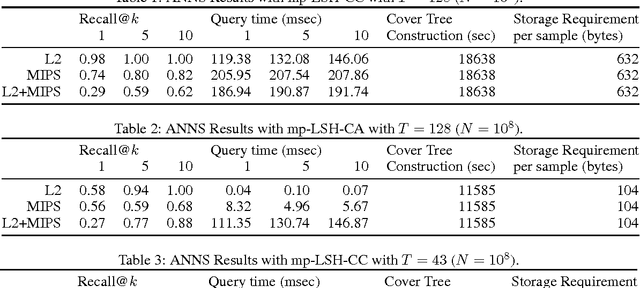
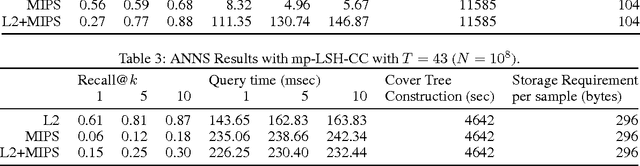
Locality sensitive hashing (LSH) is a powerful tool for sublinear-time approximate nearest neighbor search, and a variety of hashing schemes have been proposed for different dissimilarity measures. However, hash codes significantly depend on the dissimilarity, which prohibits users from adjusting the dissimilarity at query time. In this paper, we propose {multiple purpose LSH (mp-LSH) which shares the hash codes for different dissimilarities. mp-LSH supports L2, cosine, and inner product dissimilarities, and their corresponding weighted sums, where the weights can be adjusted at query time. It also allows us to modify the importance of pre-defined groups of features. Thus, mp-LSH enables us, for example, to retrieve similar items to a query with the user preference taken into account, to find a similar material to a query with some properties (stability, utility, etc.) optimized, and to turn on or off a part of multi-modal information (brightness, color, audio, text, etc.) in image/video retrieval. We theoretically and empirically analyze the performance of three variants of mp-LSH, and demonstrate their usefulness on real-world data sets.

Explorative Data Analysis for Changes in Neural Activity

Neural recordings are nonstationary time series, i.e. their properties typically change over time. Identifying specific changes, e.g. those induced by a learning task, can shed light on the underlying neural processes. However, such changes of interest are often masked by strong unrelated changes, which can be of physiological origin or due to measurement artifacts. We propose a novel algorithm for disentangling such different causes of non-stationarity and in this manner enable better neurophysiological interpretation for a wider set of experimental paradigms. A key ingredient is the repeated application of Stationary Subspace Analysis (SSA) using different temporal scales. The usefulness of our explorative approach is demonstrated in simulations, theory and EEG experiments with 80 Brain-Computer-Interfacing (BCI) subjects.

Algebraic Geometric Comparison of Probability Distributions

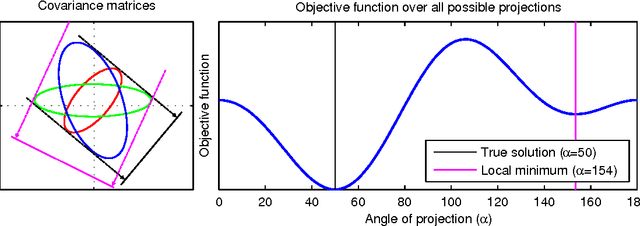
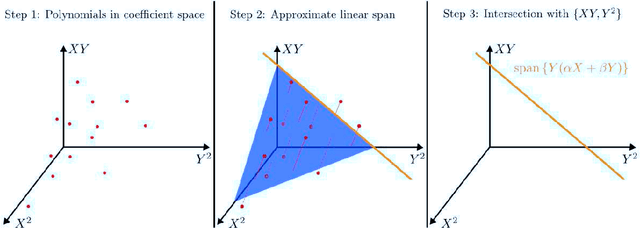
We propose a novel algebraic framework for treating probability distributions represented by their cumulants such as the mean and covariance matrix. As an example, we consider the unsupervised learning problem of finding the subspace on which several probability distributions agree. Instead of minimizing an objective function involving the estimated cumulants, we show that by treating the cumulants as elements of the polynomial ring we can directly solve the problem, at a lower computational cost and with higher accuracy. Moreover, the algebraic viewpoint on probability distributions allows us to invoke the theory of Algebraic Geometry, which we demonstrate in a compact proof for an identifiability criterion.

Modeling sparse connectivity between underlying brain sources for EEG/MEG

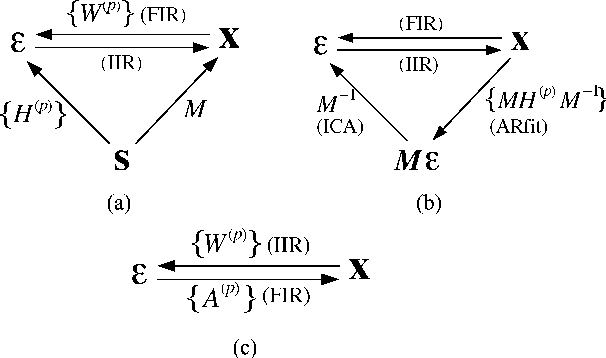
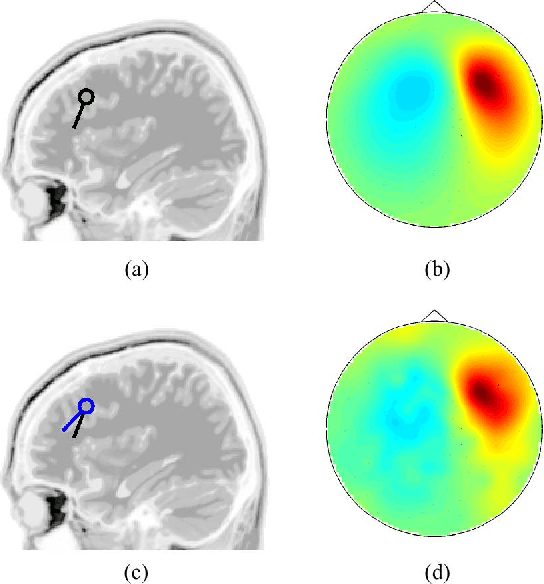
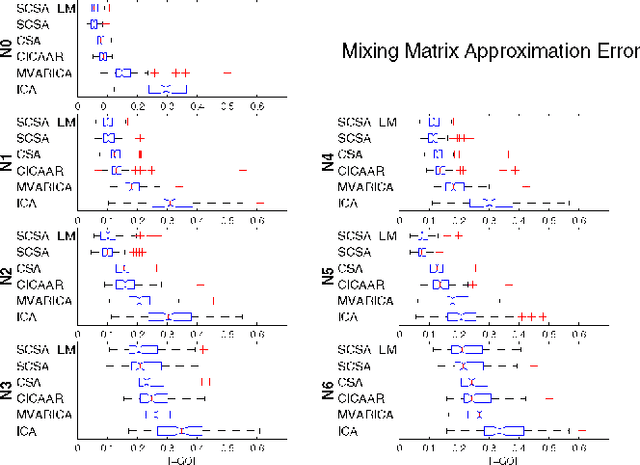
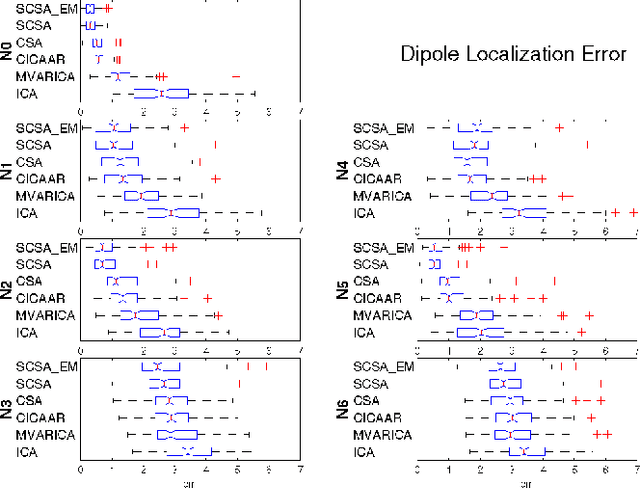
We propose a novel technique to assess functional brain connectivity in EEG/MEG signals. Our method, called Sparsely-Connected Sources Analysis (SCSA), can overcome the problem of volume conduction by modeling neural data innovatively with the following ingredients: (a) the EEG is assumed to be a linear mixture of correlated sources following a multivariate autoregressive (MVAR) model, (b) the demixing is estimated jointly with the source MVAR parameters, (c) overfitting is avoided by using the Group Lasso penalty. This approach allows to extract the appropriate level cross-talk between the extracted sources and in this manner we obtain a sparse data-driven model of functional connectivity. We demonstrate the usefulness of SCSA with simulated data, and compare to a number of existing algorithms with excellent results.

How to Explain Individual Classification Decisions

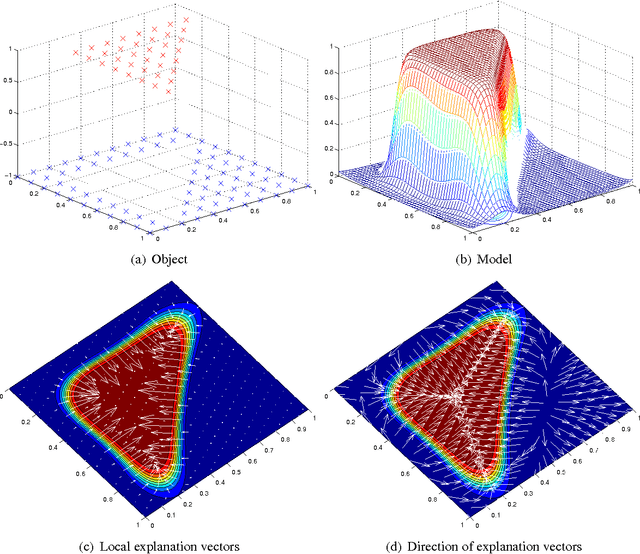
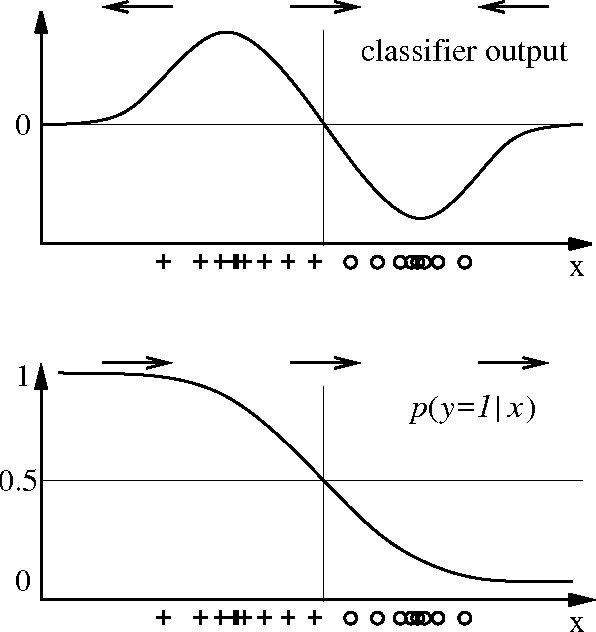
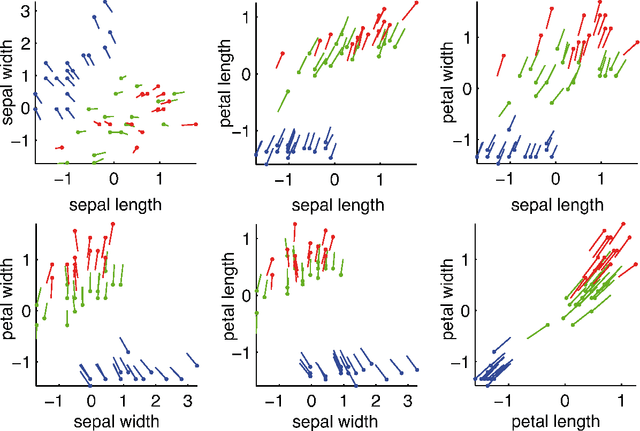
After building a classifier with modern tools of machine learning we typically have a black box at hand that is able to predict well for unseen data. Thus, we get an answer to the question what is the most likely label of a given unseen data point. However, most methods will provide no answer why the model predicted the particular label for a single instance and what features were most influential for that particular instance. The only method that is currently able to provide such explanations are decision trees. This paper proposes a procedure which (based on a set of assumptions) allows to explain the decisions of any classification method.

Sparse Causal Discovery in Multivariate Time Series

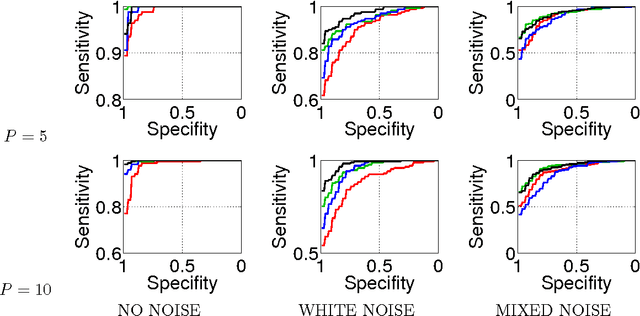
Our goal is to estimate causal interactions in multivariate time series. Using vector autoregressive (VAR) models, these can be defined based on non-vanishing coefficients belonging to respective time-lagged instances. As in most cases a parsimonious causality structure is assumed, a promising approach to causal discovery consists in fitting VAR models with an additional sparsity-promoting regularization. Along this line we here propose that sparsity should be enforced for the subgroups of coefficients that belong to each pair of time series, as the absence of a causal relation requires the coefficients for all time-lags to become jointly zero. Such behavior can be achieved by means of l1-l2-norm regularized regression, for which an efficient active set solver has been proposed recently. Our method is shown to outperform standard methods in recovering simulated causality graphs. The results are on par with a second novel approach which uses multiple statistical testing.