Explorative Data Analysis for Changes in Neural Activity

Neural recordings are nonstationary time series, i.e. their properties typically change over time. Identifying specific changes, e.g. those induced by a learning task, can shed light on the underlying neural processes. However, such changes of interest are often masked by strong unrelated changes, which can be of physiological origin or due to measurement artifacts. We propose a novel algorithm for disentangling such different causes of non-stationarity and in this manner enable better neurophysiological interpretation for a wider set of experimental paradigms. A key ingredient is the repeated application of Stationary Subspace Analysis (SSA) using different temporal scales. The usefulness of our explorative approach is demonstrated in simulations, theory and EEG experiments with 80 Brain-Computer-Interfacing (BCI) subjects.

Algebraic Geometric Comparison of Probability Distributions

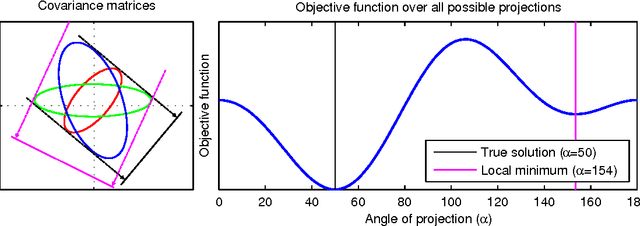
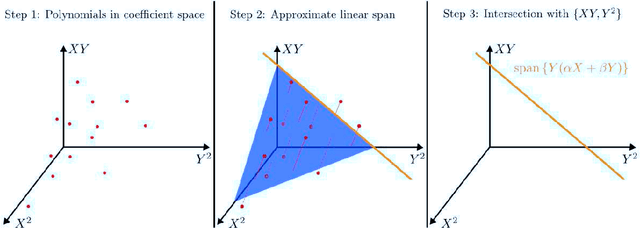
We propose a novel algebraic framework for treating probability distributions represented by their cumulants such as the mean and covariance matrix. As an example, we consider the unsupervised learning problem of finding the subspace on which several probability distributions agree. Instead of minimizing an objective function involving the estimated cumulants, we show that by treating the cumulants as elements of the polynomial ring we can directly solve the problem, at a lower computational cost and with higher accuracy. Moreover, the algebraic viewpoint on probability distributions allows us to invoke the theory of Algebraic Geometry, which we demonstrate in a compact proof for an identifiability criterion.