Prediction and Quantification of Individual Athletic Performance

We provide scientific foundations for athletic performance prediction on an individual level, exposing the phenomenology of individual athletic running performance in the form of a low-rank model dominated by an individual power law. We present, evaluate, and compare a selection of methods for prediction of individual running performance, including our own, \emph{local matrix completion} (LMC), which we show to perform best. We also show that many documented phenomena in quantitative sports science, such as the form of scoring tables, the success of existing prediction methods including Riegel's formula, the Purdy points scheme, the power law for world records performances and the broken power law for world record speeds may be explained on the basis of our findings in a unified way.

Algebraic-Combinatorial Methods for Low-Rank Matrix Completion with Application to Athletic Performance Prediction

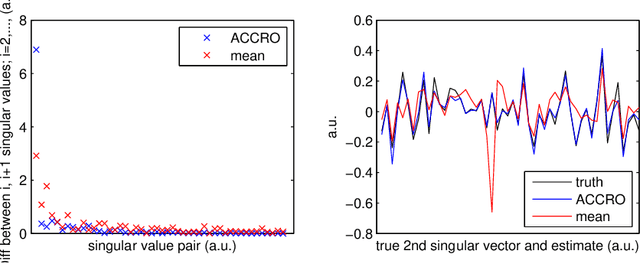
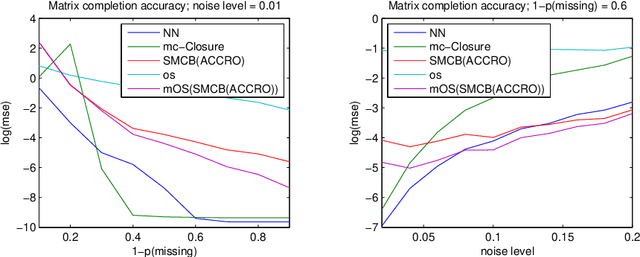
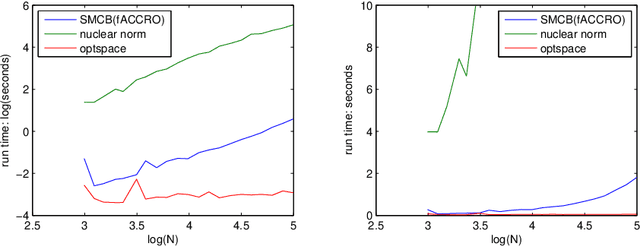
This paper presents novel algorithms which exploit the intrinsic algebraic and combinatorial structure of the matrix completion task for estimating missing en- tries in the general low rank setting. For positive data, we achieve results out- performing the state of the art nuclear norm, both in accuracy and computational efficiency, in simulations and in the task of predicting athletic performance from partially observed data.

Explorative Data Analysis for Changes in Neural Activity

Neural recordings are nonstationary time series, i.e. their properties typically change over time. Identifying specific changes, e.g. those induced by a learning task, can shed light on the underlying neural processes. However, such changes of interest are often masked by strong unrelated changes, which can be of physiological origin or due to measurement artifacts. We propose a novel algorithm for disentangling such different causes of non-stationarity and in this manner enable better neurophysiological interpretation for a wider set of experimental paradigms. A key ingredient is the repeated application of Stationary Subspace Analysis (SSA) using different temporal scales. The usefulness of our explorative approach is demonstrated in simulations, theory and EEG experiments with 80 Brain-Computer-Interfacing (BCI) subjects.

Algebraic Geometric Comparison of Probability Distributions

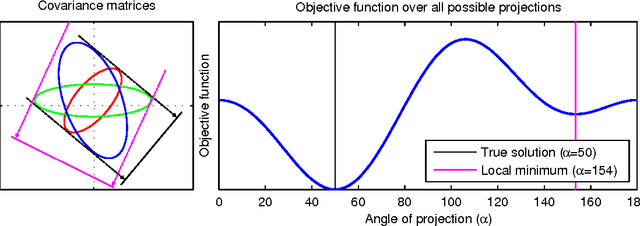
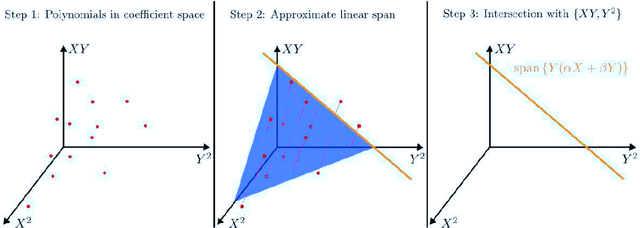
We propose a novel algebraic framework for treating probability distributions represented by their cumulants such as the mean and covariance matrix. As an example, we consider the unsupervised learning problem of finding the subspace on which several probability distributions agree. Instead of minimizing an objective function involving the estimated cumulants, we show that by treating the cumulants as elements of the polynomial ring we can directly solve the problem, at a lower computational cost and with higher accuracy. Moreover, the algebraic viewpoint on probability distributions allows us to invoke the theory of Algebraic Geometry, which we demonstrate in a compact proof for an identifiability criterion.

Two Projection Pursuit Algorithms for Machine Learning under Non-Stationarity

This thesis derives, tests and applies two linear projection algorithms for machine learning under non-stationarity. The first finds a direction in a linear space upon which a data set is maximally non-stationary. The second aims to robustify two-way classification against non-stationarity. The algorithm is tested on a key application scenario, namely Brain Computer Interfacing.