Designing Machine Learning Toolboxes: Concepts, Principles and Patterns

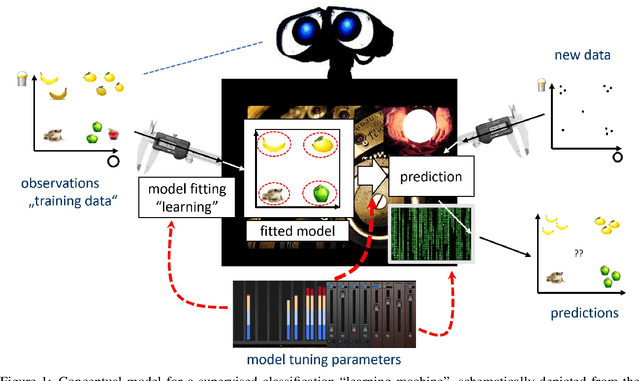
Machine learning (ML) and AI toolboxes such as scikit-learn or Weka are workhorses of contemporary data scientific practice -- their central role being enabled by usable yet powerful designs that allow to easily specify, train and validate complex modeling pipelines. However, despite their universal success, the key design principles in their construction have never been fully analyzed. In this paper, we attempt to provide an overview of key patterns in the design of AI modeling toolboxes, taking inspiration, in equal parts, from the field of software engineering, implementation patterns found in contemporary toolboxes, and our own experience from developing ML toolboxes. In particular, we develop a conceptual model for the AI/ML domain, with a new type system, called scientific types, at its core. Scientific types capture the scientific meaning of common elements in ML workflows based on the set of operations that we usually perform with them (i.e. their interface) and their statistical properties. From our conceptual analysis, we derive a set of design principles and patterns. We illustrate that our analysis can not only explain the design of existing toolboxes, but also guide the development of new ones. We intend our contribution to be a state-of-art reference for future toolbox engineers, a summary of best practices, a collection of ML design patterns which may become useful for future research, and, potentially, the first steps towards a higher-level programming paradigm for constructing AI.

mlr3proba: Machine Learning Survival Analysis in R

As machine learning has become increasingly popular over the last few decades, so too has the number of machine learning interfaces for implementing these models. However, no consistent interface for evaluation and modelling of survival analysis has emerged despite its vital importance in many fields, including medicine, economics, and engineering. \texttt{mlr3proba} is part of the \texttt{mlr3} ecosystem of machine learning packages for R and facilitates \texttt{mlr3}'s general model tuning and benchmarking by providing a multitude of performance measures and learners for survival analysis with a clean and systematic infrastructure for their evaluation. \texttt{mlr3proba} provides a comprehensive machine learning interface for survival analysis, which allows survival modelling to finally be up to the state-of-art.

Kernels for time series with irregularly-spaced multivariate observations

Time series are an interesting frontier for kernel-based methods, for the simple reason that there is no kernel designed to represent them and their unique characteristics in full generality. Existing sequential kernels ignore the time indices, with many assuming that the series must be regularly-spaced; some such kernels are not even psd. In this manuscript, we show that a "series kernel" that is general enough to represent irregularly-spaced multivariate time series may be built out of well-known "vector kernels". We also show that all series kernels constructed using our methodology are psd, and are thus widely applicable. We demonstrate this point by formulating a Gaussian process-based strategy - with our series kernel at its heart - to make predictions about test series when given a training set. We validate the strategy experimentally by estimating its generalisation error on multiple datasets and comparing it to relevant baselines. We also demonstrate that our series kernel may be used for the more traditional setting of time series classification, where its performance is broadly in line with alternative methods.

sktime: A Unified Interface for Machine Learning with Time Series

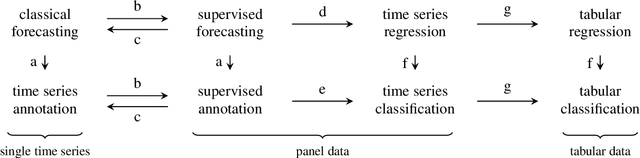
We present sktime -- a new scikit-learn compatible Python library with a unified interface for machine learning with time series. Time series data gives rise to various distinct but closely related learning tasks, such as forecasting and time series classification, many of which can be solved by reducing them to related simpler tasks. We discuss the main rationale for creating a unified interface, including reduction, as well as the design of sktime's core API, supported by a clear overview of common time series tasks and reduction approaches.

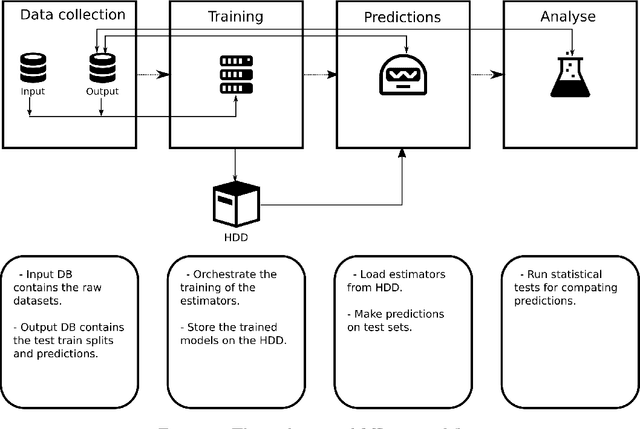
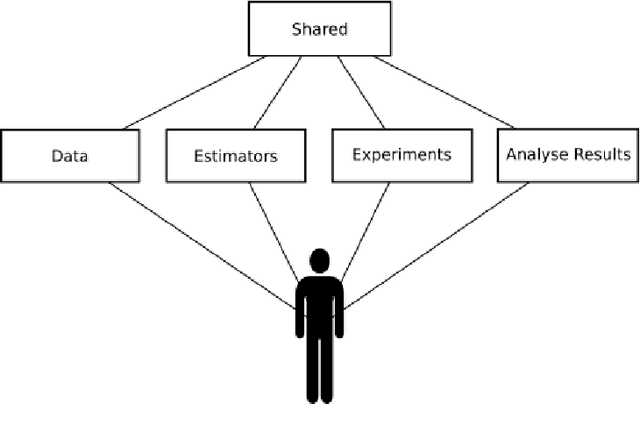
Machine Learning Automation Toolbox (MLaut)

In this paper we present MLaut (Machine Learning AUtomation Toolbox) for the python data science ecosystem. MLaut automates large-scale evaluation and benchmarking of machine learning algorithms on a large number of datasets. MLaut provides a high-level workflow interface to machine algorithm algorithms, implements a local back-end to a database of dataset collections, trained algorithms, and experimental results, and provides easy-to-use interfaces to the scikit-learn and keras modelling libraries. Experiments are easy to set up with default settings in a few lines of code, while remaining fully customizable to the level of hyper-parameter tuning, pipeline composition, or deep learning architecture. As a principal test case for MLaut, we conducted a large-scale supervised classification study in order to benchmark the performance of a number of machine learning algorithms - to our knowledge also the first larger-scale study on standard supervised learning data sets to include deep learning algorithms. While corroborating a number of previous findings in literature, we found (within the limitations of our study) that deep neural networks do not perform well on basic supervised learning, i.e., outside the more specialized, image-, audio-, or text-based tasks.

Modeling outcomes of soccer matches

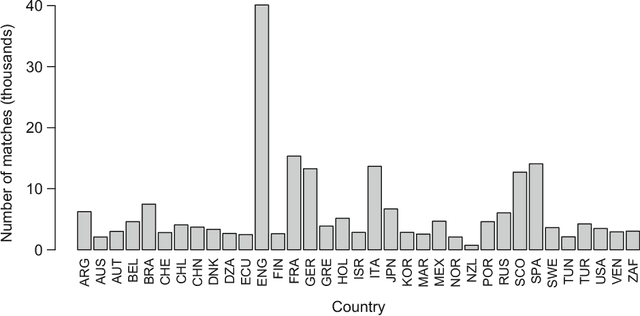
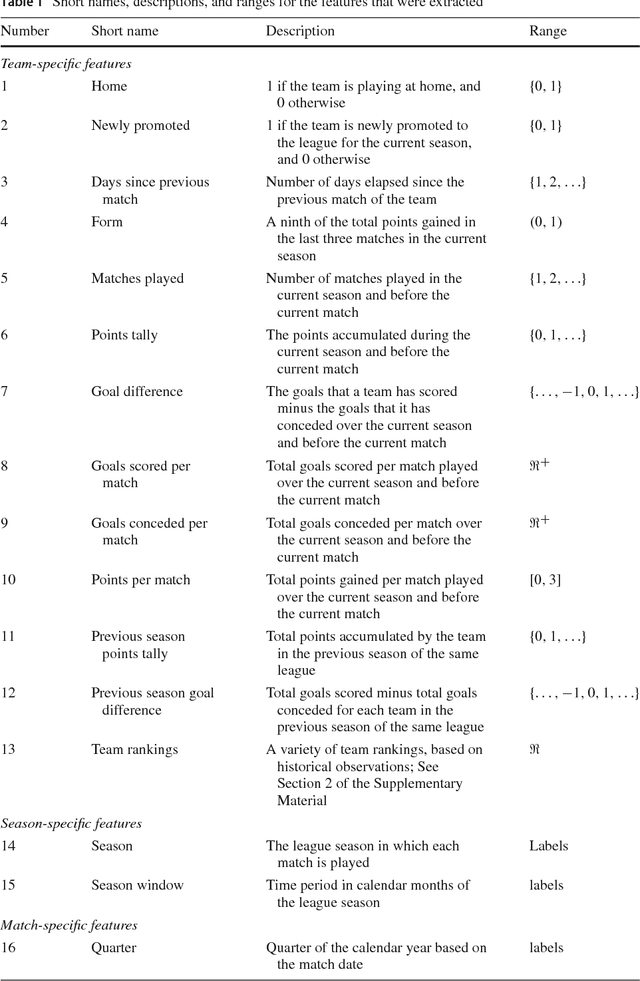
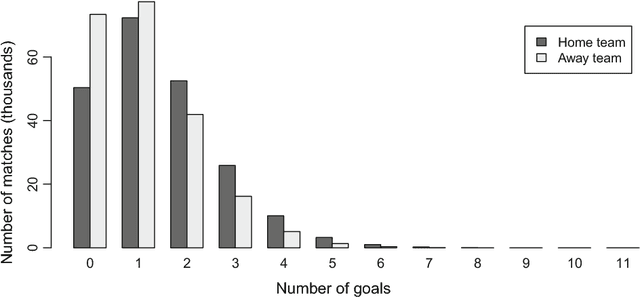
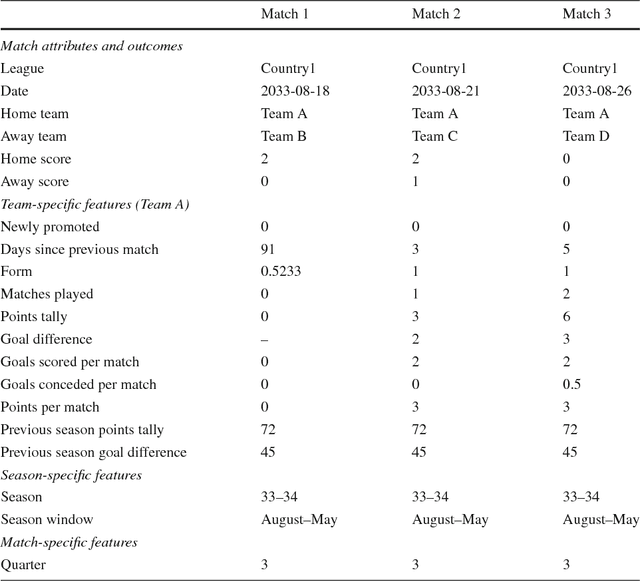
We compare various extensions of the Bradley-Terry model and a hierarchical Poisson log-linear model in terms of their performance in predicting the outcome of soccer matches (win, draw, or loss). The parameters of the Bradley-Terry extensions are estimated by maximizing the log-likelihood, or an appropriately penalized version of it, while the posterior densities of the parameters of the hierarchical Poisson log-linear model are approximated using integrated nested Laplace approximations. The prediction performance of the various modeling approaches is assessed using a novel, context-specific framework for temporal validation that is found to deliver accurate estimates of the test error. The direct modeling of outcomes via the various Bradley-Terry extensions and the modeling of match scores using the hierarchical Poisson log-linear model demonstrate similar behavior in terms of predictive performance.

Probabilistic supervised learning

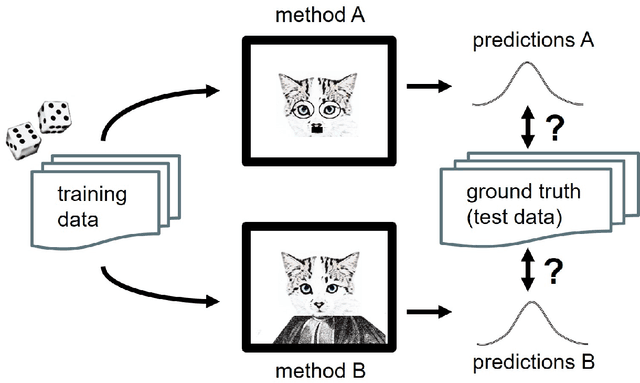
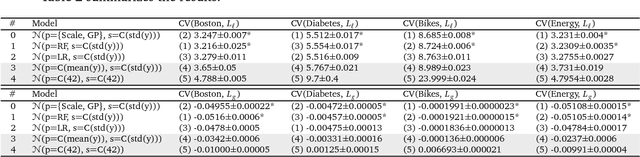
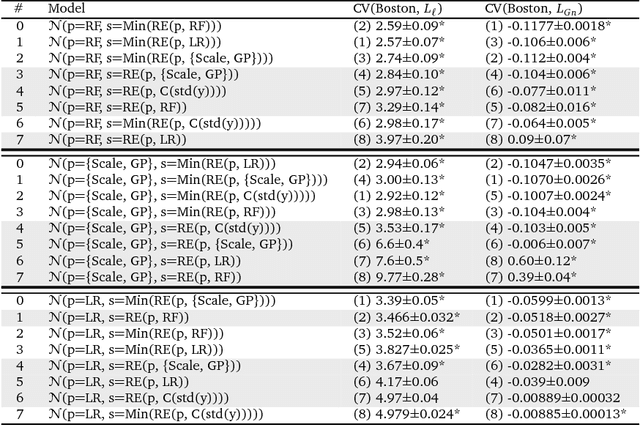
Predictive modelling and supervised learning are central to modern data science. With predictions from an ever-expanding number of supervised black-box strategies - e.g., kernel methods, random forests, deep learning aka neural networks - being employed as a basis for decision making processes, it is crucial to understand the statistical uncertainty associated with these predictions. As a general means to approach the issue, we present an overarching framework for black-box prediction strategies that not only predict the target but also their own predictions' uncertainty. Moreover, the framework allows for fair assessment and comparison of disparate prediction strategies. For this, we formally consider strategies capable of predicting full distributions from feature variables, so-called probabilistic supervised learning strategies. Our work draws from prior work including Bayesian statistics, information theory, and modern supervised machine learning, and in a novel synthesis leads to (a) new theoretical insights such as a probabilistic bias-variance decomposition and an entropic formulation of prediction, as well as to (b) new algorithms and meta-algorithms, such as composite prediction strategies, probabilistic boosting and bagging, and a probabilistic predictive independence test. Our black-box formulation also leads (c) to a new modular interface view on probabilistic supervised learning and a modelling workflow API design, which we have implemented in the newly released skpro machine learning toolbox, extending the familiar modelling interface and meta-modelling functionality of sklearn. The skpro package provides interfaces for construction, composition, and tuning of probabilistic supervised learning strategies, together with orchestration features for validation and comparison of any such strategy - be it frequentist, Bayesian, or other.

Modelling Competitive Sports: Bradley-Terry-Élő Models for Supervised and On-Line Learning of Paired Competition Outcomes

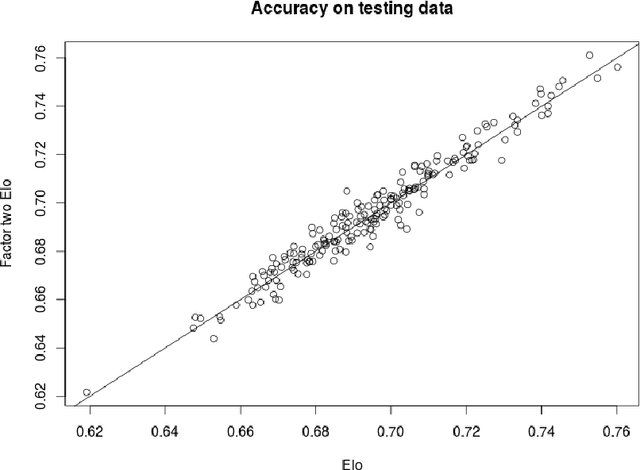
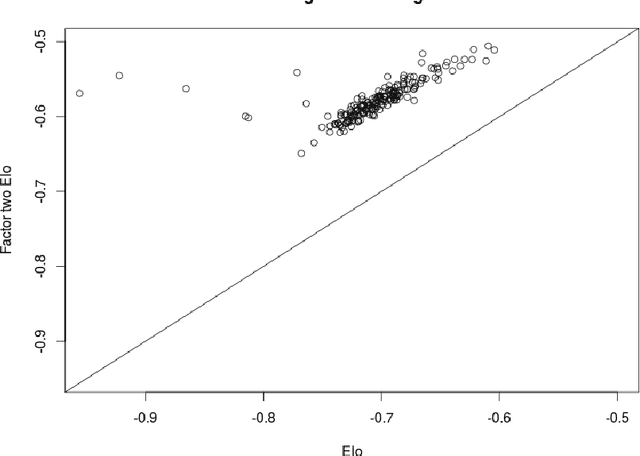
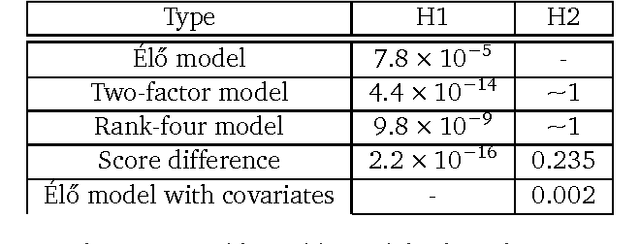
Prediction and modelling of competitive sports outcomes has received much recent attention, especially from the Bayesian statistics and machine learning communities. In the real world setting of outcome prediction, the seminal \'{E}l\H{o} update still remains, after more than 50 years, a valuable baseline which is difficult to improve upon, though in its original form it is a heuristic and not a proper statistical "model". Mathematically, the \'{E}l\H{o} rating system is very closely related to the Bradley-Terry models, which are usually used in an explanatory fashion rather than in a predictive supervised or on-line learning setting. Exploiting this close link between these two model classes and some newly observed similarities, we propose a new supervised learning framework with close similarities to logistic regression, low-rank matrix completion and neural networks. Building on it, we formulate a class of structured log-odds models, unifying the desirable properties found in the above: supervised probabilistic prediction of scores and wins/draws/losses, batch/epoch and on-line learning, as well as the possibility to incorporate features in the prediction, without having to sacrifice simplicity, parsimony of the Bradley-Terry models, or computational efficiency of \'{E}l\H{o}'s original approach. We validate the structured log-odds modelling approach in synthetic experiments and English Premier League outcomes, where the added expressivity yields the best predictions reported in the state-of-art, close to the quality of contemporary betting odds.

Prediction and Quantification of Individual Athletic Performance

We provide scientific foundations for athletic performance prediction on an individual level, exposing the phenomenology of individual athletic running performance in the form of a low-rank model dominated by an individual power law. We present, evaluate, and compare a selection of methods for prediction of individual running performance, including our own, \emph{local matrix completion} (LMC), which we show to perform best. We also show that many documented phenomena in quantitative sports science, such as the form of scoring tables, the success of existing prediction methods including Riegel's formula, the Purdy points scheme, the power law for world records performances and the broken power law for world record speeds may be explained on the basis of our findings in a unified way.

Learning with Algebraic Invariances, and the Invariant Kernel Trick

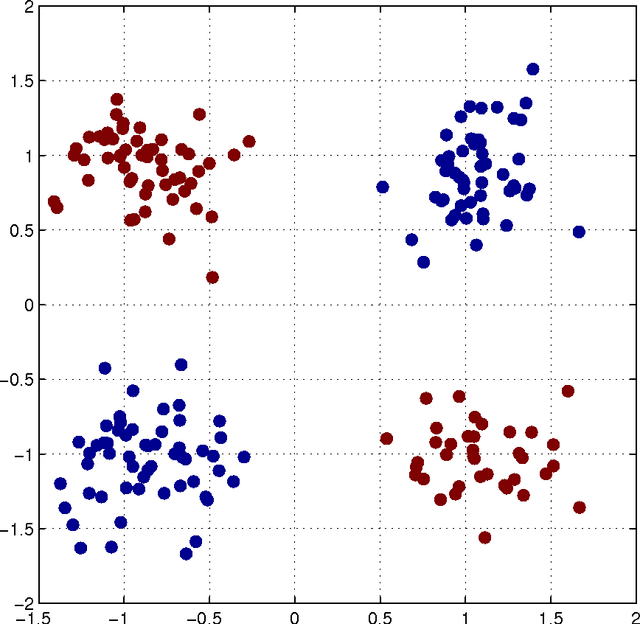
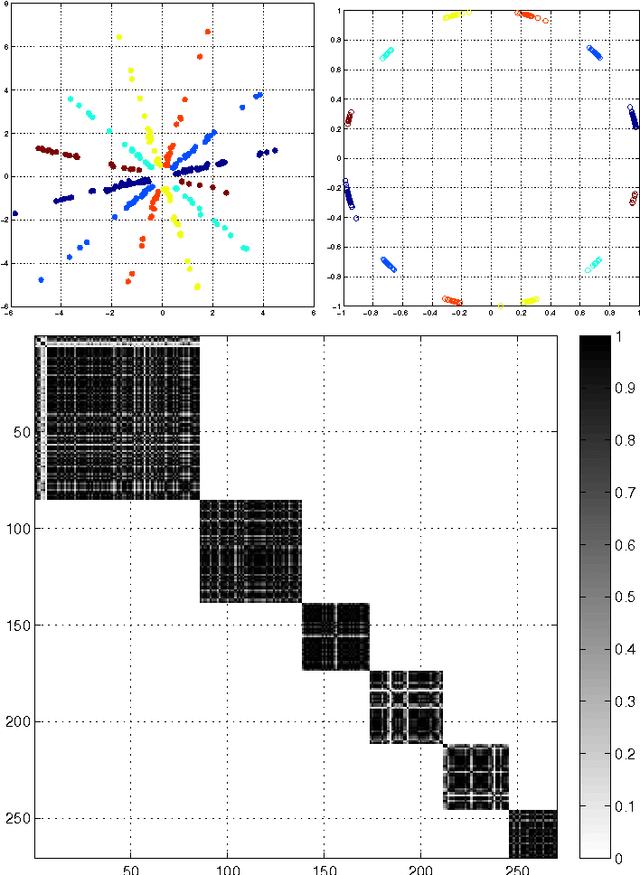
When solving data analysis problems it is important to integrate prior knowledge and/or structural invariances. This paper contributes by a novel framework for incorporating algebraic invariance structure into kernels. In particular, we show that algebraic properties such as sign symmetries in data, phase independence, scaling etc. can be included easily by essentially performing the kernel trick twice. We demonstrate the usefulness of our theory in simulations on selected applications such as sign-invariant spectral clustering and underdetermined ICA.