Counterfactual Learning with Multioutput Deep Kernels

In this paper, we address the challenge of performing counterfactual inference with observational data via Bayesian nonparametric regression adjustment, with a focus on high-dimensional settings featuring multiple actions and multiple correlated outcomes. We present a general class of counterfactual multi-task deep kernels models that estimate causal effects and learn policies proficiently thanks to their sample efficiency gains, while scaling well with high dimensions. In the first part of the work, we rely on Structural Causal Models (SCM) to formally introduce the setup and the problem of identifying counterfactual quantities under observed confounding. We then discuss the benefits of tackling the task of causal effects estimation via stacked coregionalized Gaussian Processes and Deep Kernels. Finally, we demonstrate the use of the proposed methods on simulated experiments that span individual causal effects estimation, off-policy evaluation and optimization.

Interpretable Deep Causal Learning for Moderation Effects

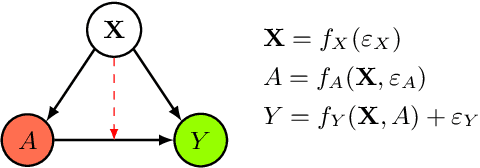
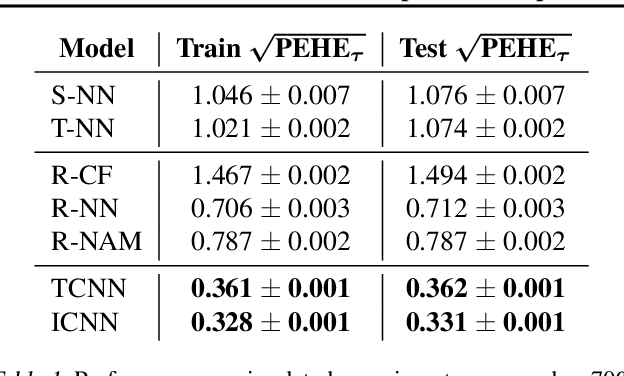
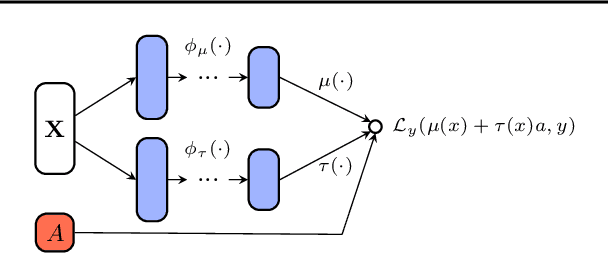
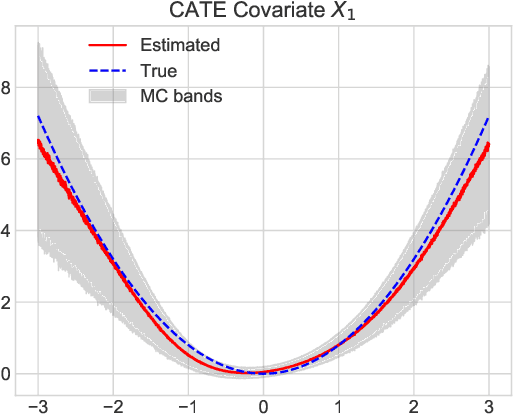
In this extended abstract paper, we address the problem of interpretability and targeted regularization in causal machine learning models. In particular, we focus on the problem of estimating individual causal/treatment effects under observed confounders, which can be controlled for and moderate the effect of the treatment on the outcome of interest. Black-box ML models adjusted for the causal setting perform generally well in this task, but they lack interpretable output identifying the main drivers of treatment heterogeneity and their functional relationship. We propose a novel deep counterfactual learning architecture for estimating individual treatment effects that can simultaneously: i) convey targeted regularization on, and produce quantify uncertainty around the quantity of interest (i.e., the Conditional Average Treatment Effect); ii) disentangle baseline prognostic and moderating effects of the covariates and output interpretable score functions describing their relationship with the outcome. Finally, we demonstrate the use of the method via a simple simulated experiment.

Sparse Bayesian Causal Forests for Heterogeneous Treatment Effects Estimation

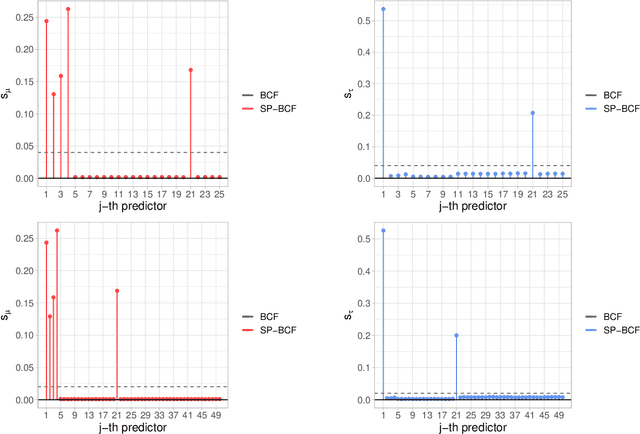
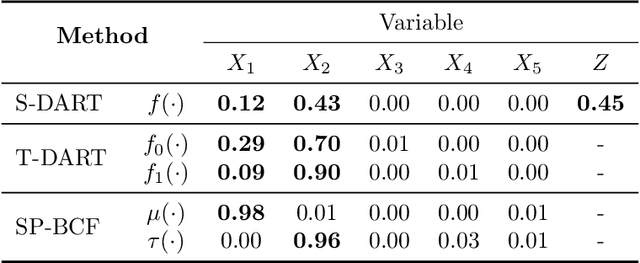
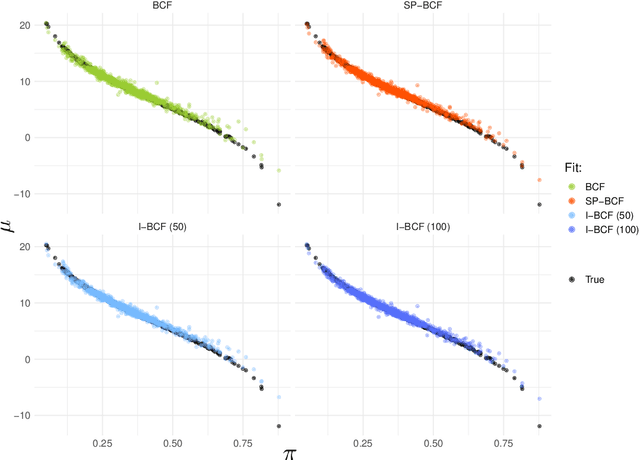
This paper develops a sparsity-inducing version of Bayesian Causal Forests, a recently proposed nonparametric causal regression model that employs Bayesian Additive Regression Trees and is specifically designed to estimate heterogeneous treatment effects using observational data. The sparsity-inducing component we introduce is motivated by empirical studies where the number of pre-treatment covariates available is non-negligible, leading to different degrees of sparsity underlying the surfaces of interest in the estimation of individual treatment effects. The extended version presented in this work, which we name Sparse Bayesian Causal Forest, is equipped with an additional pair of priors allowing the model to adjust the weight of each covariate through the corresponding number of splits in the tree ensemble. These priors improve the model's adaptability to sparse settings and allow to perform fully Bayesian variable selection in a framework for treatment effects estimation, and thus to uncover the moderating factors driving heterogeneity. In addition, the method allows prior knowledge about the relevant confounding pre-treatment covariates and the relative magnitude of their impact on the outcome to be incorporated in the model. We illustrate the performance of our method in simulated studies, in comparison to Bayesian Causal Forest and other state-of-the-art models, to demonstrate how it scales up with an increasing number of covariates and how it handles strongly confounded scenarios. Finally, we also provide an example of application using real-world data.

Estimating Individual Treatment Effects using Non-Parametric Regression Models: a Review

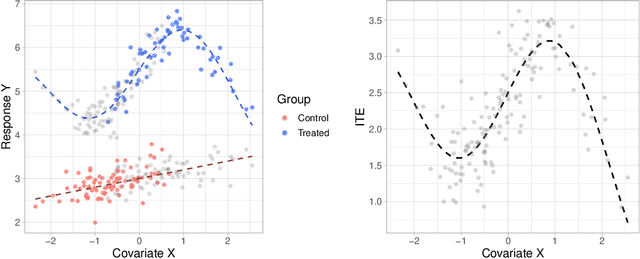
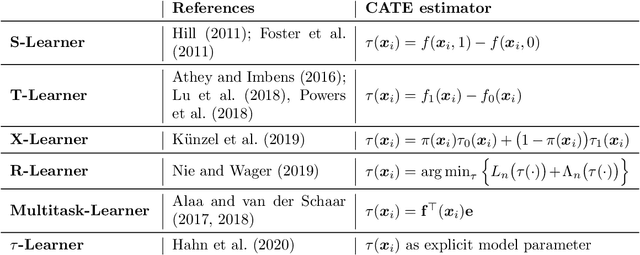
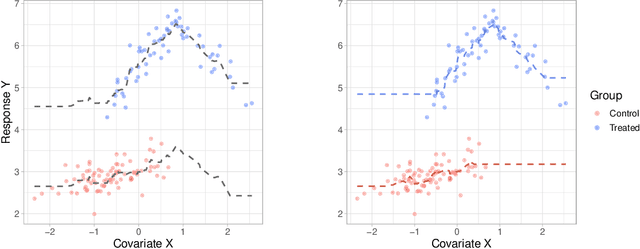
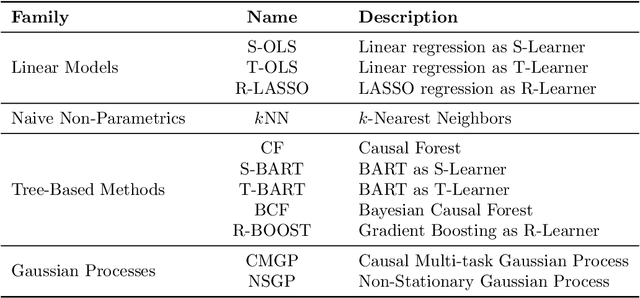
Large observational data are increasingly available in disciplines such as health, economic and social sciences, where researchers are interested in causal questions rather than prediction. In this paper, we investigate the problem of estimating heterogeneous treatment effects using non-parametric regression-based methods. Firstly, we introduce the setup and the issues related to conducting causal inference with observational or non-fully randomized data, and how these issues can be tackled with the help of statistical learning tools. Then, we provide a review of state-of-the-art methods, with a particular focus on non-parametric modeling, and we cast them under a unifying taxonomy. After presenting a brief overview on the problem of model selection, we illustrate the performance of some of the methods on three different simulated studies and on a real world example to investigate the effect of participation in school meal programs on health indicators.

Modeling outcomes of soccer matches

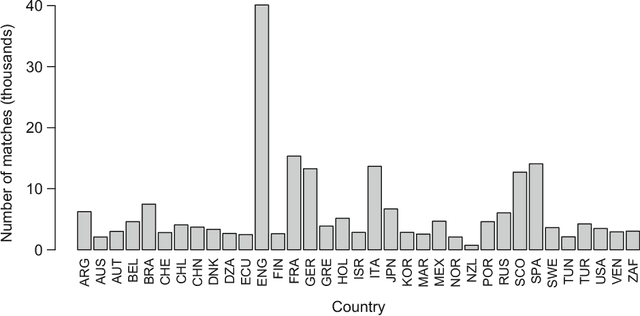
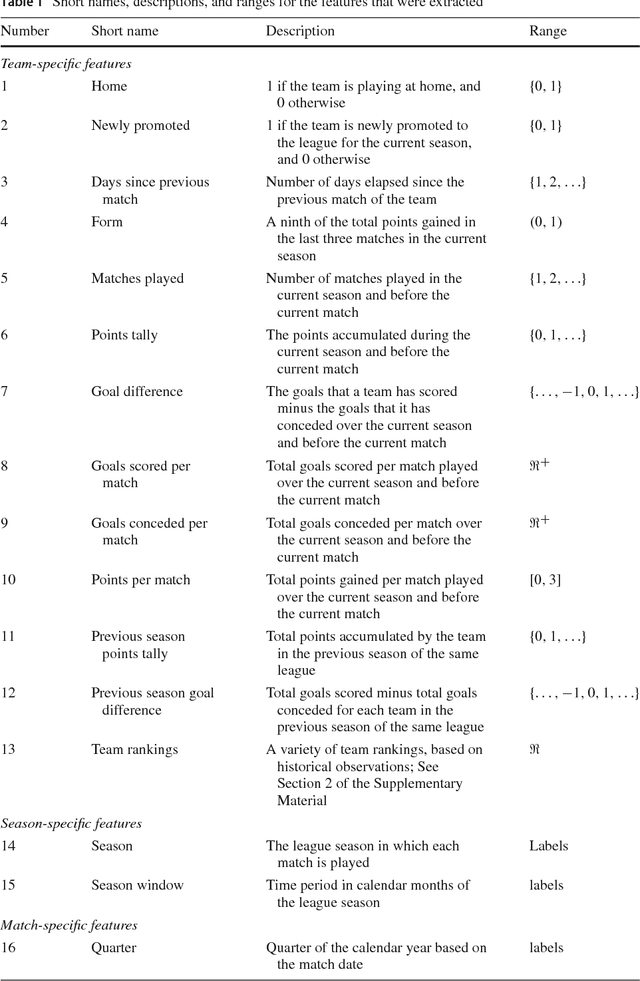
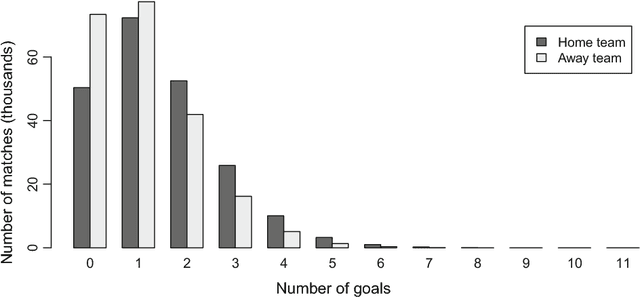
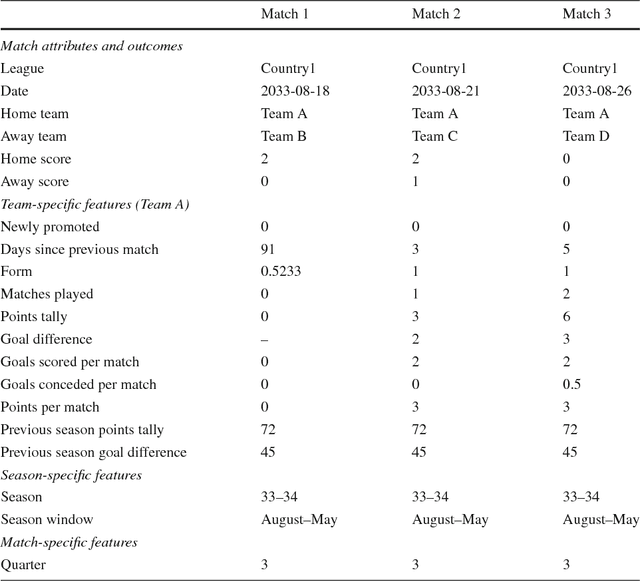
We compare various extensions of the Bradley-Terry model and a hierarchical Poisson log-linear model in terms of their performance in predicting the outcome of soccer matches (win, draw, or loss). The parameters of the Bradley-Terry extensions are estimated by maximizing the log-likelihood, or an appropriately penalized version of it, while the posterior densities of the parameters of the hierarchical Poisson log-linear model are approximated using integrated nested Laplace approximations. The prediction performance of the various modeling approaches is assessed using a novel, context-specific framework for temporal validation that is found to deliver accurate estimates of the test error. The direct modeling of outcomes via the various Bradley-Terry extensions and the modeling of match scores using the hierarchical Poisson log-linear model demonstrate similar behavior in terms of predictive performance.