Inherently Interpretable and Uncertainty-Aware Models for Online Learning in Cyber-Security Problems

In this paper, we address the critical need for interpretable and uncertainty-aware machine learning models in the context of online learning for high-risk industries, particularly cyber-security. While deep learning and other complex models have demonstrated impressive predictive capabilities, their opacity and lack of uncertainty quantification present significant questions about their trustworthiness. We propose a novel pipeline for online supervised learning problems in cyber-security, that harnesses the inherent interpretability and uncertainty awareness of Additive Gaussian Processes (AGPs) models. Our approach aims to balance predictive performance with transparency while improving the scalability of AGPs, which represents their main drawback, potentially enabling security analysts to better validate threat detection, troubleshoot and reduce false positives, and generally make trustworthy, informed decisions. This work contributes to the growing field of interpretable AI by proposing a class of models that can be significantly beneficial for high-stake decision problems such as the ones typical of the cyber-security domain. The source code is available.

Entity-based Reinforcement Learning for Autonomous Cyber Defence

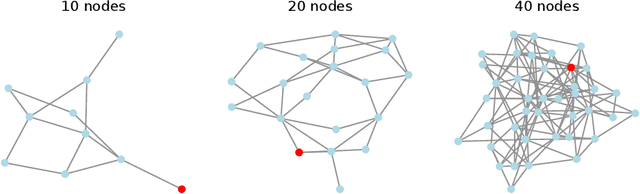
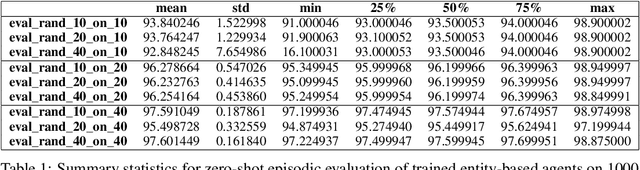
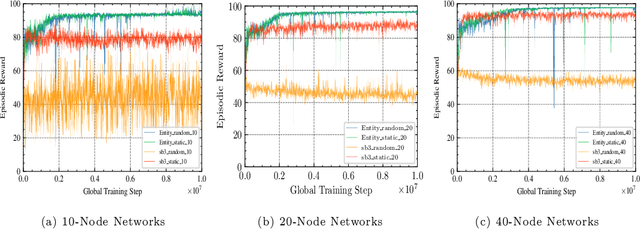
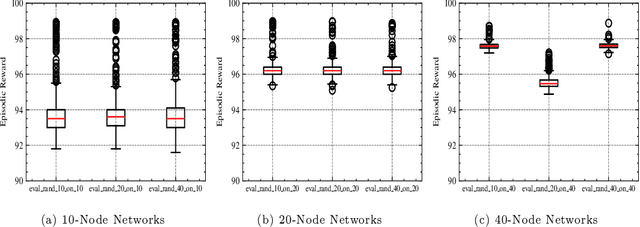
A significant challenge for autonomous cyber defence is ensuring a defensive agent's ability to generalise across diverse network topologies and configurations. This capability is necessary for agents to remain effective when deployed in dynamically changing environments, such as an enterprise network where devices may frequently join and leave. Standard approaches to deep reinforcement learning, where policies are parameterised using a fixed-input multi-layer perceptron (MLP) expect fixed-size observation and action spaces. In autonomous cyber defence, this makes it hard to develop agents that generalise to environments with network topologies different from those trained on, as the number of nodes affects the natural size of the observation and action spaces. To overcome this limitation, we reframe the problem of autonomous network defence using entity-based reinforcement learning, where the observation and action space of an agent are decomposed into a collection of discrete entities. This framework enables the use of policy parameterisations specialised in compositional generalisation. Namely, we train a Transformer-based policy on the Yawning Titan cyber-security simulation environment and test its generalisation capabilities across various network topologies. We demonstrate that this approach significantly outperforms an MLP-based policy on fixed networks, and has the ability for zero-shot generalisation to networks of a different size to those seen in training. These findings highlight the potential for entity-based reinforcement learning to advance the field of autonomous cyber defence by providing more generalisable policies capable of handling variations in real-world network environments.

A View on Out-of-Distribution Identification from a Statistical Testing Theory Perspective

We study the problem of efficiently detecting Out-of-Distribution (OOD) samples at test time in supervised and unsupervised learning contexts. While ML models are typically trained under the assumption that training and test data stem from the same distribution, this is often not the case in realistic settings, thus reliably detecting distribution shifts is crucial at deployment. We re-formulate the OOD problem under the lenses of statistical testing and then discuss conditions that render the OOD problem identifiable in statistical terms. Building on this framework, we study convergence guarantees of an OOD test based on the Wasserstein distance, and provide a simple empirical evaluation.

Structure Learning with Adaptive Random Neighborhood Informed MCMC

In this paper, we introduce a novel MCMC sampler, PARNI-DAG, for a fully-Bayesian approach to the problem of structure learning under observational data. Under the assumption of causal sufficiency, the algorithm allows for approximate sampling directly from the posterior distribution on Directed Acyclic Graphs (DAGs). PARNI-DAG performs efficient sampling of DAGs via locally informed, adaptive random neighborhood proposal that results in better mixing properties. In addition, to ensure better scalability with the number of nodes, we couple PARNI-DAG with a pre-tuning procedure of the sampler's parameters that exploits a skeleton graph derived through some constraint-based or scoring-based algorithms. Thanks to these novel features, PARNI-DAG quickly converges to high-probability regions and is less likely to get stuck in local modes in the presence of high correlation between nodes in high-dimensional settings. After introducing the technical novelties in PARNI-DAG, we empirically demonstrate its mixing efficiency and accuracy in learning DAG structures on a variety of experiments.

Counterfactual Learning with Multioutput Deep Kernels

In this paper, we address the challenge of performing counterfactual inference with observational data via Bayesian nonparametric regression adjustment, with a focus on high-dimensional settings featuring multiple actions and multiple correlated outcomes. We present a general class of counterfactual multi-task deep kernels models that estimate causal effects and learn policies proficiently thanks to their sample efficiency gains, while scaling well with high dimensions. In the first part of the work, we rely on Structural Causal Models (SCM) to formally introduce the setup and the problem of identifying counterfactual quantities under observed confounding. We then discuss the benefits of tackling the task of causal effects estimation via stacked coregionalized Gaussian Processes and Deep Kernels. Finally, we demonstrate the use of the proposed methods on simulated experiments that span individual causal effects estimation, off-policy evaluation and optimization.

Interpretable Deep Causal Learning for Moderation Effects

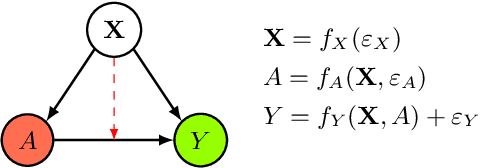
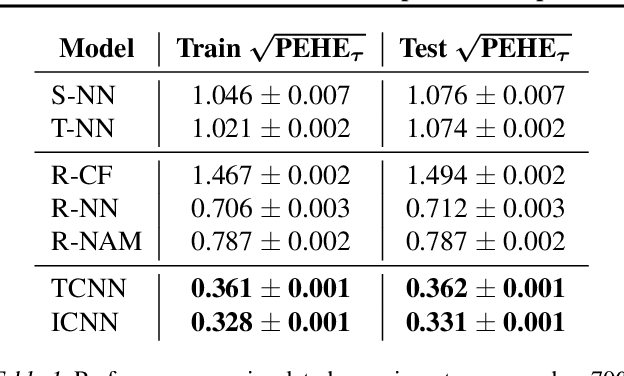
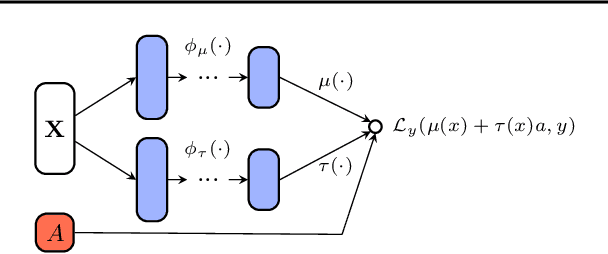
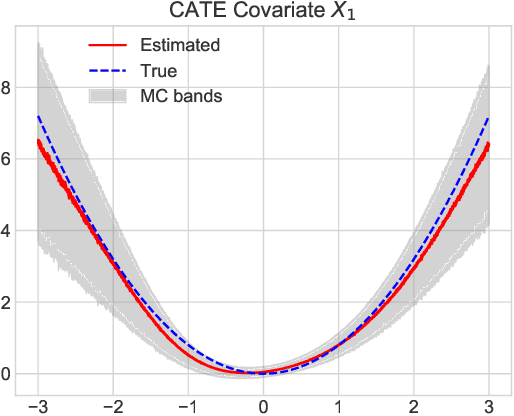
In this extended abstract paper, we address the problem of interpretability and targeted regularization in causal machine learning models. In particular, we focus on the problem of estimating individual causal/treatment effects under observed confounders, which can be controlled for and moderate the effect of the treatment on the outcome of interest. Black-box ML models adjusted for the causal setting perform generally well in this task, but they lack interpretable output identifying the main drivers of treatment heterogeneity and their functional relationship. We propose a novel deep counterfactual learning architecture for estimating individual treatment effects that can simultaneously: i) convey targeted regularization on, and produce quantify uncertainty around the quantity of interest (i.e., the Conditional Average Treatment Effect); ii) disentangle baseline prognostic and moderating effects of the covariates and output interpretable score functions describing their relationship with the outcome. Finally, we demonstrate the use of the method via a simple simulated experiment.

Sparse Bayesian Causal Forests for Heterogeneous Treatment Effects Estimation

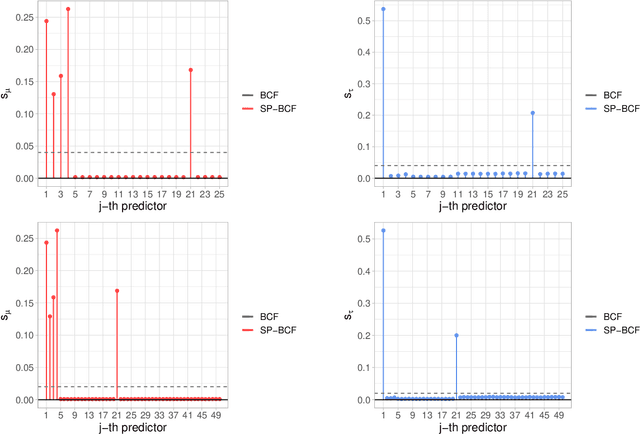
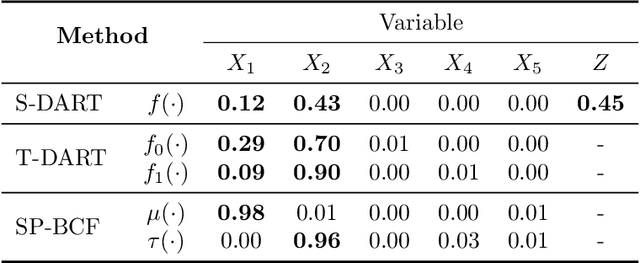
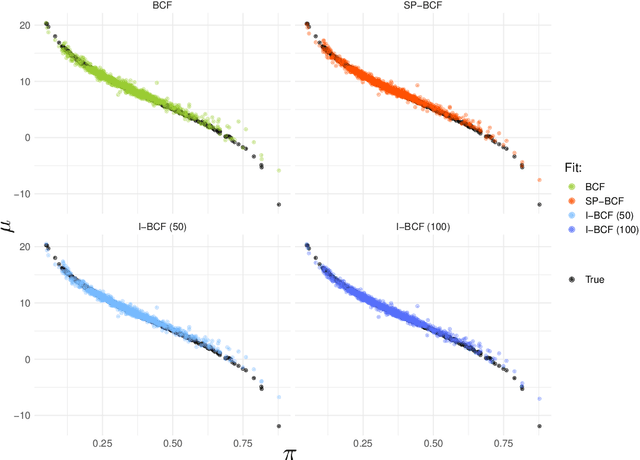
This paper develops a sparsity-inducing version of Bayesian Causal Forests, a recently proposed nonparametric causal regression model that employs Bayesian Additive Regression Trees and is specifically designed to estimate heterogeneous treatment effects using observational data. The sparsity-inducing component we introduce is motivated by empirical studies where the number of pre-treatment covariates available is non-negligible, leading to different degrees of sparsity underlying the surfaces of interest in the estimation of individual treatment effects. The extended version presented in this work, which we name Sparse Bayesian Causal Forest, is equipped with an additional pair of priors allowing the model to adjust the weight of each covariate through the corresponding number of splits in the tree ensemble. These priors improve the model's adaptability to sparse settings and allow to perform fully Bayesian variable selection in a framework for treatment effects estimation, and thus to uncover the moderating factors driving heterogeneity. In addition, the method allows prior knowledge about the relevant confounding pre-treatment covariates and the relative magnitude of their impact on the outcome to be incorporated in the model. We illustrate the performance of our method in simulated studies, in comparison to Bayesian Causal Forest and other state-of-the-art models, to demonstrate how it scales up with an increasing number of covariates and how it handles strongly confounded scenarios. Finally, we also provide an example of application using real-world data.

Estimating Individual Treatment Effects using Non-Parametric Regression Models: a Review

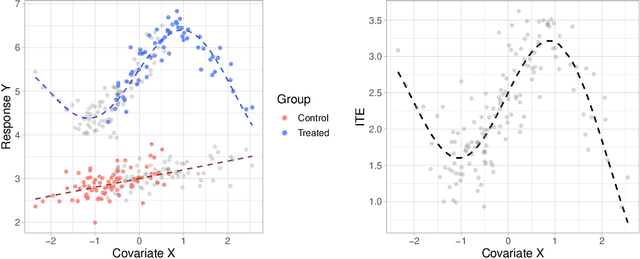
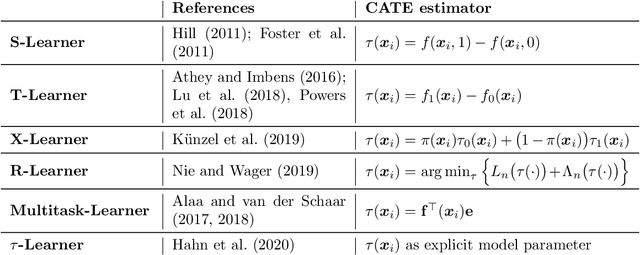
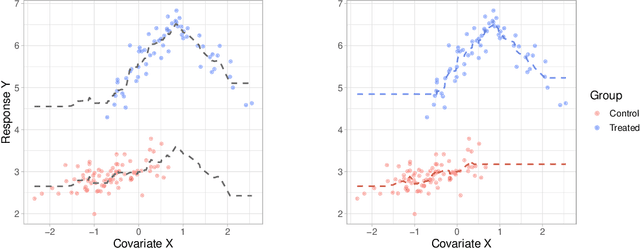
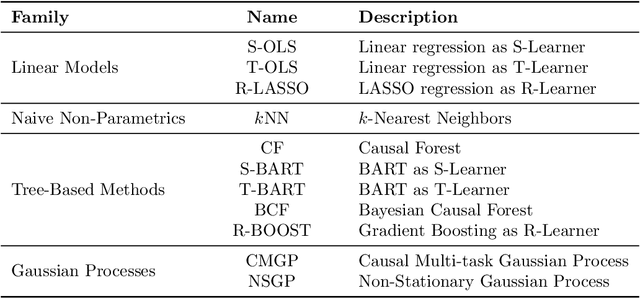
Large observational data are increasingly available in disciplines such as health, economic and social sciences, where researchers are interested in causal questions rather than prediction. In this paper, we investigate the problem of estimating heterogeneous treatment effects using non-parametric regression-based methods. Firstly, we introduce the setup and the issues related to conducting causal inference with observational or non-fully randomized data, and how these issues can be tackled with the help of statistical learning tools. Then, we provide a review of state-of-the-art methods, with a particular focus on non-parametric modeling, and we cast them under a unifying taxonomy. After presenting a brief overview on the problem of model selection, we illustrate the performance of some of the methods on three different simulated studies and on a real world example to investigate the effect of participation in school meal programs on health indicators.