Time-varying Factor Augmented Vector Autoregression with Grouped Sparse Autoencoder

Recent economic events, including the global financial crisis and COVID-19 pandemic, have exposed limitations in linear Factor Augmented Vector Autoregressive (FAVAR) models for forecasting and structural analysis. Nonlinear dimension techniques, particularly autoencoders, have emerged as promising alternatives in a FAVAR framework, but challenges remain in identifiability, interpretability, and integration with traditional nonlinear time series methods. We address these challenges through two contributions. First, we introduce a Grouped Sparse autoencoder that employs the Spike-and-Slab Lasso prior, with parameters under this prior being shared across variables of the same economic category, thereby achieving semi-identifiability and enhancing model interpretability. Second, we incorporate time-varying parameters into the VAR component to better capture evolving economic dynamics. Our empirical application to the US economy demonstrates that the Grouped Sparse autoencoder produces more interpretable factors through its parsimonious structure; and its combination with time-varying parameter VAR shows superior performance in both point and density forecasting. Impulse response analysis reveals that monetary policy shocks during recessions generate more moderate responses with higher uncertainty compared to expansionary periods.

Structure Learning with Adaptive Random Neighborhood Informed MCMC

In this paper, we introduce a novel MCMC sampler, PARNI-DAG, for a fully-Bayesian approach to the problem of structure learning under observational data. Under the assumption of causal sufficiency, the algorithm allows for approximate sampling directly from the posterior distribution on Directed Acyclic Graphs (DAGs). PARNI-DAG performs efficient sampling of DAGs via locally informed, adaptive random neighborhood proposal that results in better mixing properties. In addition, to ensure better scalability with the number of nodes, we couple PARNI-DAG with a pre-tuning procedure of the sampler's parameters that exploits a skeleton graph derived through some constraint-based or scoring-based algorithms. Thanks to these novel features, PARNI-DAG quickly converges to high-probability regions and is less likely to get stuck in local modes in the presence of high correlation between nodes in high-dimensional settings. After introducing the technical novelties in PARNI-DAG, we empirically demonstrate its mixing efficiency and accuracy in learning DAG structures on a variety of experiments.

Modelling and computation using NCoRM mixtures for density regression

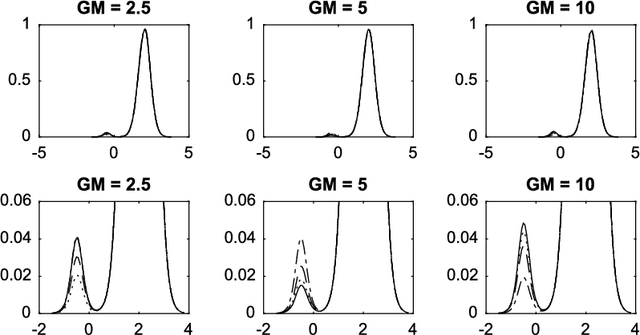
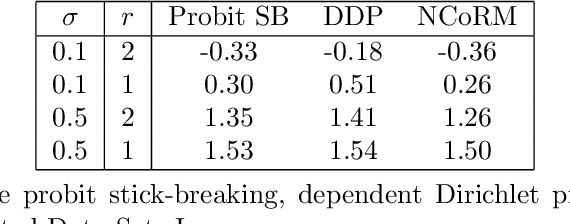
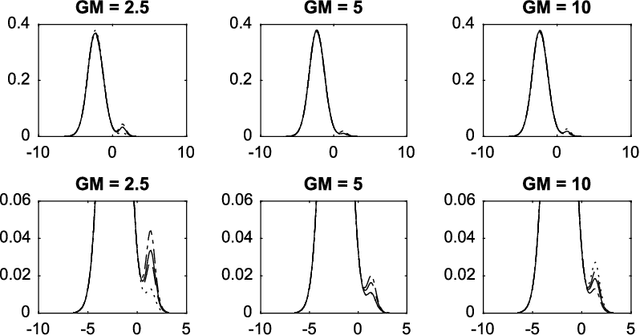
Normalized compound random measures are flexible nonparametric priors for related distributions. We consider building general nonparametric regression models using normalized compound random measure mixture models. Posterior inference is made using a novel pseudo-marginal Metropolis-Hastings sampler for normalized compound random measure mixture models. The algorithm makes use of a new general approach to the unbiased estimation of Laplace functionals of compound random measures (which includes completely random measures as a special case). The approach is illustrated on problems of density regression.