Modelling Preference Data with the Wallenius Distribution

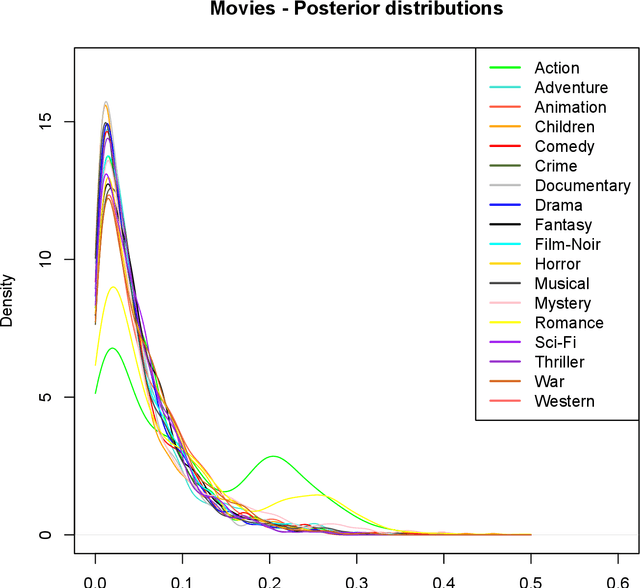
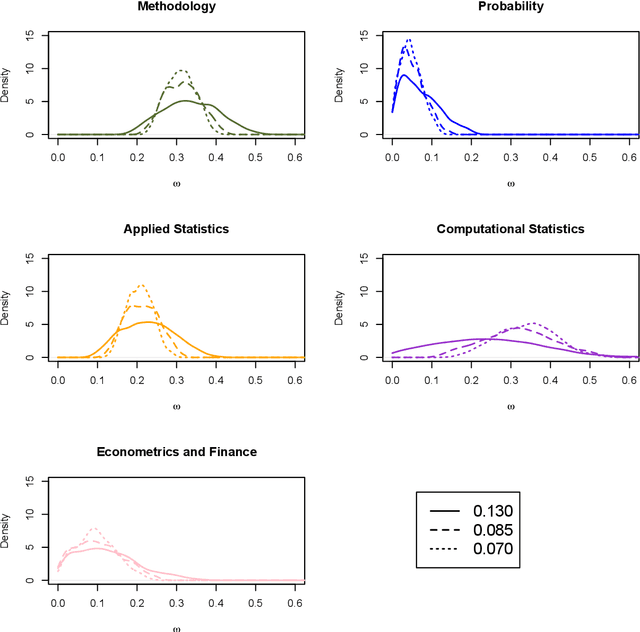
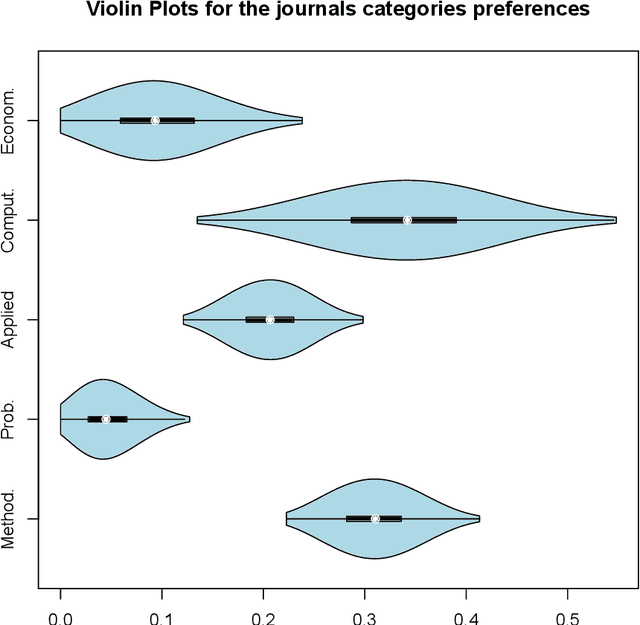
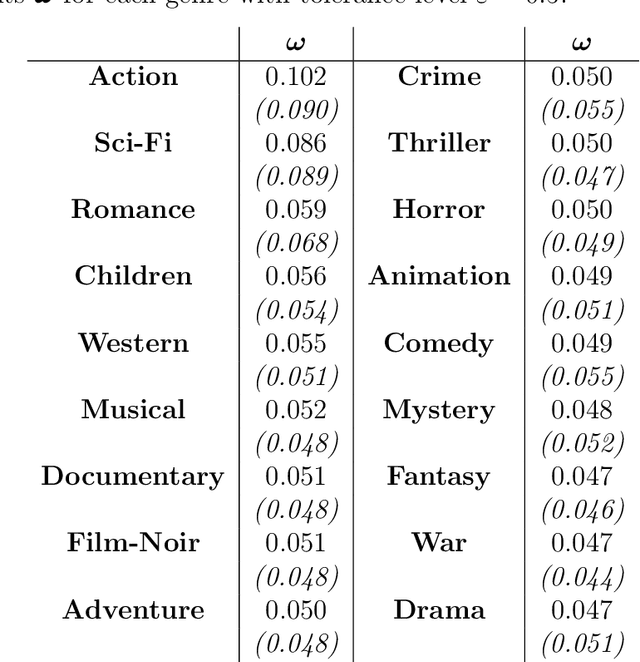
The Wallenius distribution is a generalisation of the Hypergeometric distribution where weights are assigned to balls of different colours. This naturally defines a model for ranking categories which can be used for classification purposes. Since, in general, the resulting likelihood is not analytically available, we adopt an approximate Bayesian computational (ABC) approach for estimating the importance of the categories. We illustrate the performance of the estimation procedure on simulated datasets. Finally, we use the new model for analysing two datasets about movies ratings and Italian academic statisticians' journal preferences. The latter is a novel dataset collected by the authors.

Objective Bayesian Analysis for Change Point Problems

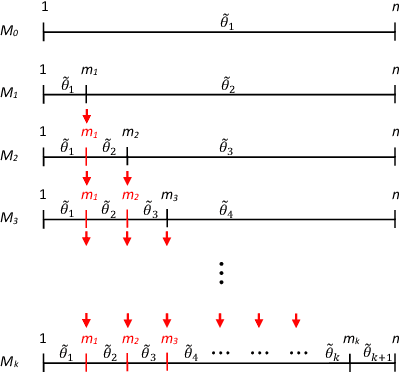
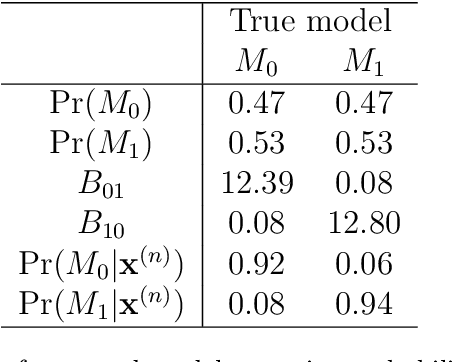
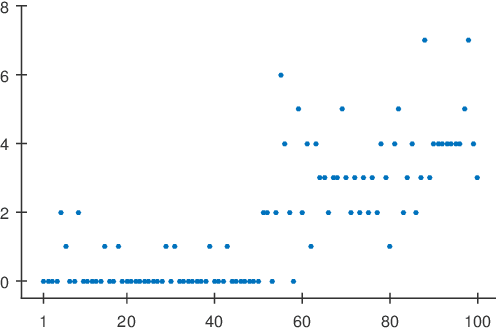
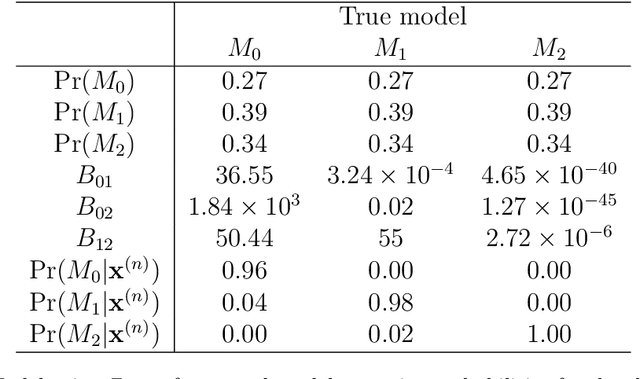
In this paper we present a loss-based approach to change point analysis. In particular, we look at the problem from two perspectives. The first focuses on the definition of a prior when the number of change points is known a priori. The second contribution aims to estimate the number of change points by using a loss-based approach recently introduced in the literature. The latter considers change point estimation as a model selection exercise. We show the performance of the proposed approach on simulated data and real data sets.

Modelling and computation using NCoRM mixtures for density regression

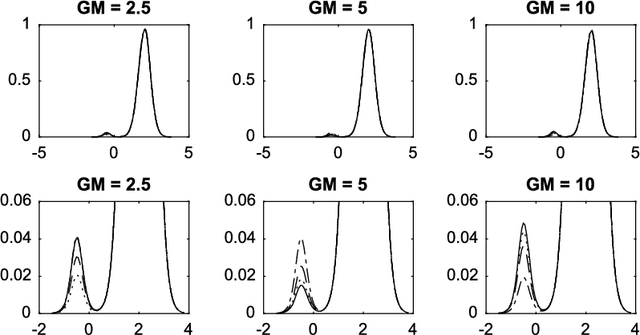
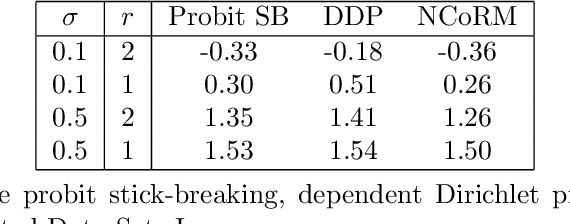
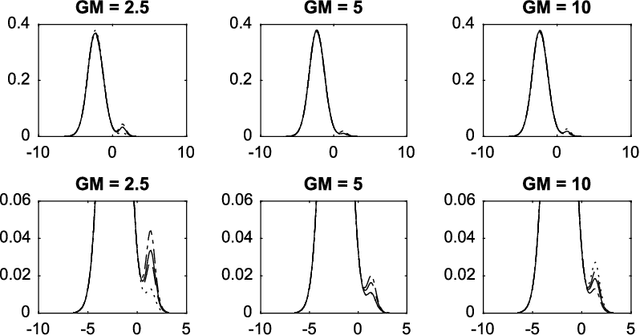
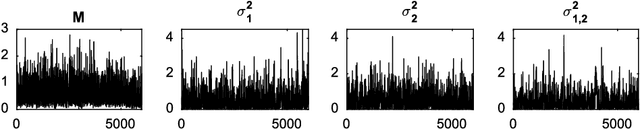
Normalized compound random measures are flexible nonparametric priors for related distributions. We consider building general nonparametric regression models using normalized compound random measure mixture models. Posterior inference is made using a novel pseudo-marginal Metropolis-Hastings sampler for normalized compound random measure mixture models. The algorithm makes use of a new general approach to the unbiased estimation of Laplace functionals of compound random measures (which includes completely random measures as a special case). The approach is illustrated on problems of density regression.

Generalized Species Sampling Priors with Latent Beta reinforcements

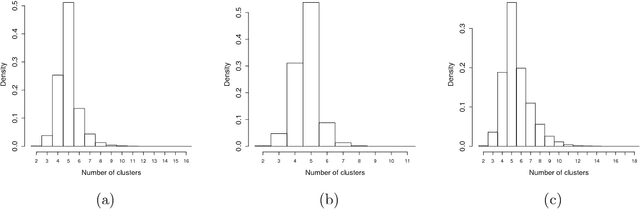
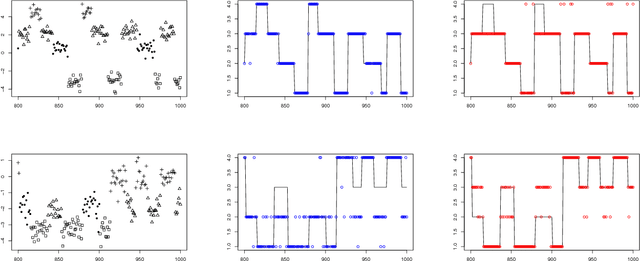
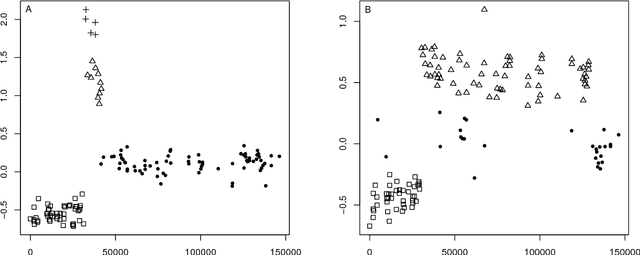
Many popular Bayesian nonparametric priors can be characterized in terms of exchangeable species sampling sequences. However, in some applications, exchangeability may not be appropriate. We introduce a {novel and probabilistically coherent family of non-exchangeable species sampling sequences characterized by a tractable predictive probability function with weights driven by a sequence of independent Beta random variables. We compare their theoretical clustering properties with those of the Dirichlet Process and the two parameters Poisson-Dirichlet process. The proposed construction provides a complete characterization of the joint process, differently from existing work. We then propose the use of such process as prior distribution in a hierarchical Bayes modeling framework, and we describe a Markov Chain Monte Carlo sampler for posterior inference. We evaluate the performance of the prior and the robustness of the resulting inference in a simulation study, providing a comparison with popular Dirichlet Processes mixtures and Hidden Markov Models. Finally, we develop an application to the detection of chromosomal aberrations in breast cancer by leveraging array CGH data.