Feature learning in finite-width Bayesian deep linear networks with multiple outputs and convolutional layers

Deep linear networks have been extensively studied, as they provide simplified models of deep learning. However, little is known in the case of finite-width architectures with multiple outputs and convolutional layers. In this manuscript, we provide rigorous results for the statistics of functions implemented by the aforementioned class of networks, thus moving closer to a complete characterization of feature learning in the Bayesian setting. Our results include: (i) an exact and elementary non-asymptotic integral representation for the joint prior distribution over the outputs, given in terms of a mixture of Gaussians; (ii) an analytical formula for the posterior distribution in the case of squared error loss function (Gaussian likelihood); (iii) a quantitative description of the feature learning infinite-width regime, using large deviation theory. From a physical perspective, deep architectures with multiple outputs or convolutional layers represent different manifestations of kernel shape renormalization, and our work provides a dictionary that translates this physics intuition and terminology into rigorous Bayesian statistics.

Computing Kantorovich-Wasserstein Distances on $d$-dimensional histograms using $(d+1)$-partite graphs

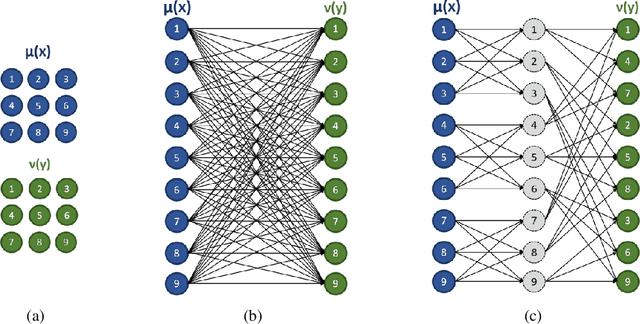
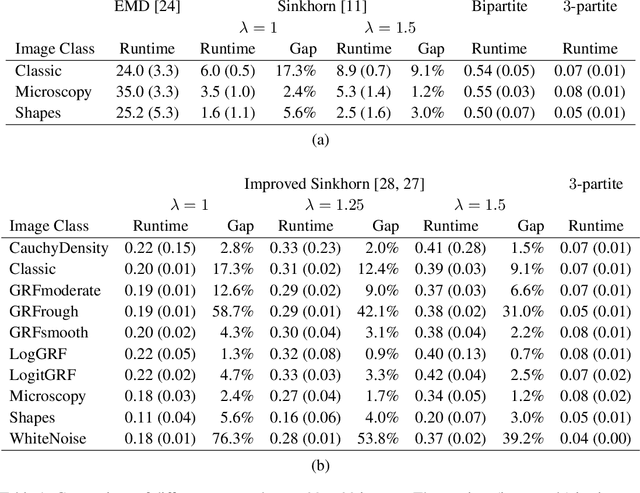
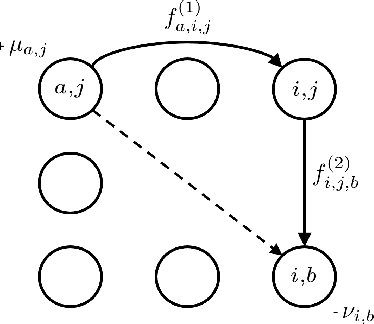
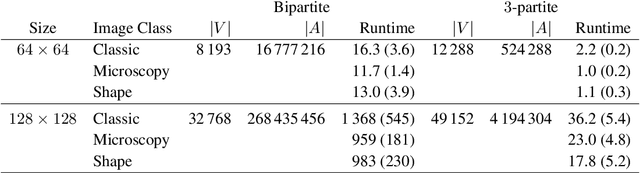
This paper presents a novel method to compute the exact Kantorovich-Wasserstein distance between a pair of $d$-dimensional histograms having $n$ bins each. We prove that this problem is equivalent to an uncapacitated minimum cost flow problem on a $(d+1)$-partite graph with $(d+1)n$ nodes and $dn^{\frac{d+1}{d}}$ arcs, whenever the cost is separable along the principal $d$-dimensional directions. We show numerically the benefits of our approach by computing the Kantorovich-Wasserstein distance of order 2 among two sets of instances: gray scale images and $d$-dimensional biomedical histograms. On these types of instances, our approach is competitive with state-of-the-art optimal transport algorithms.

On the Computation of Kantorovich-Wasserstein Distances between 2D-Histograms by Uncapacitated Minimum Cost Flows

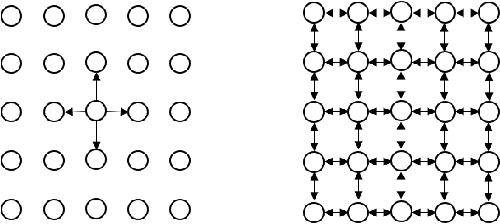
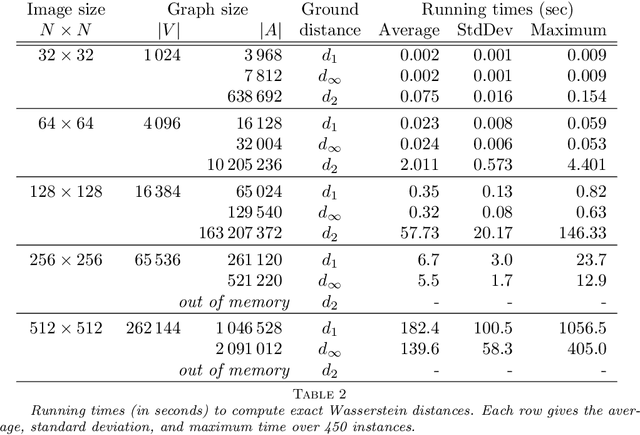
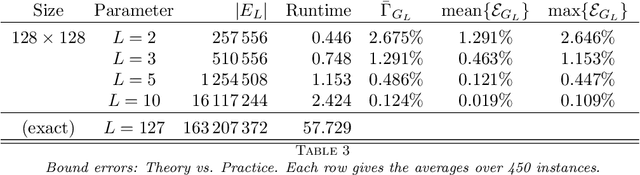
In this work, we present a method to compute the Kantorovich distance, that is, the Wasserstein distance of order one, between a pair of two-dimensional histograms. Recent works in Computer Vision and Machine Learning have shown the benefits of measuring Wasserstein distances of order one between histograms with $N$ bins, by solving a classical transportation problem on (very large) complete bipartite graphs with $N$ nodes and $N^2$ edges. The main contribution of our work is to approximate the original transportation problem by an uncapacitated min cost flow problem on a reduced flow network of size $O(N)$. More precisely, when the distance among the bin centers is measured with the 1-norm or the $\infty$-norm, our approach provides an optimal solution. When the distance amongst bins is measured with the 2-norm: (i) we derive a quantitative estimate on the error between optimal and approximate solution; (ii) given the error, we construct a reduced flow network of size $O(N)$. We numerically show the benefits of our approach by computing Wasserstein distances of order one on a set of grey scale images used as benchmarks in the literature. We show how our approach scales with the size of the images with 1-norm, 2-norm and $\infty$-norm ground distances.

Generalized Species Sampling Priors with Latent Beta reinforcements

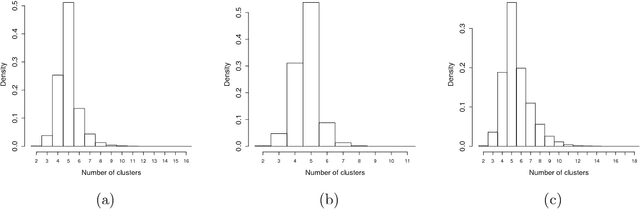
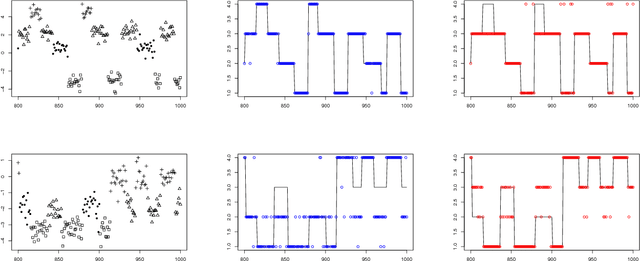
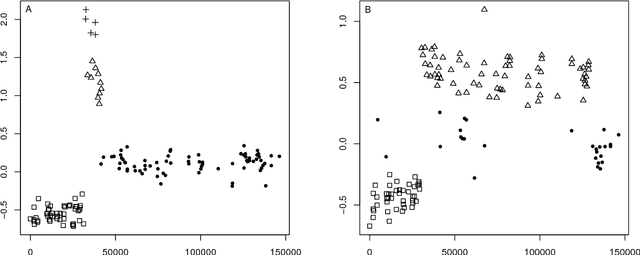
Many popular Bayesian nonparametric priors can be characterized in terms of exchangeable species sampling sequences. However, in some applications, exchangeability may not be appropriate. We introduce a {novel and probabilistically coherent family of non-exchangeable species sampling sequences characterized by a tractable predictive probability function with weights driven by a sequence of independent Beta random variables. We compare their theoretical clustering properties with those of the Dirichlet Process and the two parameters Poisson-Dirichlet process. The proposed construction provides a complete characterization of the joint process, differently from existing work. We then propose the use of such process as prior distribution in a hierarchical Bayes modeling framework, and we describe a Markov Chain Monte Carlo sampler for posterior inference. We evaluate the performance of the prior and the robustness of the resulting inference in a simulation study, providing a comparison with popular Dirichlet Processes mixtures and Hidden Markov Models. Finally, we develop an application to the detection of chromosomal aberrations in breast cancer by leveraging array CGH data.