From Kinetic Theory to AI: a Rediscovery of High-Dimensional Divergences and Their Properties

Selecting an appropriate divergence measure is a critical aspect of machine learning, as it directly impacts model performance. Among the most widely used, we find the Kullback-Leibler (KL) divergence, originally introduced in kinetic theory as a measure of relative entropy between probability distributions. Just as in machine learning, the ability to quantify the proximity of probability distributions plays a central role in kinetic theory. In this paper, we present a comparative review of divergence measures rooted in kinetic theory, highlighting their theoretical foundations and exploring their potential applications in machine learning and artificial intelligence.

The Equivalence of Fourier-based and Wasserstein Metrics on Imaging Problems

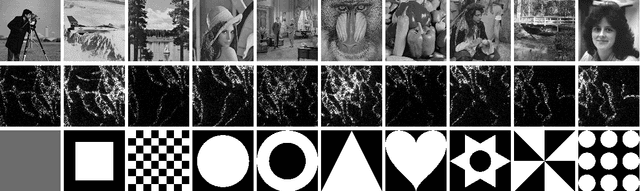
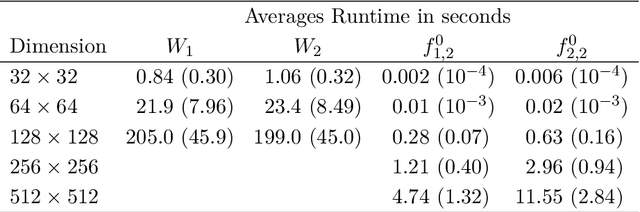
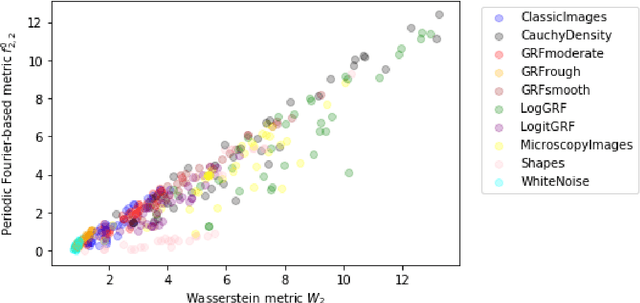
We investigate properties of some extensions of a class of Fourier-based probability metrics, originally introduced to study convergence to equilibrium for the solution to the spatially homogeneous Boltzmann equation. At difference with the original one, the new Fourier-based metrics are well-defined also for probability distributions with different centers of mass, and for discrete probability measures supported over a regular grid. Among other properties, it is shown that, in the discrete setting, these new Fourier-based metrics are equivalent either to the Euclidean-Wasserstein distance $W_2$, or to the Kantorovich-Wasserstein distance $W_1$, with explicit constants of equivalence. Numerical results then show that in benchmark problems of image processing, Fourier metrics provide a better runtime with respect to Wasserstein ones.

Computing Kantorovich-Wasserstein Distances on $d$-dimensional histograms using $(d+1)$-partite graphs

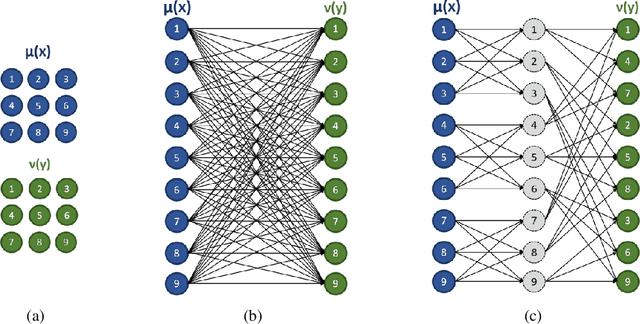
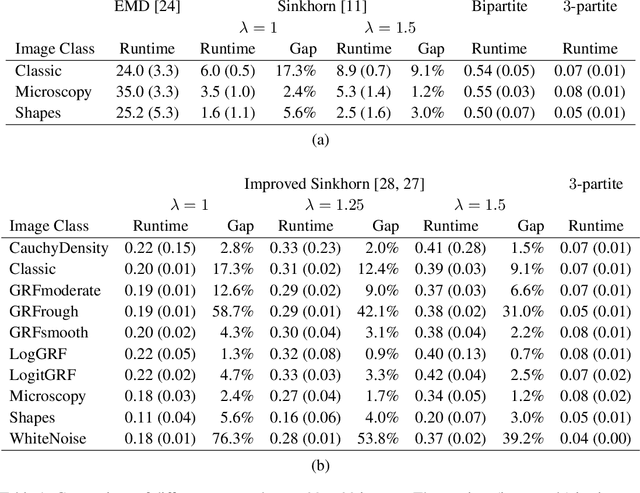
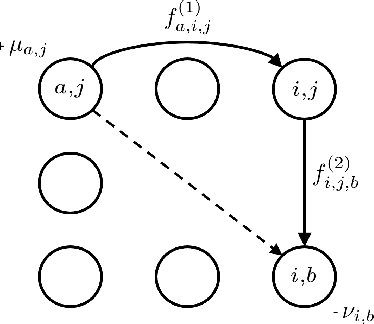
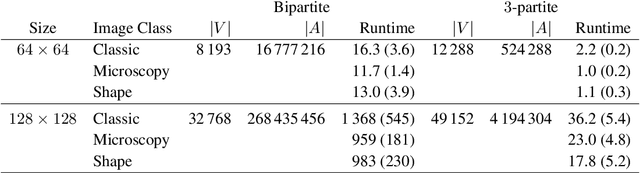
This paper presents a novel method to compute the exact Kantorovich-Wasserstein distance between a pair of $d$-dimensional histograms having $n$ bins each. We prove that this problem is equivalent to an uncapacitated minimum cost flow problem on a $(d+1)$-partite graph with $(d+1)n$ nodes and $dn^{\frac{d+1}{d}}$ arcs, whenever the cost is separable along the principal $d$-dimensional directions. We show numerically the benefits of our approach by computing the Kantorovich-Wasserstein distance of order 2 among two sets of instances: gray scale images and $d$-dimensional biomedical histograms. On these types of instances, our approach is competitive with state-of-the-art optimal transport algorithms.