The Equivalence of Fourier-based and Wasserstein Metrics on Imaging Problems

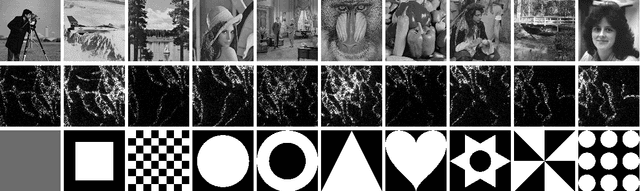
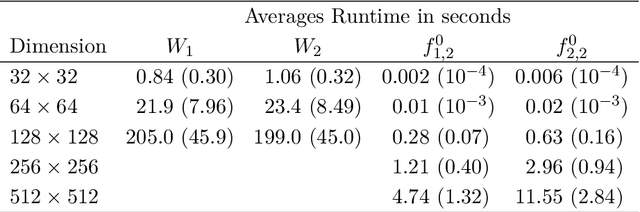
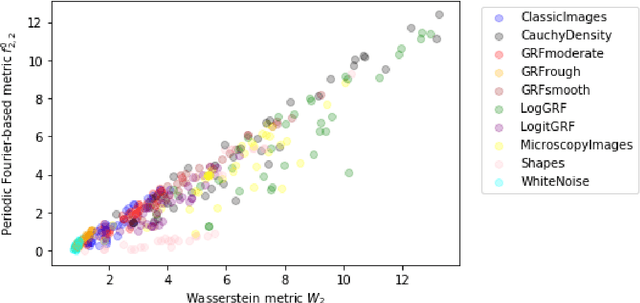
We investigate properties of some extensions of a class of Fourier-based probability metrics, originally introduced to study convergence to equilibrium for the solution to the spatially homogeneous Boltzmann equation. At difference with the original one, the new Fourier-based metrics are well-defined also for probability distributions with different centers of mass, and for discrete probability measures supported over a regular grid. Among other properties, it is shown that, in the discrete setting, these new Fourier-based metrics are equivalent either to the Euclidean-Wasserstein distance $W_2$, or to the Kantorovich-Wasserstein distance $W_1$, with explicit constants of equivalence. Numerical results then show that in benchmark problems of image processing, Fourier metrics provide a better runtime with respect to Wasserstein ones.

Computing Kantorovich-Wasserstein Distances on $d$-dimensional histograms using $(d+1)$-partite graphs

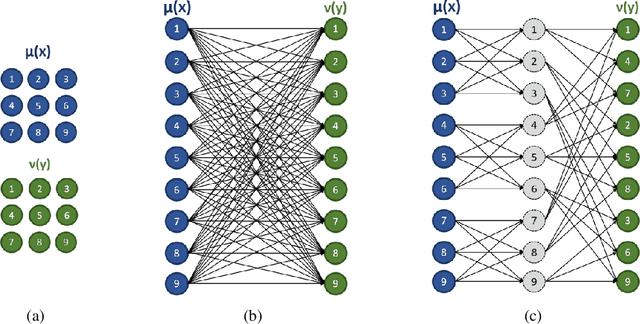
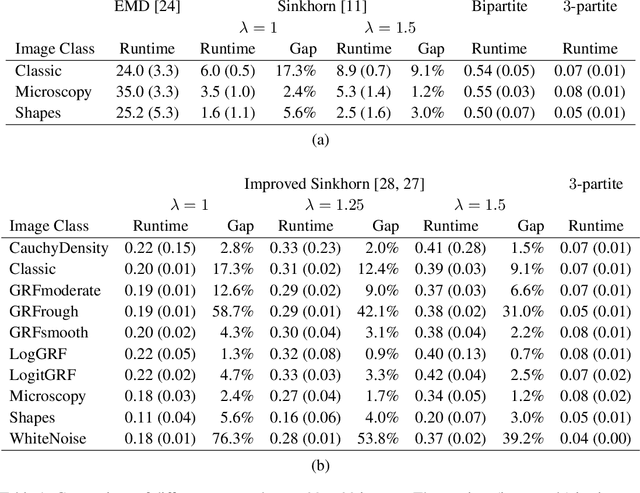
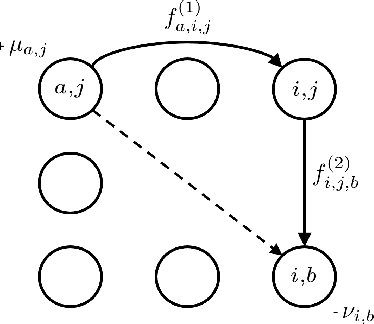
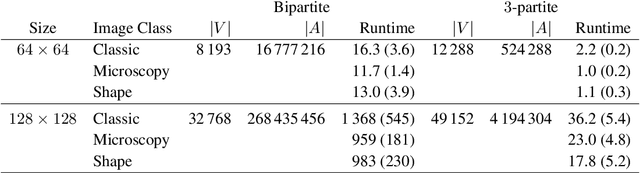
This paper presents a novel method to compute the exact Kantorovich-Wasserstein distance between a pair of $d$-dimensional histograms having $n$ bins each. We prove that this problem is equivalent to an uncapacitated minimum cost flow problem on a $(d+1)$-partite graph with $(d+1)n$ nodes and $dn^{\frac{d+1}{d}}$ arcs, whenever the cost is separable along the principal $d$-dimensional directions. We show numerically the benefits of our approach by computing the Kantorovich-Wasserstein distance of order 2 among two sets of instances: gray scale images and $d$-dimensional biomedical histograms. On these types of instances, our approach is competitive with state-of-the-art optimal transport algorithms.

On the Computation of Kantorovich-Wasserstein Distances between 2D-Histograms by Uncapacitated Minimum Cost Flows

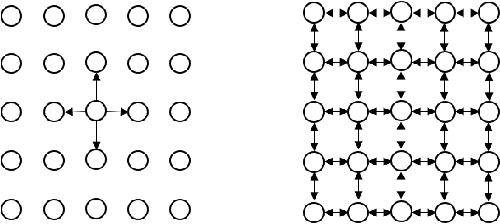
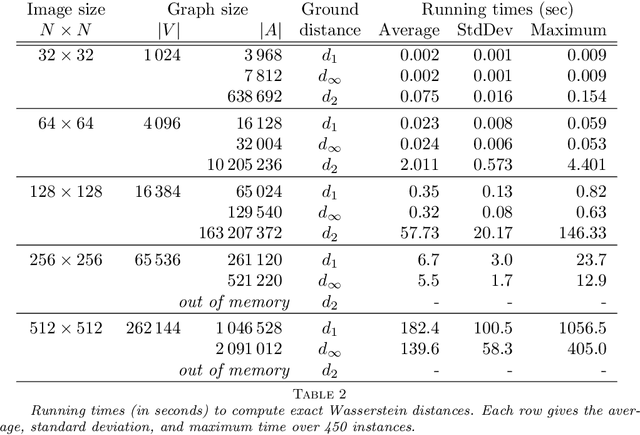
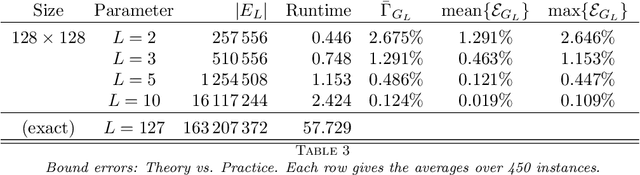
In this work, we present a method to compute the Kantorovich distance, that is, the Wasserstein distance of order one, between a pair of two-dimensional histograms. Recent works in Computer Vision and Machine Learning have shown the benefits of measuring Wasserstein distances of order one between histograms with $N$ bins, by solving a classical transportation problem on (very large) complete bipartite graphs with $N$ nodes and $N^2$ edges. The main contribution of our work is to approximate the original transportation problem by an uncapacitated min cost flow problem on a reduced flow network of size $O(N)$. More precisely, when the distance among the bin centers is measured with the 1-norm or the $\infty$-norm, our approach provides an optimal solution. When the distance amongst bins is measured with the 2-norm: (i) we derive a quantitative estimate on the error between optimal and approximate solution; (ii) given the error, we construct a reduced flow network of size $O(N)$. We numerically show the benefits of our approach by computing Wasserstein distances of order one on a set of grey scale images used as benchmarks in the literature. We show how our approach scales with the size of the images with 1-norm, 2-norm and $\infty$-norm ground distances.