Computing Kantorovich-Wasserstein Distances on $d$-dimensional histograms using $(d+1)$-partite graphs
Paper and Code
May 18, 2018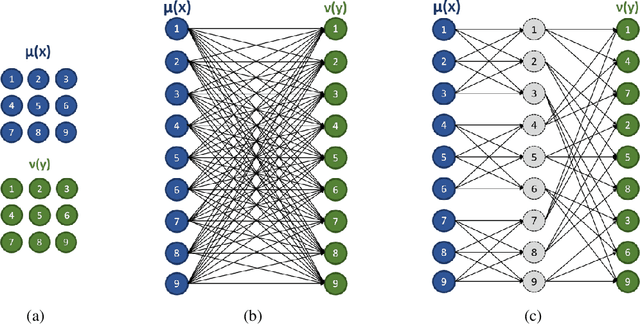
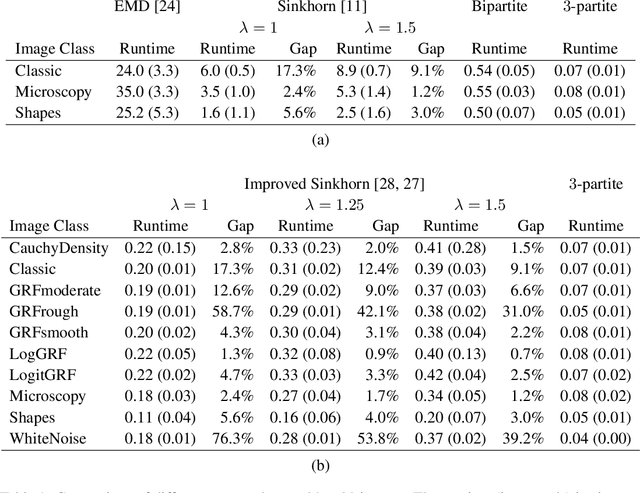
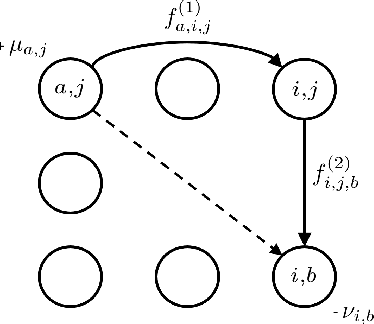
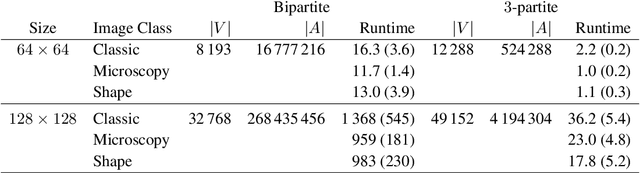
This paper presents a novel method to compute the exact Kantorovich-Wasserstein distance between a pair of $d$-dimensional histograms having $n$ bins each. We prove that this problem is equivalent to an uncapacitated minimum cost flow problem on a $(d+1)$-partite graph with $(d+1)n$ nodes and $dn^{\frac{d+1}{d}}$ arcs, whenever the cost is separable along the principal $d$-dimensional directions. We show numerically the benefits of our approach by computing the Kantorovich-Wasserstein distance of order 2 among two sets of instances: gray scale images and $d$-dimensional biomedical histograms. On these types of instances, our approach is competitive with state-of-the-art optimal transport algorithms.
* 12 pages, 3 figures, 3 tables
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge