The BeMi Stardust: a Structured Ensemble of Binarized Neural Networks

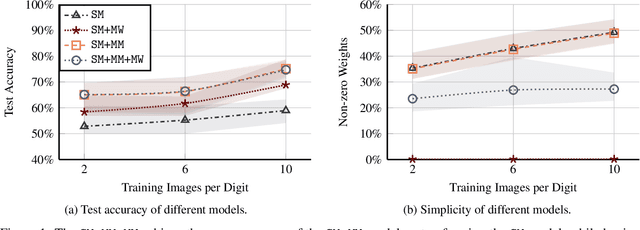
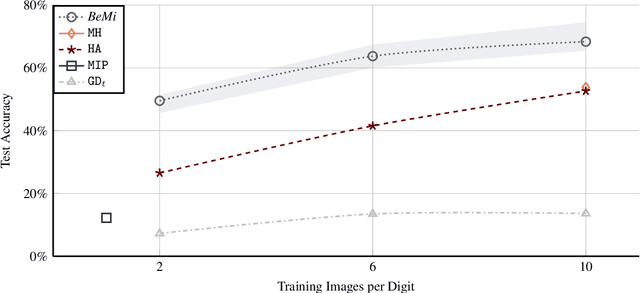
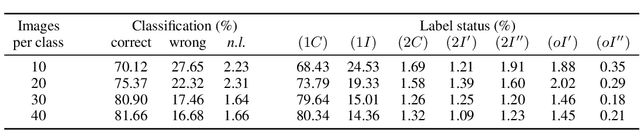
Binarized Neural Networks (BNNs) are receiving increasing attention due to their lightweight architecture and ability to run on low-power devices. The state-of-the-art for training classification BNNs restricted to few-shot learning is based on a Mixed Integer Programming (MIP) approach. This paper proposes the BeMi ensemble, a structured architecture of BNNs based on training a single BNN for each possible pair of classes and applying a majority voting scheme to predict the final output. The training of a single BNN discriminating between two classes is achieved by a MIP model that optimizes a lexicographic multi-objective function according to robustness and simplicity principles. This approach results in training networks whose output is not affected by small perturbations on the input and whose number of active weights is as small as possible, while good accuracy is preserved. We computationally validate our model using the MNIST and Fashion-MNIST datasets using up to 40 training images per class. Our structured ensemble outperforms both BNNs trained by stochastic gradient descent and state-of-the-art MIP-based approaches. While the previous approaches achieve an average accuracy of 51.1% on the MNIST dataset, the BeMi ensemble achieves an average accuracy of 61.7% when trained with 10 images per class and 76.4% when trained with 40 images per class.

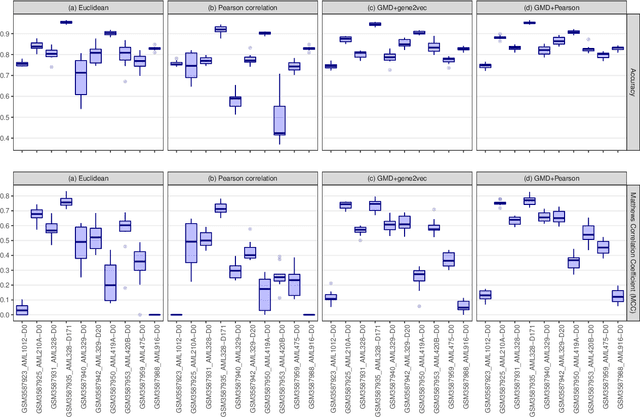
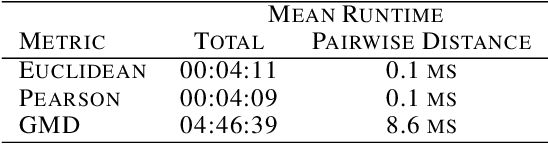
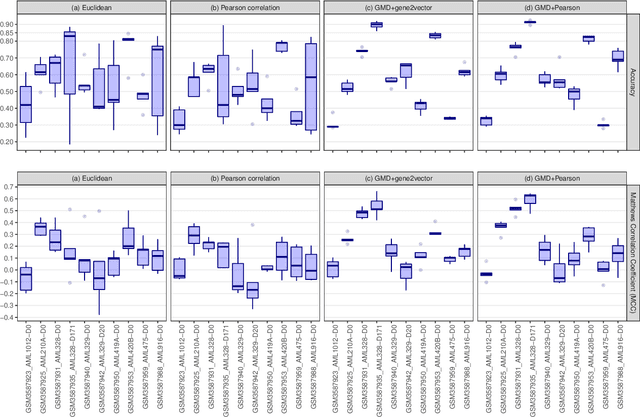
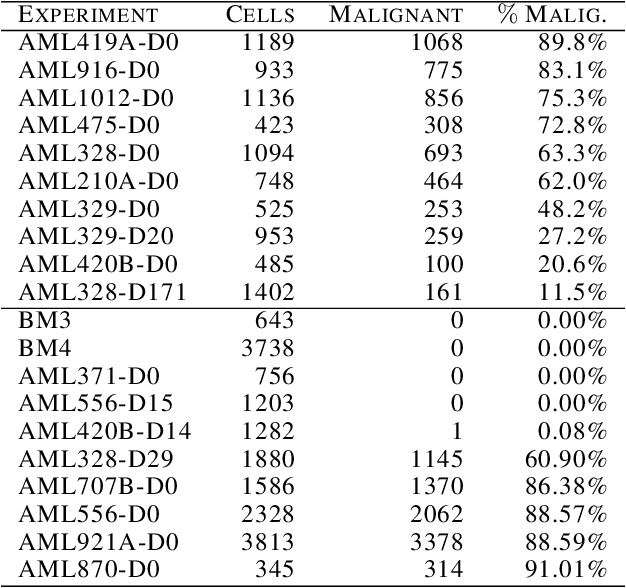
The Gene Mover's Distance: Single-cell similarity via Optimal Transport

This paper introduces the Gene Mover's Distance, a measure of similarity between a pair of cells based on their gene expression profiles obtained via single-cell RNA sequencing. The underlying idea of the proposed distance is to interpret the gene expression array of a single cell as a discrete probability measure. The distance between two cells is hence computed by solving an Optimal Transport problem between the two corresponding discrete measures. In the Optimal Transport model, we use two types of cost function for measuring the distance between a pair of genes. The first cost function exploits a gene embedding, called gene2vec, which is used to map each gene to a high dimensional vector: the cost of moving a unit of mass of gene expression from a gene to another is set to the Euclidean distance between the corresponding embedded vectors. The second cost function is based on a Pearson distance among pairs of genes. In both cost functions, the more two genes are correlated, the lower is their distance. We exploit the Gene Mover's Distance to solve two classification problems: the classification of cells according to their condition and according to their type. To assess the impact of our new metric, we compare the performances of a $k$-Nearest Neighbor classifier using different distances. The computational results show that the Gene Mover's Distance is competitive with the state-of-the-art distances used in the literature.

The Equivalence of Fourier-based and Wasserstein Metrics on Imaging Problems

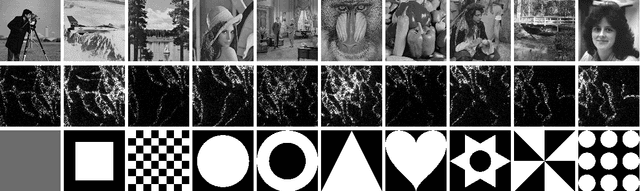
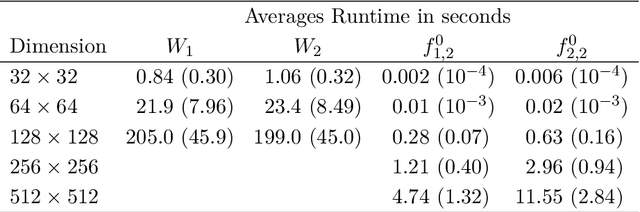
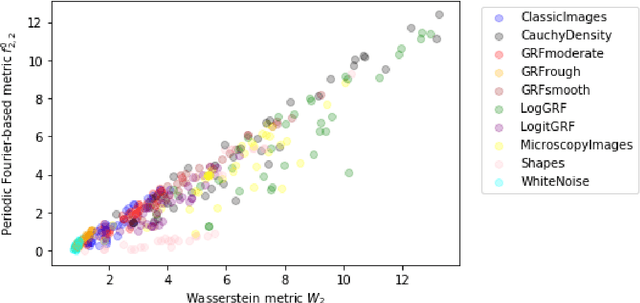
We investigate properties of some extensions of a class of Fourier-based probability metrics, originally introduced to study convergence to equilibrium for the solution to the spatially homogeneous Boltzmann equation. At difference with the original one, the new Fourier-based metrics are well-defined also for probability distributions with different centers of mass, and for discrete probability measures supported over a regular grid. Among other properties, it is shown that, in the discrete setting, these new Fourier-based metrics are equivalent either to the Euclidean-Wasserstein distance $W_2$, or to the Kantorovich-Wasserstein distance $W_1$, with explicit constants of equivalence. Numerical results then show that in benchmark problems of image processing, Fourier metrics provide a better runtime with respect to Wasserstein ones.

Computing Kantorovich-Wasserstein Distances on $d$-dimensional histograms using $(d+1)$-partite graphs

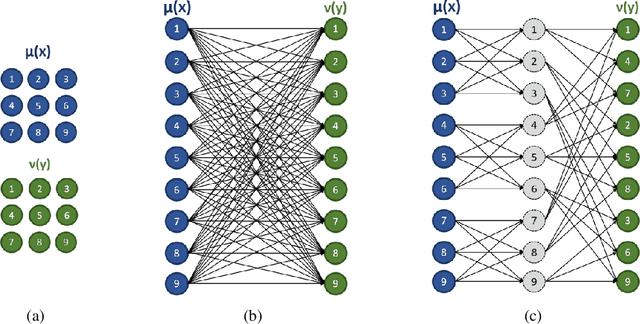
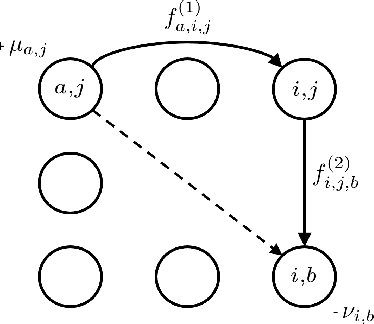
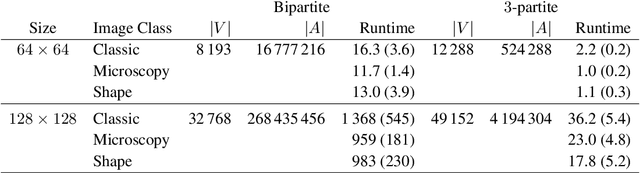
This paper presents a novel method to compute the exact Kantorovich-Wasserstein distance between a pair of $d$-dimensional histograms having $n$ bins each. We prove that this problem is equivalent to an uncapacitated minimum cost flow problem on a $(d+1)$-partite graph with $(d+1)n$ nodes and $dn^{\frac{d+1}{d}}$ arcs, whenever the cost is separable along the principal $d$-dimensional directions. We show numerically the benefits of our approach by computing the Kantorovich-Wasserstein distance of order 2 among two sets of instances: gray scale images and $d$-dimensional biomedical histograms. On these types of instances, our approach is competitive with state-of-the-art optimal transport algorithms.

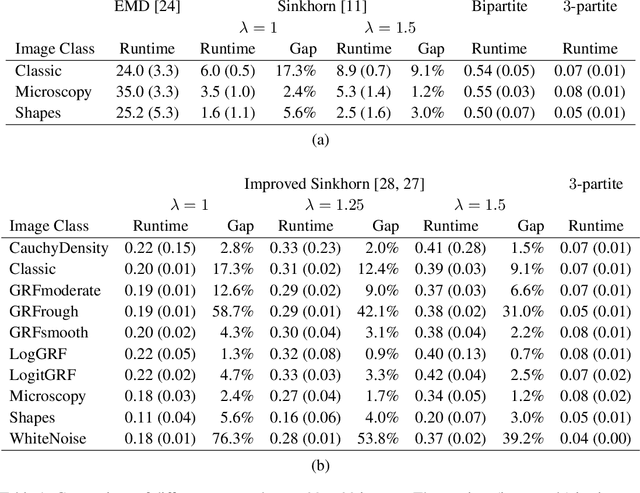
On the Computation of Kantorovich-Wasserstein Distances between 2D-Histograms by Uncapacitated Minimum Cost Flows

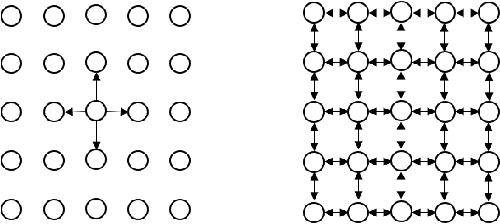
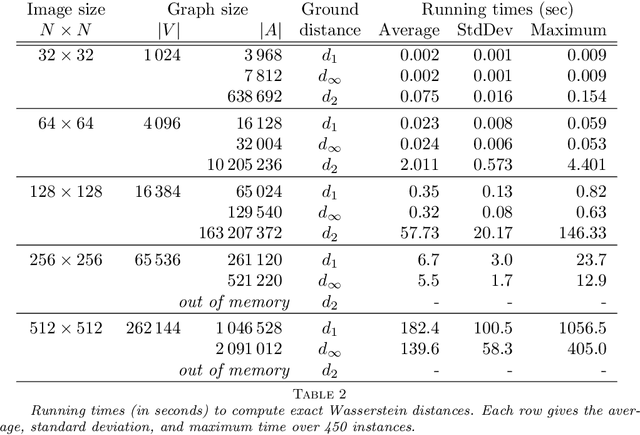
In this work, we present a method to compute the Kantorovich distance, that is, the Wasserstein distance of order one, between a pair of two-dimensional histograms. Recent works in Computer Vision and Machine Learning have shown the benefits of measuring Wasserstein distances of order one between histograms with $N$ bins, by solving a classical transportation problem on (very large) complete bipartite graphs with $N$ nodes and $N^2$ edges. The main contribution of our work is to approximate the original transportation problem by an uncapacitated min cost flow problem on a reduced flow network of size $O(N)$. More precisely, when the distance among the bin centers is measured with the 1-norm or the $\infty$-norm, our approach provides an optimal solution. When the distance amongst bins is measured with the 2-norm: (i) we derive a quantitative estimate on the error between optimal and approximate solution; (ii) given the error, we construct a reduced flow network of size $O(N)$. We numerically show the benefits of our approach by computing Wasserstein distances of order one on a set of grey scale images used as benchmarks in the literature. We show how our approach scales with the size of the images with 1-norm, 2-norm and $\infty$-norm ground distances.