TSP with Predictions: Heatmap to Tour with Provable Guarantees

The Traveling Salesperson Problem (TSP) has long served as a benchmark for evaluating the strength of optimization techniques in the classical theory of algorithms. In recent efforts to apply ML to algorithmic problems, TSP has also become a natural testbed for the development of ML-based techniques. A common approach is to train a neural network to output a heatmap estimating the likelihood of each edge to be part of the optimal tour; however, converting such a heatmap into an actual tour remains a non-trivial and often computationally intensive step. In this work, we propose algorithms for transforming heatmaps into tours with theoretical guarantees linking the achieved approximation ratio to the quality of the provided heatmap. In the spirit of algorithms with predictions, our results can be described as $(1+2\fracη{\mathrm{OPT}})$-approximation algorithms, where $η$ denotes the L1 distance between the prediction (heatmap) and an optimal solution (tour). Since the previous works lack such explicit guarantees, we compare our approach against them experimentally.

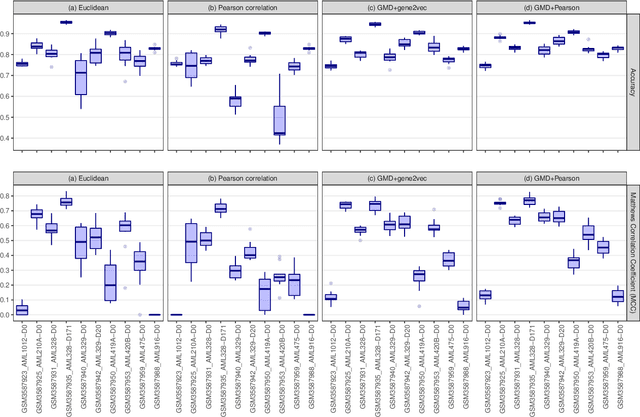
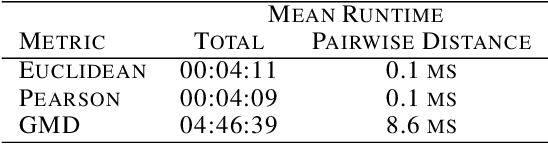
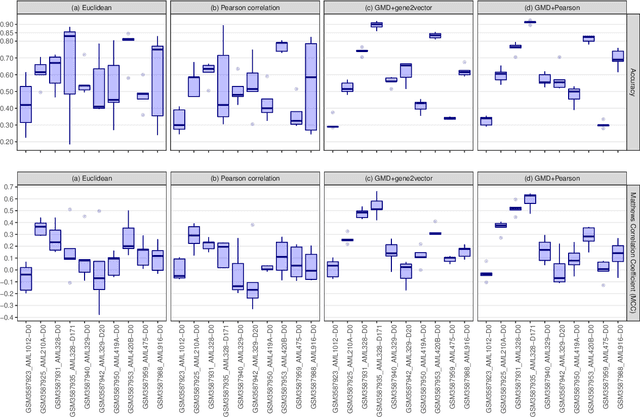
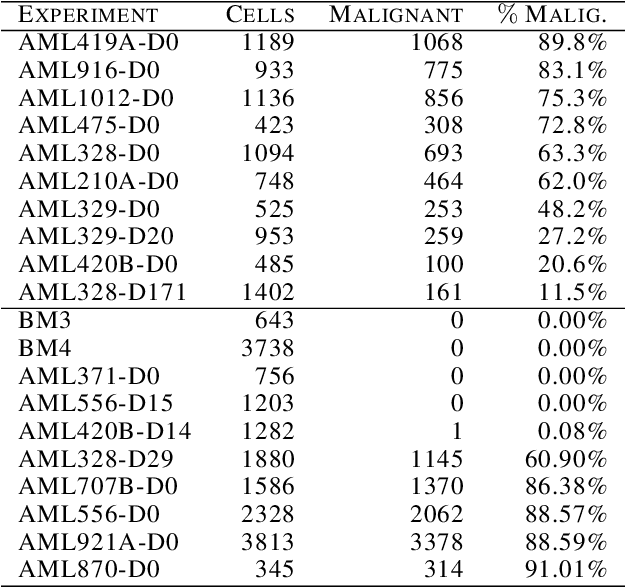
The Gene Mover's Distance: Single-cell similarity via Optimal Transport

This paper introduces the Gene Mover's Distance, a measure of similarity between a pair of cells based on their gene expression profiles obtained via single-cell RNA sequencing. The underlying idea of the proposed distance is to interpret the gene expression array of a single cell as a discrete probability measure. The distance between two cells is hence computed by solving an Optimal Transport problem between the two corresponding discrete measures. In the Optimal Transport model, we use two types of cost function for measuring the distance between a pair of genes. The first cost function exploits a gene embedding, called gene2vec, which is used to map each gene to a high dimensional vector: the cost of moving a unit of mass of gene expression from a gene to another is set to the Euclidean distance between the corresponding embedded vectors. The second cost function is based on a Pearson distance among pairs of genes. In both cost functions, the more two genes are correlated, the lower is their distance. We exploit the Gene Mover's Distance to solve two classification problems: the classification of cells according to their condition and according to their type. To assess the impact of our new metric, we compare the performances of a $k$-Nearest Neighbor classifier using different distances. The computational results show that the Gene Mover's Distance is competitive with the state-of-the-art distances used in the literature.