On the Computation of Kantorovich-Wasserstein Distances between 2D-Histograms by Uncapacitated Minimum Cost Flows
Paper and Code
Apr 04, 2018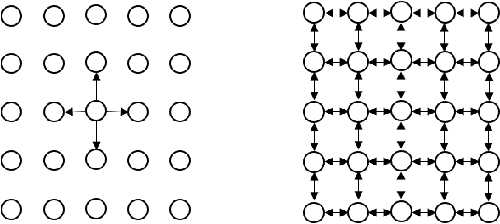

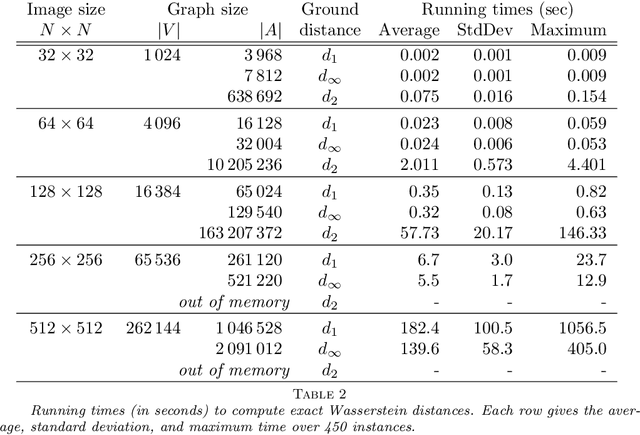
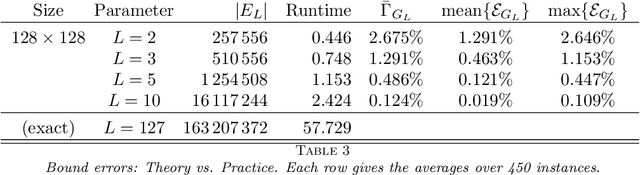
In this work, we present a method to compute the Kantorovich distance, that is, the Wasserstein distance of order one, between a pair of two-dimensional histograms. Recent works in Computer Vision and Machine Learning have shown the benefits of measuring Wasserstein distances of order one between histograms with $N$ bins, by solving a classical transportation problem on (very large) complete bipartite graphs with $N$ nodes and $N^2$ edges. The main contribution of our work is to approximate the original transportation problem by an uncapacitated min cost flow problem on a reduced flow network of size $O(N)$. More precisely, when the distance among the bin centers is measured with the 1-norm or the $\infty$-norm, our approach provides an optimal solution. When the distance amongst bins is measured with the 2-norm: (i) we derive a quantitative estimate on the error between optimal and approximate solution; (ii) given the error, we construct a reduced flow network of size $O(N)$. We numerically show the benefits of our approach by computing Wasserstein distances of order one on a set of grey scale images used as benchmarks in the literature. We show how our approach scales with the size of the images with 1-norm, 2-norm and $\infty$-norm ground distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge