Proportional infinite-width infinite-depth limit for deep linear neural networks

We study the distributional properties of linear neural networks with random parameters in the context of large networks, where the number of layers diverges in proportion to the number of neurons per layer. Prior works have shown that in the infinite-width regime, where the number of neurons per layer grows to infinity while the depth remains fixed, neural networks converge to a Gaussian process, known as the Neural Network Gaussian Process. However, this Gaussian limit sacrifices descriptive power, as it lacks the ability to learn dependent features and produce output correlations that reflect observed labels. Motivated by these limitations, we explore the joint proportional limit in which both depth and width diverge but maintain a constant ratio, yielding a non-Gaussian distribution that retains correlations between outputs. Our contribution extends previous works by rigorously characterizing, for linear activation functions, the limiting distribution as a nontrivial mixture of Gaussians.

Feature learning in finite-width Bayesian deep linear networks with multiple outputs and convolutional layers

Deep linear networks have been extensively studied, as they provide simplified models of deep learning. However, little is known in the case of finite-width architectures with multiple outputs and convolutional layers. In this manuscript, we provide rigorous results for the statistics of functions implemented by the aforementioned class of networks, thus moving closer to a complete characterization of feature learning in the Bayesian setting. Our results include: (i) an exact and elementary non-asymptotic integral representation for the joint prior distribution over the outputs, given in terms of a mixture of Gaussians; (ii) an analytical formula for the posterior distribution in the case of squared error loss function (Gaussian likelihood); (iii) a quantitative description of the feature learning infinite-width regime, using large deviation theory. From a physical perspective, deep architectures with multiple outputs or convolutional layers represent different manifestations of kernel shape renormalization, and our work provides a dictionary that translates this physics intuition and terminology into rigorous Bayesian statistics.

Inversion dynamics of class manifolds in deep learning reveals tradeoffs underlying generalisation

To achieve near-zero training error in a classification problem, the layers of a deep network have to disentangle the manifolds of data points with different labels, to facilitate the discrimination. However, excessive class separation can bring to overfitting since good generalisation requires learning invariant features, which involve some level of entanglement. We report on numerical experiments showing how the optimisation dynamics finds representations that balance these opposing tendencies with a non-monotonic trend. After a fast segregation phase, a slower rearrangement (conserved across data sets and architectures) increases the class entanglement. The training error at the inversion is remarkably stable under subsampling, and across network initialisations and optimisers, which characterises it as a property solely of the data structure and (very weakly) of the architecture. The inversion is the manifestation of tradeoffs elicited by well-defined and maximally stable elements of the training set, coined "stragglers", particularly influential for generalisation.

Beyond the storage capacity: data driven satisfiability transition

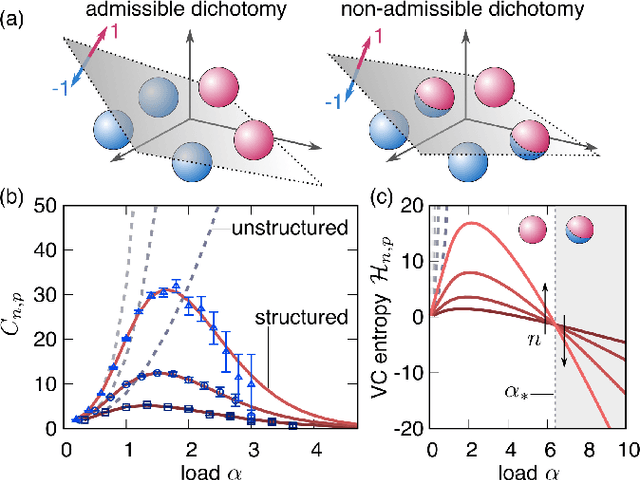
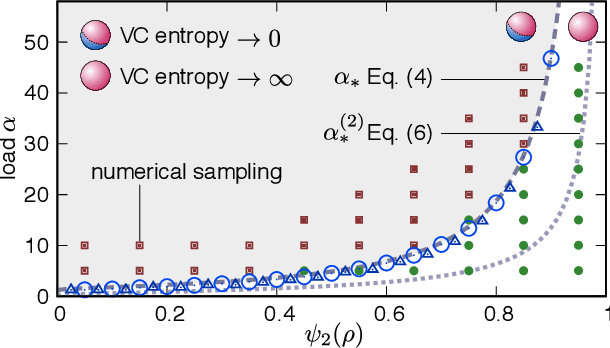
Data structure has a dramatic impact on the properties of neural networks, yet its significance in the established theoretical frameworks is poorly understood. Here we compute the Vapnik-Chervonenkis entropy of a kernel machine operating on data grouped into equally labelled subsets. At variance with the unstructured scenario, entropy is non-monotonic in the size of the training set, and displays an additional critical point besides the storage capacity. Remarkably, the same behavior occurs in margin classifiers even with randomly labelled data, as is elucidated by identifying the synaptic volume encoding the transition. These findings reveal aspects of expressivity lying beyond the condensed description provided by the storage capacity, and they indicate the path towards more realistic bounds for the generalization error of neural networks.

Intrinsic dimension estimation for locally undersampled data

High-dimensional data are ubiquitous in contemporary science and finding methods to compress them is one of the primary goals of machine learning. Given a dataset lying in a high-dimensional space (in principle hundreds to several thousands of dimensions), it is often useful to project it onto a lower-dimensional manifold, without loss of information. Identifying the minimal dimension of such manifold is a challenging problem known in the literature as intrinsic dimension estimation (IDE). Traditionally, most IDE algorithms are either based on multiscale principal component analysis (PCA) or on the notion of correlation dimension (and more in general on k-nearest-neighbors distances). These methods are affected, in different ways, by a severe curse of dimensionality. In particular, none of the existing algorithms can provide accurate ID estimates in the extreme locally undersampled regime, i.e. in the limit where the number of samples in any local patch of the manifold is less than (or of the same order of) the ID of the dataset. Here we introduce a new ID estimator that leverages on simple properties of the tangent space of a manifold to overcome these shortcomings. The method is based on the full correlation integral, going beyond the limit of small radius used for the estimation of the correlation dimension. Our estimator alleviates the extreme undersampling problem, intractable with other methods. Based on this insight, we explore a multiscale generalization of the algorithm. We show that it is capable of (i) identifying multiple dimensionalities in a dataset, and (ii) providing accurate estimates of the ID of extremely curved manifolds. In particular, we test the method on manifolds generated from global transformations of high-contrast images, relevant for invariant object recognition and considered a challenge for state-of-the-art ID estimators.

Counting the learnable functions of structured data

Cover's function counting theorem is a milestone in the theory of artificial neural networks. It provides an answer to the fundamental question of determining how many binary assignments (dichotomies) of $p$ points in $n$ dimensions can be linearly realized. Regrettably, it has proved hard to extend the same approach to more advanced problems than the classification of points. In particular, an emerging necessity is to find methods to deal with structured data, and specifically with non-pointlike patterns. A prominent case is that of invariant recognition, whereby identification of a stimulus is insensitive to irrelevant transformations on the inputs (such as rotations or changes in perspective in an image). An object is therefore represented by an extended perceptual manifold, consisting of inputs that are classified similarly. Here, we develop a function counting theory for structured data of this kind, by extending Cover's combinatorial technique, and we derive analytical expressions for the average number of dichotomies of generically correlated sets of patterns. As an application, we obtain a closed formula for the capacity of a binary classifier trained to distinguish general polytopes of any dimension. These results may help extend our theoretical understanding of generalization, feature extraction, and invariant object recognition by neural networks.