Beyond the storage capacity: data driven satisfiability transition
Paper and Code
May 20, 2020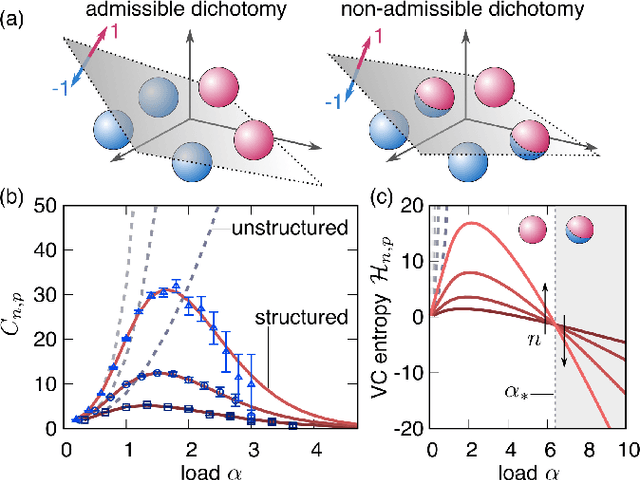
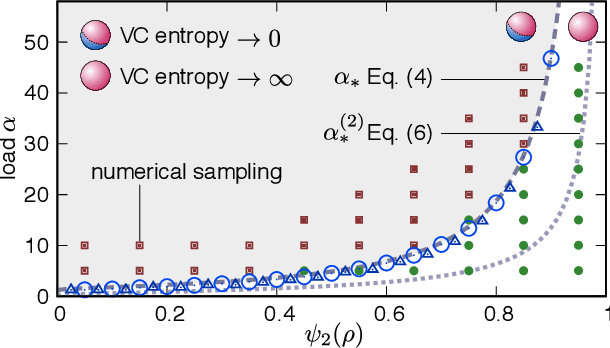
Data structure has a dramatic impact on the properties of neural networks, yet its significance in the established theoretical frameworks is poorly understood. Here we compute the Vapnik-Chervonenkis entropy of a kernel machine operating on data grouped into equally labelled subsets. At variance with the unstructured scenario, entropy is non-monotonic in the size of the training set, and displays an additional critical point besides the storage capacity. Remarkably, the same behavior occurs in margin classifiers even with randomly labelled data, as is elucidated by identifying the synaptic volume encoding the transition. These findings reveal aspects of expressivity lying beyond the condensed description provided by the storage capacity, and they indicate the path towards more realistic bounds for the generalization error of neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge