Ioannis Kosmidis
Scalable and Interpretable Marked Point Processes
May 30, 2021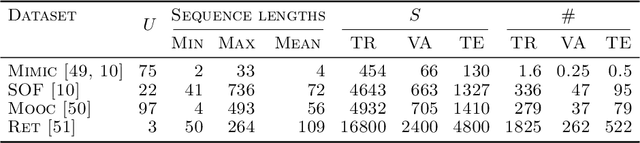
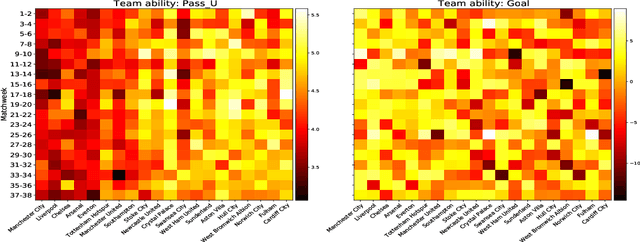
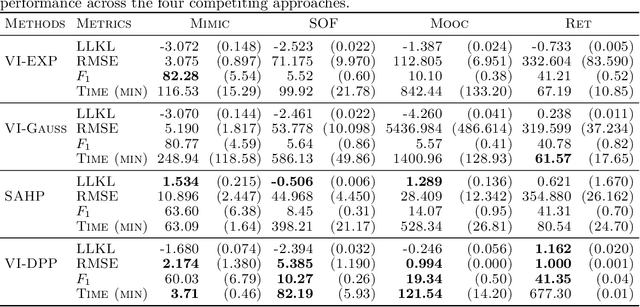
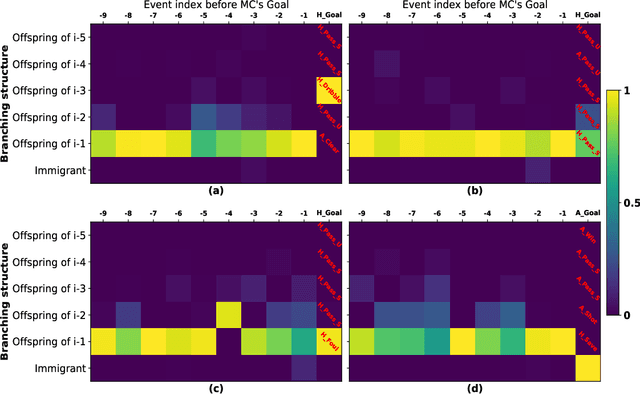
Abstract:We introduce a novel inferential framework for marked point processes that enjoys both scalability and interpretability. The framework is based on variational inference and it aims to speed up inference for a flexible family of marked point processes where the joint distribution of times and marks can be specified in terms of the conditional distribution of times given the process filtration, and of the conditional distribution of marks given the process filtration and the current time. We assess the predictive ability of our proposed method over four real-world datasets where results show its competitive performance against other baselines. The attractiveness of our framework for the modelling of marked point processes is illustrated through a case study of association football data where scalability and interpretability are exploited for extracting useful informative patterns.
Modeling outcomes of soccer matches
Aug 03, 2018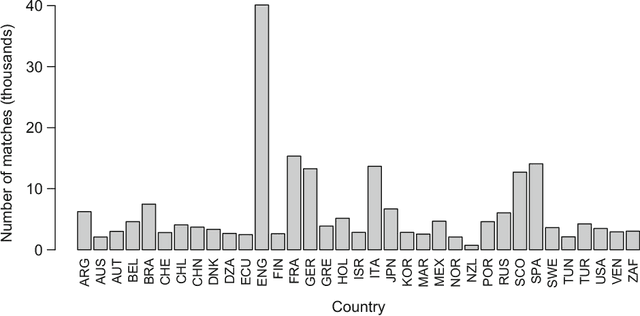
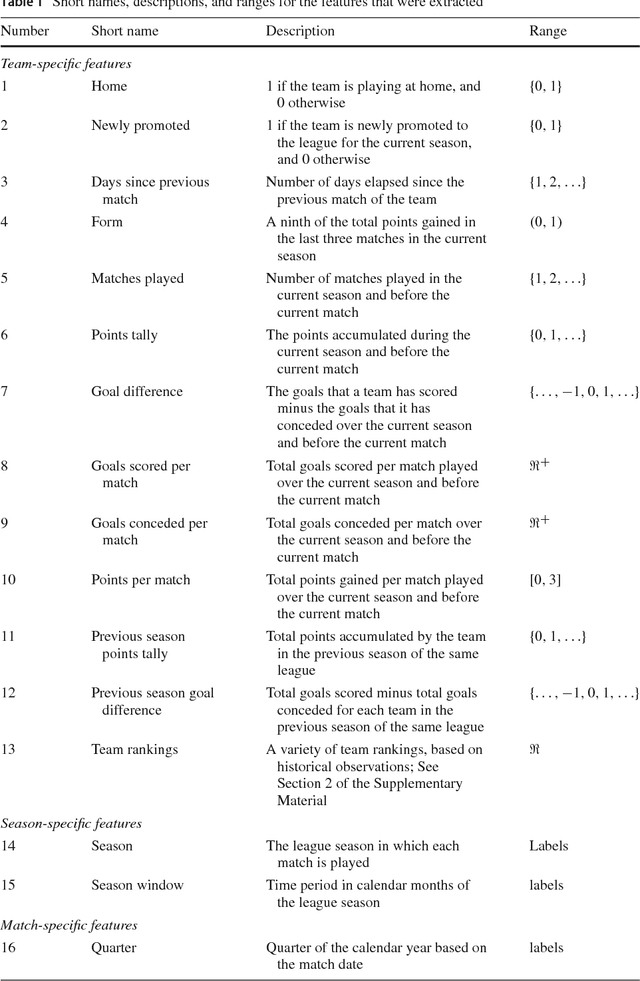
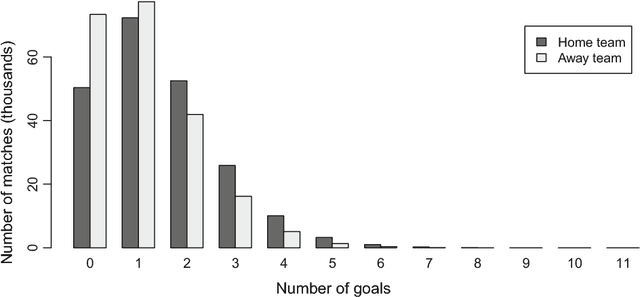
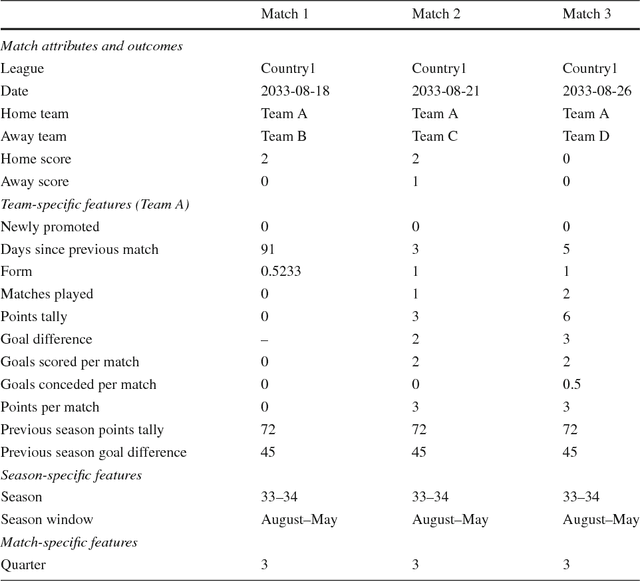
Abstract:We compare various extensions of the Bradley-Terry model and a hierarchical Poisson log-linear model in terms of their performance in predicting the outcome of soccer matches (win, draw, or loss). The parameters of the Bradley-Terry extensions are estimated by maximizing the log-likelihood, or an appropriately penalized version of it, while the posterior densities of the parameters of the hierarchical Poisson log-linear model are approximated using integrated nested Laplace approximations. The prediction performance of the various modeling approaches is assessed using a novel, context-specific framework for temporal validation that is found to deliver accurate estimates of the test error. The direct modeling of outcomes via the various Bradley-Terry extensions and the modeling of match scores using the hierarchical Poisson log-linear model demonstrate similar behavior in terms of predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge