Modeling outcomes of soccer matches
Paper and Code
Aug 03, 2018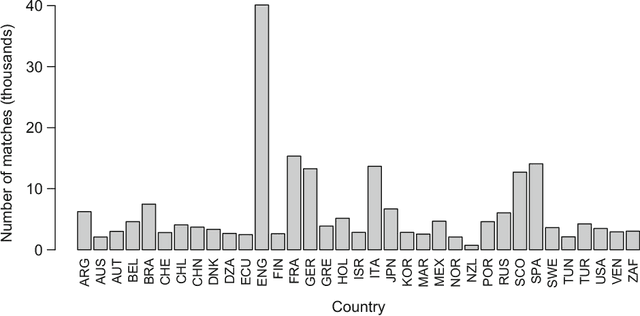
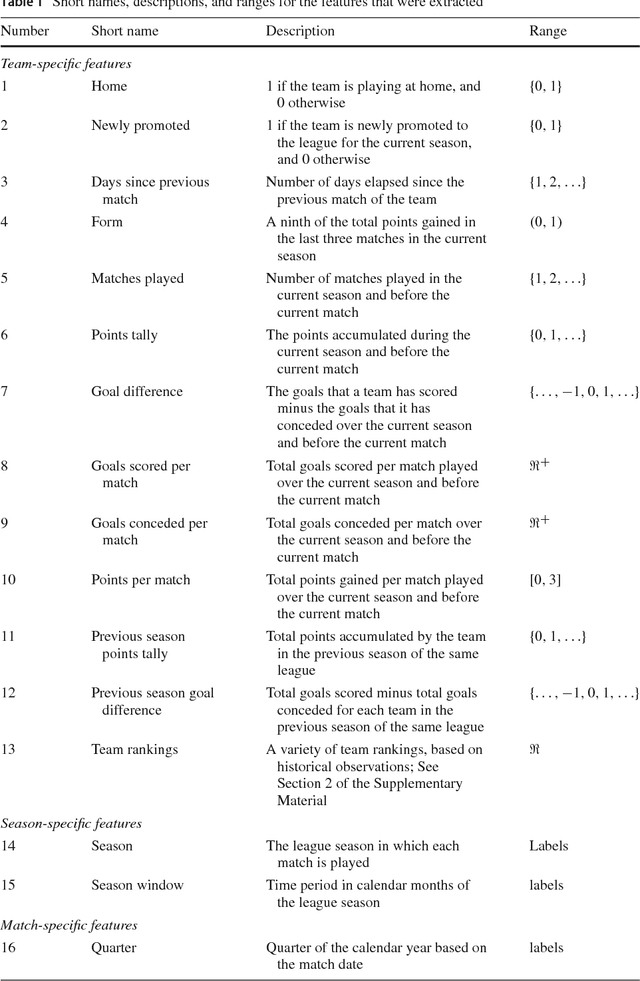
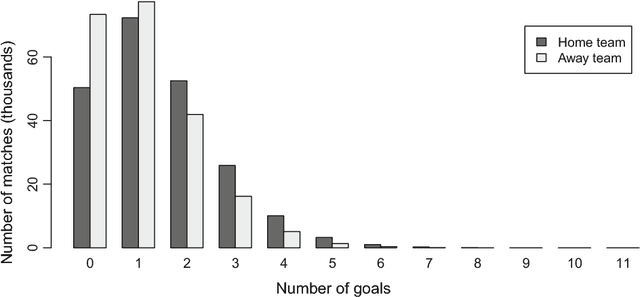
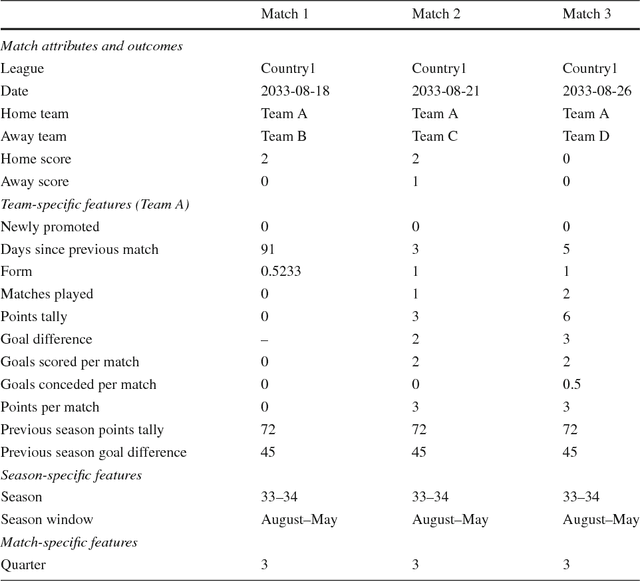
We compare various extensions of the Bradley-Terry model and a hierarchical Poisson log-linear model in terms of their performance in predicting the outcome of soccer matches (win, draw, or loss). The parameters of the Bradley-Terry extensions are estimated by maximizing the log-likelihood, or an appropriately penalized version of it, while the posterior densities of the parameters of the hierarchical Poisson log-linear model are approximated using integrated nested Laplace approximations. The prediction performance of the various modeling approaches is assessed using a novel, context-specific framework for temporal validation that is found to deliver accurate estimates of the test error. The direct modeling of outcomes via the various Bradley-Terry extensions and the modeling of match scores using the hierarchical Poisson log-linear model demonstrate similar behavior in terms of predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge